How much water? (Mathathon Problem 1)
Dream is a Minecraft speed-runner. For those of you who don't know what this means, he tries to beat the game Minecraft, as fast as possible.
Now, while playing the video game, he often finds himself falling from a high place, and needs a bucket of water to save himself. That is why, he has a stash of frustum-shaped buckets in his home at all times.
Dream's bucket
While he is on a mountain, exploring the game, he finds a lake. He knows its a good time to get water, so he gets his bucket out. He is also a avid thinker, so he wonders how much water will fit inside the bucket, if it is filled up completely.
He knows the following information -
-
His bucket's radius at the bottom is 4 0 c m
-
His bucket's radius at the top is 7 0 c m
-
His bucket's height is 7 0 c m
-
A liter is equal to a thousand centimeter cubed
Can he find the the volume of water that he can fit inside the bucket? If yes, then give the volume of water, if no, then give your answer as 0 .
( π ≈ 7 2 2 )
The answer is 682.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
I used two different methods to obtain the answer.
The first one uses the volume of a cone in cm³.

I will try to remake it with bigger text, I couldn't use another definition because of the limit of the files...
The second one uses the volume of solids of revolution and is in dm³.
This method uses an integral to calculate the volume of a function in rotation around the axis.

I really want to give you bonus points for dream, but that would be unfair lmao
| Accuracy | 5/5 | Answer and assumptions are correct |
| Readability | 5/5 | Perfect use of Gif |
| Ingenuity | 4/5 | Integral approach shown clearly with co-ordinate system |
| Total | 14/15 | Marvellous! Keep it up!! |
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Animations are clear and concise |
| Ingenuity | 4/5 | Integral approach shown very well |
| Total | 14/15 | Great job! I will update your score on the members and points note! |
I will explain why the volume of the frustum is approximately 682 litres using integrals. The main approach will be to think of it as being constructed out of many, many thin cylinders and then just take the sum of the volumes of these cylinders as their height d h approaches zero.
V = ∫ d V , where d V is one of those cylinders. The general formula for the volume of a cylinder is V = π r 2 ⋅ h . Therefore d V = π r 2 d h . However, r is not constant, but grows linearly as the height increases. Using the general formula for a linear function and two known points, r ( h ) = 4 0 + 7 0 7 0 − 4 0 h = 4 0 + 7 0 3 0 h .
Pluggin the expression for d V and r into the integral, we find that V = ∫ 0 7 0 π r 2 d h = π ∫ 0 7 0 4 0 2 + 7 0 2 ⋅ 3 0 ⋅ 4 0 h + 7 0 2 3 0 2 h 2 d h . Which is of course V = π [ 4 0 2 ⋅ 7 0 + 7 0 3 0 ⋅ 4 0 ⋅ 7 0 2 + 3 ⋅ 7 0 2 3 0 2 7 0 3 ] ≈ 6 8 1 7 2 5 . 6 1 c m 3 . Noting that we have unit c m 3 , we will divide by 1000 to simplify and yield a volume in litres, which is our final result and thus V ≈ 6 8 1 . 7 3 d m 3 ≈ 6 8 2 l
You can easily derive the general formula using the same method. Just substitute 7 0 = R , 4 0 = r , 7 0 = h et voilà!
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Proper latex has been used and I really like how you explained the integral at the top |
| Ingenuity | 4/5 | Genius, using integrals instead of the normal frustum formula, though a tiny bit tedious |
| Total | 14/15 | Amazing! I will update your score on the members and points note! |
| Accuracy | 5/5 | Answer and assumptions are correct |
| Readability | 4/5 | Possible to reduce some terms so that the final integral doesn’t look too ugly (or should have replaced with R,r and h and substituted in the end) |
| Ingenuity | 4/5 | For the integral approach, should have done a bit more on how the π r 2 d h part came (maybe by using a picture) |
| Total | 13/15 | Amazing! |
The bucket is in the shape of a frustum as specified in the question.
Volume of a frustum = 1 / 3 × π × h ( R 2 + r 2 + R × r )
where h is the height of the frustum, r is the bottom radius and R is the top radius.
Volume of the bucket = 1 / 3 × 2 2 / 7 × 7 0 ( 7 0 2 + 4 0 2 + 7 0 × 4 0 ) = 2 1 2 2 × 7 0 × ( 4 9 0 0 + 1 6 0 0 + 2 8 0 0 ) = 2 1 2 2 × 7 0 × 9 3 0 0 = 6 8 2 0 0 0 c m 3
Since 1 L = 1000cm^3
Volume in litres = 1 0 0 0 6 8 2 0 0 0
6 8 2 L
Aditya Mittal
| Accuracy | 5/5 | Answer and assumptions are correct |
| Readability | 5/5 | Its clearly done |
| Ingenuity | 0/5 | Giving a link to a solution not done by you doesn’t count |
| Total | 10/15 | Good job! |
Byjus
| Accuracy | 5/5 | Answer and assumptions are correct |
| Readability | -4/5 | Cant even read some parts of the solution |
| Ingenuity | 2/5 | Proved the formula |
| Total | 3/15 | Bad job?! Try getting double digits next time |
Log in to reply
lmao so true...
I agree with the points given but 5 − 3 + 2 = 4
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Everything is clear and readable |
| Ingenuity | 0/5 | Common Approach, byju link doesn't count |
| Total | 10/15 | Great job! I will update your score on the members and points note! |
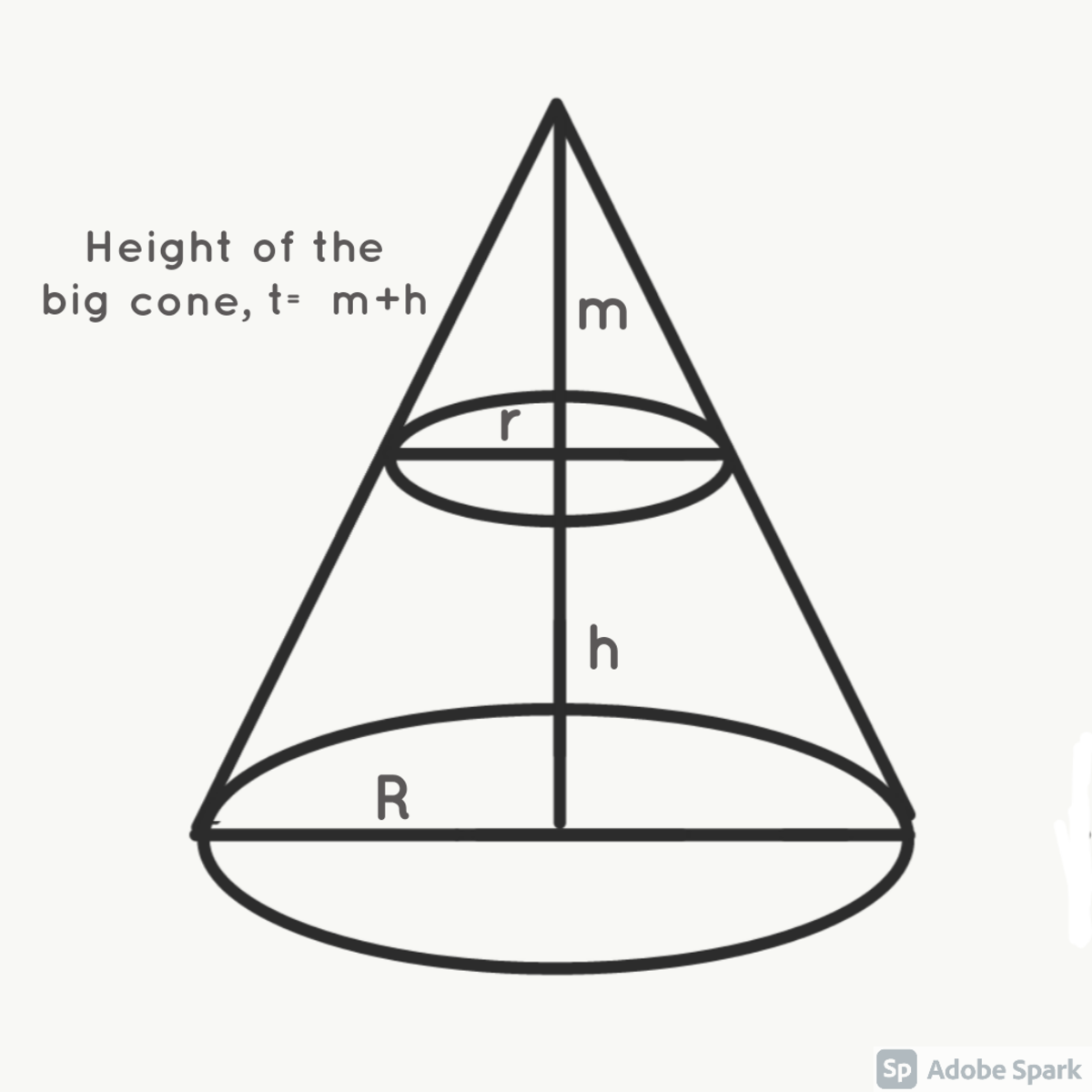
Given that the volume of a cone is given by 3 1 π a 2 b where a is the radius of the cone and b is its perpendicular height. For a frustum of a cone as shown above, we can generalize its volume to be,
Volume of the larger cone- Volume of the smaller cone
3 1 π R 2 t − 3 1 π r 2 m
Putting t = h + m
3 1 π R 2 h + 3 1 π R 2 m − 3 1 π r 2 m
3 1 π R 2 h + 3 1 π m ( R 2 − r 2 )
Remember that in both the upper and the lower cone the triangles made by radii, respective perpendicular heights and slant heights (hypotenuses) must be similar triangles here, i.e,
r m = R h + m provides m = R − r h r
Putting the value of m we just got in the equation above we have,
3 1 π R 2 h + 3 1 π ( R − r h r ) ( R 2 − r 2 )
Since R 2 − r 2 = ( R + r ) ( R − r ) , we get
3 1 π R 2 h + 3 1 π ( h r ) ( R + r )
And finally the volume of a frustum of a cone,
3 1 π h ( R 2 + r 2 + R r )
Here we have R = 7 0 c m , r = 4 0 c m , h = 7 0 c m , which gives volume from the formula,
3 1 π ( 7 0 ) ( ( 7 0 ) 2 + ( 4 0 ) 2 + ( 7 0 × 4 0 ) ) ≈ 6 8 2 0 0 0 c m 3
Since 1 0 0 0 c m 3 = 1 litre we get, the volume of the frustum, 6 8 2 litres
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Proper latex has been used and good use of image to show formula |
| Ingenuity | 3/5 | Common Approach, but formula has been proven |
| Total | 13/15 | Great job! I will update your score on the members and points note! |
Log in to reply
I would have never tried solving for the formula, thanks
| Accuracy | 5/5 | Answer and assumptions are correct |
| Readability | 5/5 | Good use of latex |
| Ingenuity | 2/5 | Proved the formula using formula for volume of cone |
| Total | 12/15 | Great job! |
The shape of the bucket is frustum ∴ V o l u m e = 3 1 π × h e i g h t ( b o t t o m c i r c l e ′ s r a d i u s 2 + t o p c i r c l e ′ s r a d i u s 2 + t o p c i r c l e ′ s r a d i u s × b o t t o m c i r c l e ′ s r a d i u s ) = 3 1 × 7 2 2 × 7 0 c m ( 7 0 2 c m 2 + 4 0 2 c m 2 + 7 0 ∗ 4 0 c m 2 ) = 3 2 2 × 1 0 × 1 0 2 × ( 7 2 + 4 2 + 7 × 4 ) c m 3 = 3 2 2 × [ ( 7 + 4 ) 2 − 7 × 4 ] × 1 0 3 c m 3 = 3 2 2 × [ 1 1 2 − 2 8 ] × L = 3 2 2 × [ 1 2 1 − 2 8 ] × L = 3 2 2 × 9 3 × L = 3 2 2 × 3 × 3 1 × L = 2 2 × 3 1 L = 6 8 2 L
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Proper latex has been used |
| Ingenuity | 0/5 | Common Approach |
| Total | 10/15 | Great job! I will update your score on the members and points note! |
| Accuracy | 5/5 | Answer and assumptions are correct |
| Readability | 5/5 | Working out has been done perfectly |
| Ingenuity | 1/5 | Used a 2 + b 2 + a b = ( a + b ) 2 − a b to simplify calculations(in a way) |
| Total | 11/15 | Great job! 628 has to be changed to 682 though |
Most Common Solution -
Volume of frustum = 3 π h ( ( r 1 ) 2 + ( r 2 ) 2 + r 1 r 2 )
⇒ 3 ( 7 ) 2 2 ( 7 0 ) ( ( 4 0 ) 2 + ( 7 0 ) 2 + ( 4 0 ) ( 7 0 ) ) = 2 1 ( 1 5 4 0 ) ( 9 3 0 0 ) = 2 1 1 4 3 2 2 0 0 0 = 6 8 2 0 0 0 cm 3
6 8 2 0 0 0 cm 3 = 6 8 2 L
Ingenuity points if you prove the formula :)
I actually didn’t know this formula, I had to solve it from cone anyways lol
Log in to reply
lol I learnt this formula a few years ago, I just randomly remembered it and decided to make a Minecraft problem on it, coz I was watching minecraft on yt :P
Please notify me if any more solutions come on this problem
Of course one also has to substitute 22/7 for the value of pi
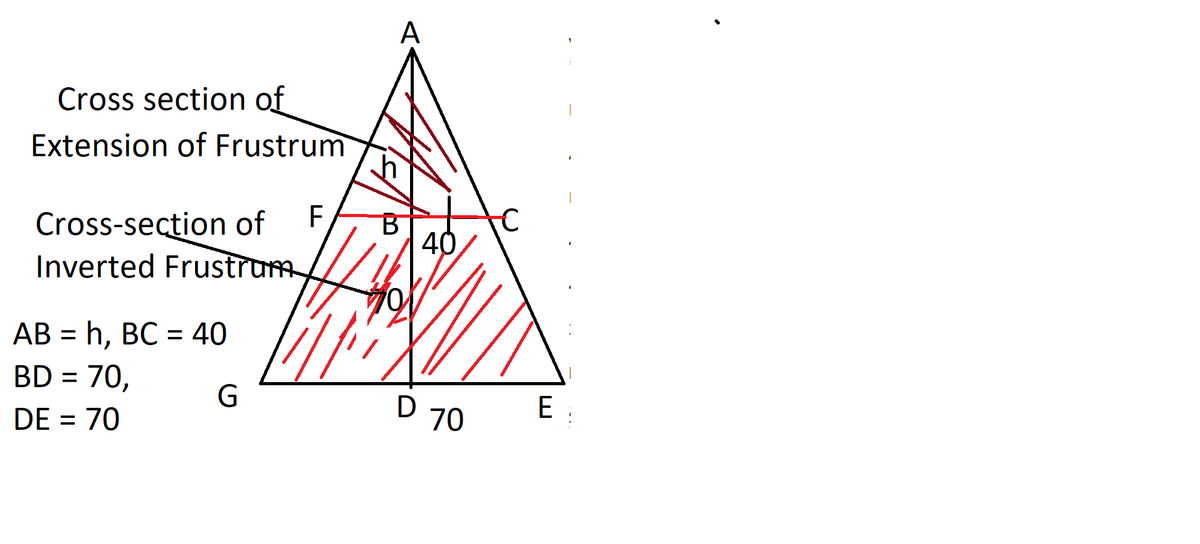
More generally, in the above, if we let BC = r, DE = R, AB = x and BD = h, we get volume of frustrum = Vol (Cone ADE) - Vol (Cone ABC)
= pi * R^2(x+h) / 3 - pi * r^2*x/3.....(1)
Now since ABC similar to ADE, we have
R/r = (x+h)/x .
(R-r)/r = (x+h-x)/x
Therefore (R-r)/r = h/x.
After algebraic manipulation, we get x = (hr) / (R - r) ....(2)
Plugging in these values in (1), we get
Vol(frustrum) = pi * R^2[h + (hr)/(R-r)] /3 - pi * r^2(hr/(R-r))/3
= pi * R^2/3[(hR - hr + hr)/(R-r)] - pi * r^2/3[hr/(R-r)]
= (pi / 3) * [hR^3]/(R-r) - (pi / 3) * hr^3 / (R-r)
= (pi / 3) * h * [(R^3 - r^3) / (R - r) ] = (pi / 3) * h * (R^2 + r^2 + Rr) .... which is the formula for volume of a frustrum of cone.... (Using the formula ...(a^3 - b^3) = (a - b) (a^2 + ab + b^2) )
(Here,) Frustum is a part of a cone which we get if we cut a cone in a plane parallel to the base.
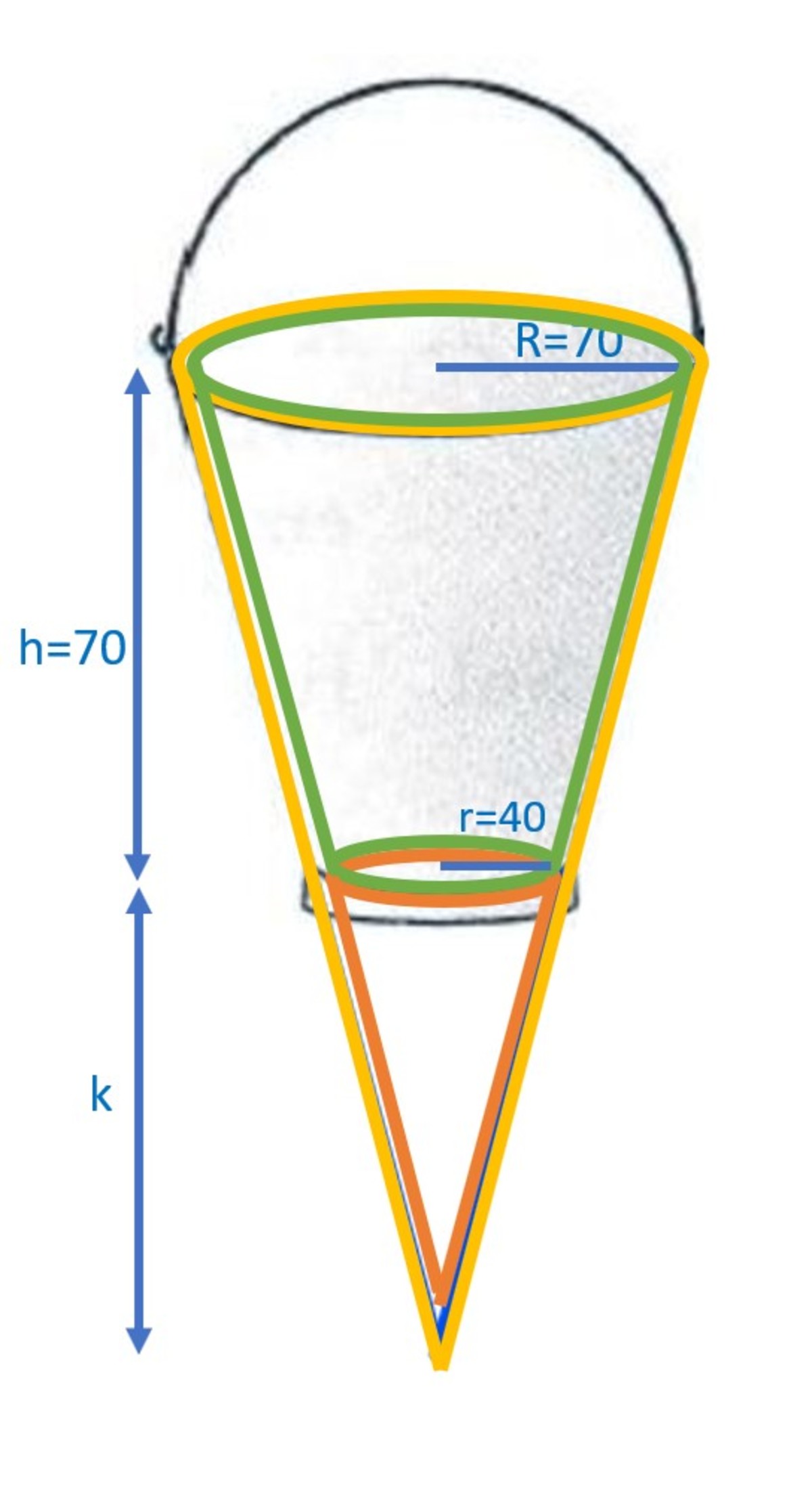
- Consider the g r e e n f r u s t u m :
Volume = Volume( y e l l o w c o n e ) - Volume( o r a n g e c o n e )
Volume of Cone = 3 1 * π (radius of base )( perpendicular height )
Volume of g r e e n f r u s t u m
= 3 π R 2 ( h + k ) - 3 π r 2 k
= 3 π * (70^2 * 70 + 70^2 k - 40^2 k)
= 3 π * (70^3 + k(70^2 - 40^2))
= 3 π * (70^3 + k(70 + 40)(70 - 40)) ..... [reason: a^2 - b^2 = (a+b)(a-b)]
= 3 π * (70^3 + k(110)(30)) ----(eqn1)
we have to find the value of 'k'
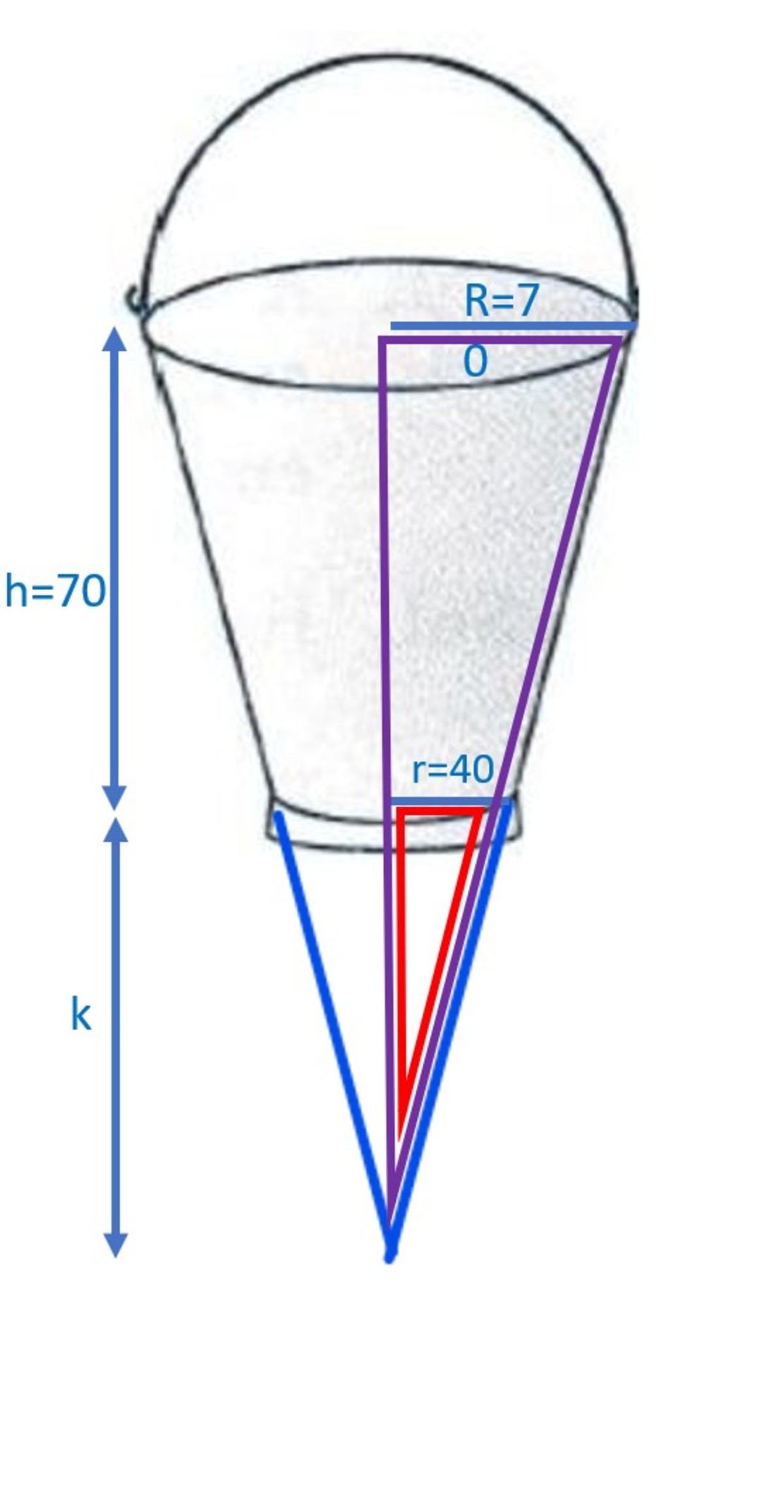
- Consider the p u r p l e t r i a n g l e & r e d t r i a n g l e :
r is parallel to R .....[definition of frustum]
Therefore by Basic Proportionality Theorem , and the common angle
p u r p l e t r i a n g l e ~ r e d t r i a n g l e .....[ S-A-S test of similarity]
r k = R k + h
4 0 k = 7 0 k + 7 0
4 0 k = 7 0 k + 1
4 0 k - 7 0 k = 1
7k - 4k = 280
k = 280/3
- Substituting 'k' in (eqn1) :
Volume of g r e e n f r u s t u m = 3 π * (70^3 + 3 ( 2 8 0 ) ( 1 1 0 ) ( 3 0 ) )
Volume of g r e e n f r u s t u m = 7 ∗ 3 2 2 * 7000(49 + 44)
Volume of g r e e n f r u s t u m = 3 ( 2 2 ) ( 1 0 0 0 ) ( 9 3 )
Volume of g r e e n f r u s t u m = 682000 cm^3
1000 cm^3 = 1 liter
the bucket can hold 682 liters of water
If we substitute the values with variables then we can get the formula
| Accuracy | 5/5 | Answer and assumptions are correct |
| Readability | 5/5 | Steps are lengthy but correct |
| Ingenuity | 2/5 | Proved the formula better than byjus but a little long |
| Total | 12/15 | Epic, byjus should copy this solution rather the one they gave |
| Accuracy | 5/5 | Everything is correct |
| Readability | 5/5 | Everything is clear and readable |
| Ingenuity | 2/5 | The proof is sorta given but a bit long and tedious |
| Total | 12/15 | Great job! I will update your score on the members and points note! |
The volume of the bucket can be found by subtracting 2 cones.
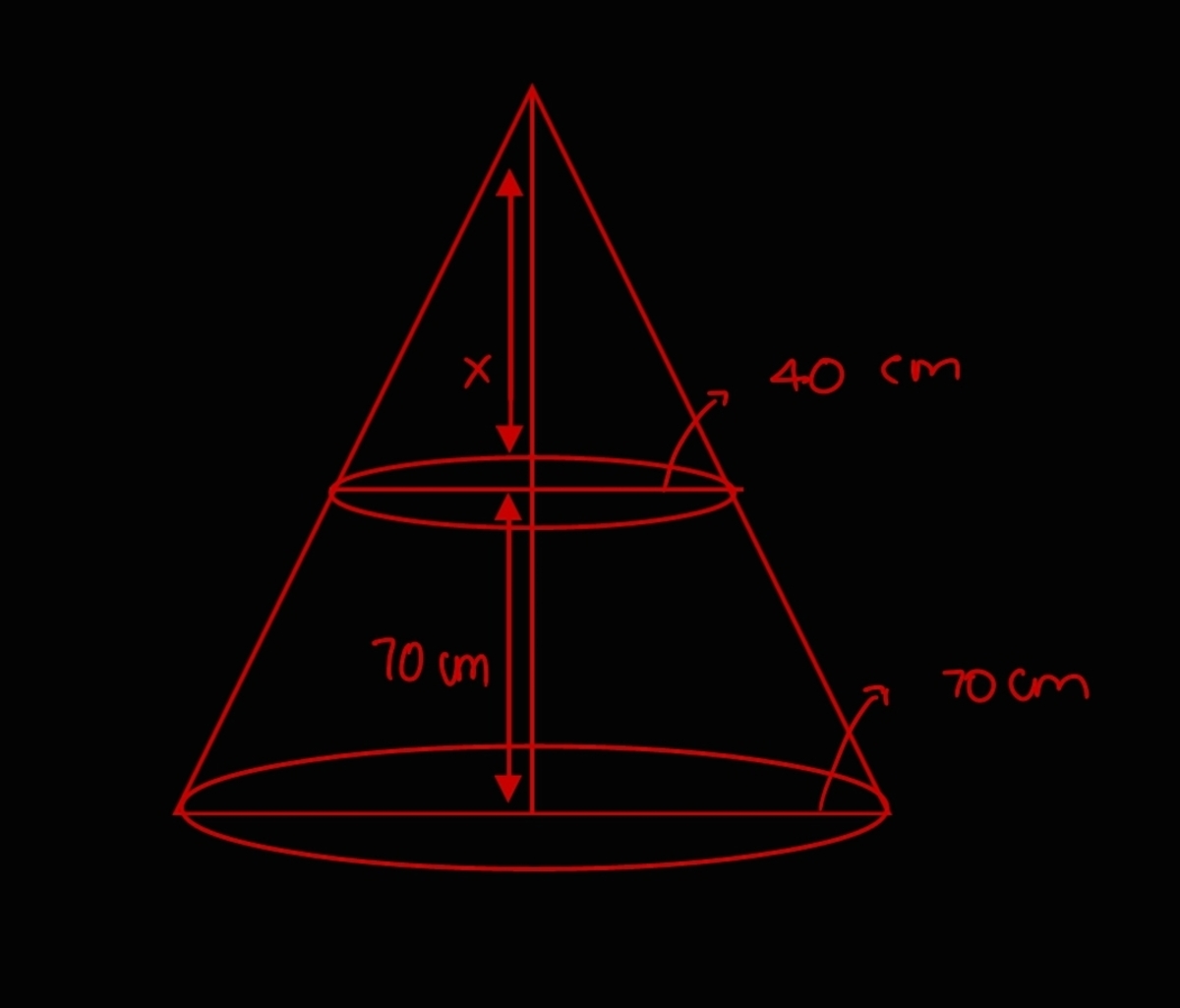 These are the 2 cones
These are the 2 cones
- First, by similarity (between the small and big cones) we get, x + 7 0 x = 7 0 4 0
- By solving the equation we get x as 3 2 8 0 cm
Volume of cone = 3 1 π r²h
Volume of bucket
- = Volume of big cone - Volume of small cone
- = 3 1 π (70)²(70+ 3 2 8 0 ) - 3 1 π (40)²( 3 2 8 0 )
- = 682000 cm³
- = 682 L
| Accuracy | 5/5 | Answer and assumptions are correct |
| Readability | 4/5 | Its readable, that’s all I can say |
| Ingenuity | 2/5 | Proved the formula |
| Total | 11/15 | Great job! Most of the calculations are missing but that’s fine |
| Accuracy | 5/5 | Everything is correct |
| Readability | 4/5 | Its readable, some calculations are missing tho |
| Ingenuity | 2/5 | The formula proof approach has been used |
| Total | 11/15 | Great job! I will update your score on the members and points note! |
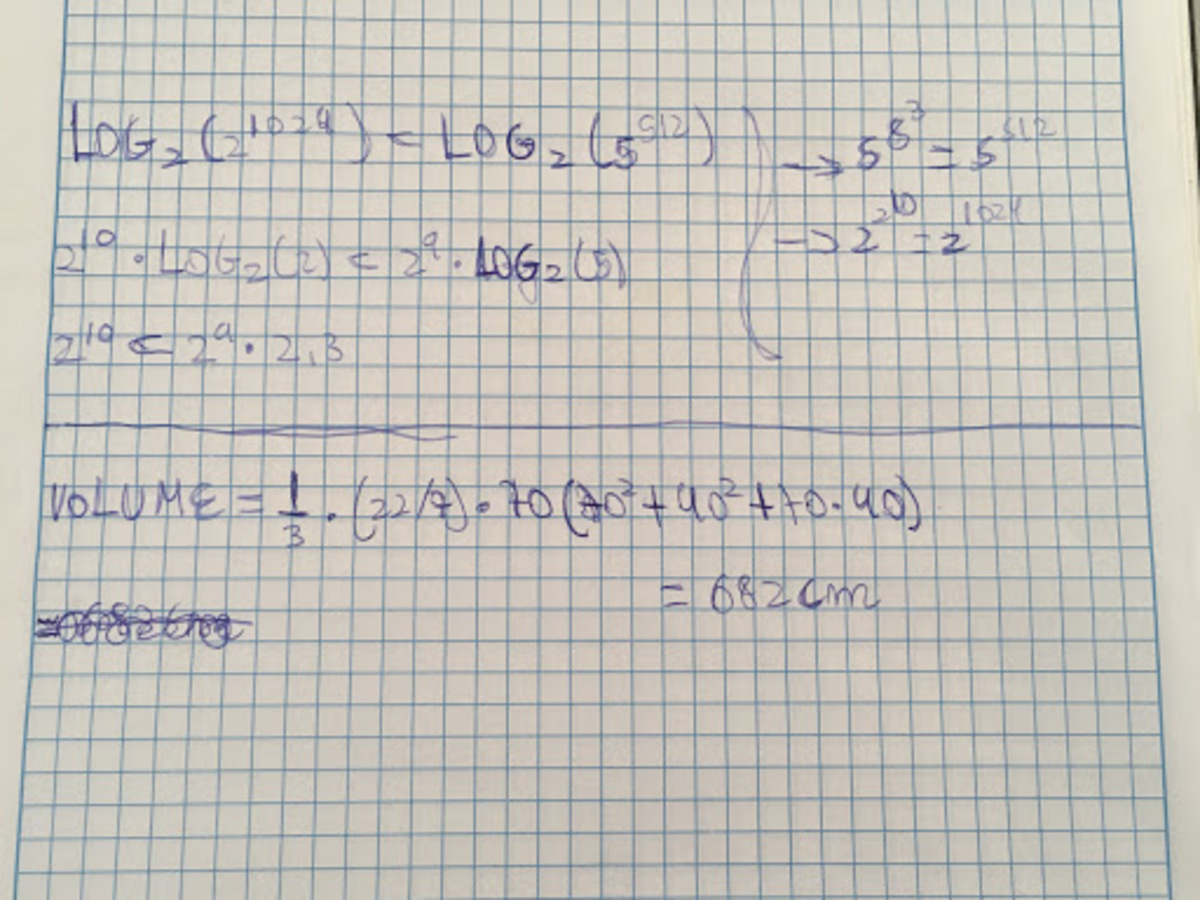
Sorry if I posted my solution to problem n. 3 is because Brilliant won't let me write my solution on that problem (and I have it correct):
@Brilliant Mathematics Please help
Hi Elijah, the system shows that you are marked correct for that problem. If you are still unable to post a solution to that problem, please let me know.
Do I get notified if I post an answer and new answers come?
No, only I get notified, but I can always mention you :)
Log in to reply
No need of that I’ll check when they come
| Accuracy | 0/5 | Assumption is wrong |
| Readability | 5/5 | Nicely quoted |
| Ingenuity | -5/5 | Answer and question have no relation |
| Total | 0/15 | Try harder next time :( (I want to copy and paste this table rather than getting it from another place) |
Log in to reply
Of course with different scores and remarks
lmao lemme do that too :P
| Accuracy | 0/5 | Assumption is wrong |
| Readability | 5/5 | Nicely quoted |
| Ingenuity | -5/5 | Answer and question have no relation |
| Total | 0/15 | Try harder next time :( (I want to copy and paste this table rather than getting it from another place) |
Log in to reply
Lmao I have achieved the impossible
hey so i entered three wrong answers so can i put my answer in a note
Log in to reply
@Percy Jackson @Kevin Long I am not very sure but I think you can only put up solutions if you got it right, but that’s upto Percy to decide
I'm sorry but you will not be allowed to give a solution if you got it wrong. @Kevin Long
Don't let anybody do that if they ask you @Jason Gomez
Log in to reply
@A Former Brilliant Member – Ok (brilliant isn’t allowing me to send short messages)
Log in to reply
@Jason Gomez – Yeah, just write (some text) after your short answer, and we'll understand. Pall Marton created the (some text) code...
@A Former Brilliant Member – why did you include the zero thing as that was one of my answers
Log in to reply
@Kevin Long – I am sorry but because you got it wrong, there is no proof that you actually even know how to solve the problem, so most will assume you just copied off another solution for points. This is why I can't let you post a solution. Also, the 0 thing is included to make it a bit tricky. If you actually tried the 0 thing, it proves you don't know the formula for the volume, so you can't post a solution.

I LOVE THE DREAM SMP!
There are many ways to look at this problem. Three good ways would be:
1. Directly calculate if you know the formula for frustum volume.
The formula for frustum volume, given bottom radius R , top radius r and height h , is V = 3 1 π h ( R 2 + r 2 + R r ) . Therefore we can plug in π ≈ 7 2 2 , h = 7 0 , R = 4 0 , r = 7 0 to find the volume (must be converted to Liters): V = 3 1 × 7 2 2 × 7 0 ( 4 0 2 + 7 0 2 + 4 0 × 7 0 = 6 8 2 0 0 0 ( cm 3 ) = 6 8 2 L .
2. Calculate difference of cones not knowing the formula for frustum volume.
Extending the cone by imagination and using similarity, we get the pic below: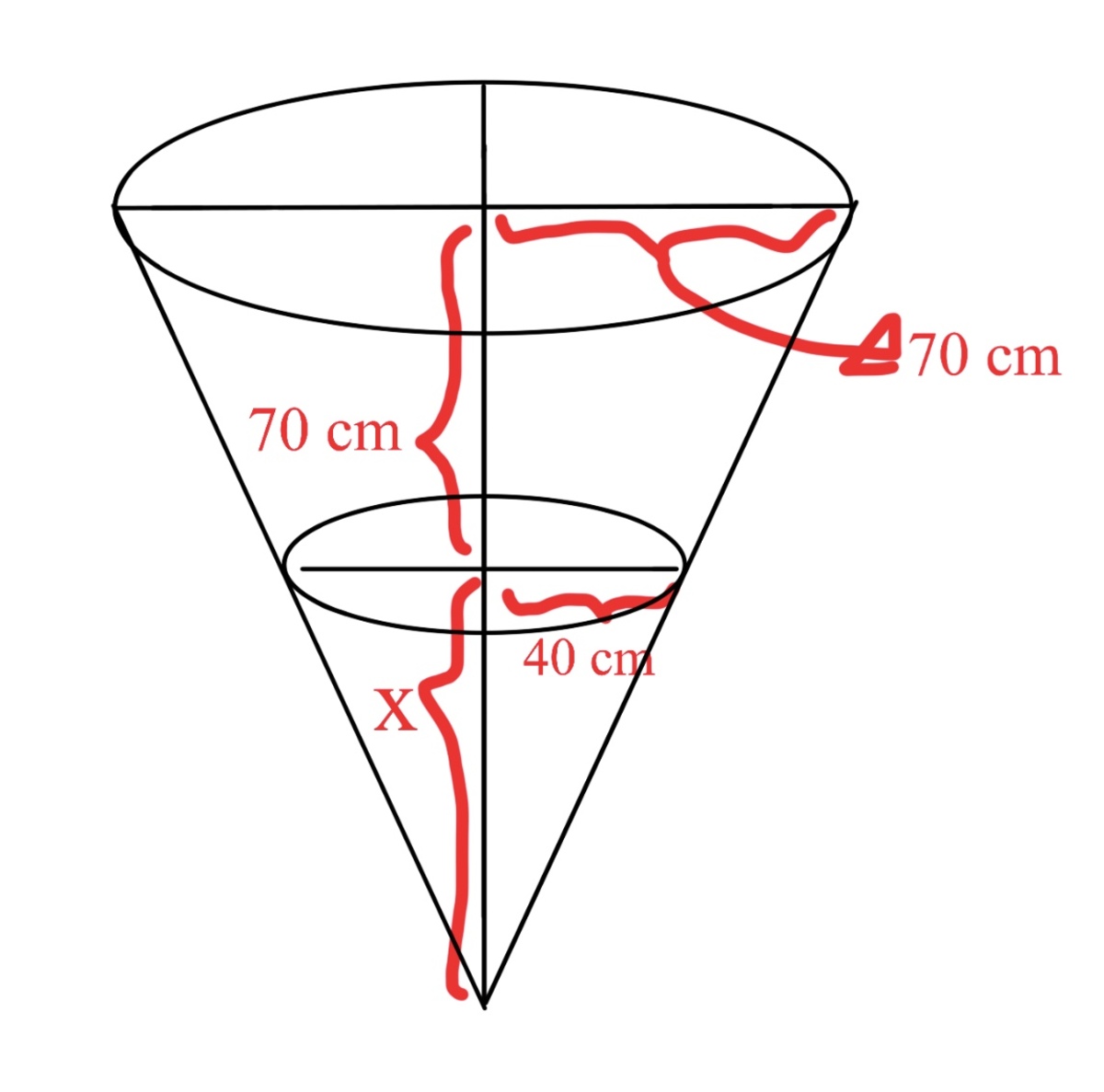 Let the height of the increased cone be
x
. By similarity, we get
x
4
0
=
7
0
+
x
7
0
. Solve this to get
x
=
3
2
8
0
.
Let the height of the increased cone be
x
. By similarity, we get
x
4
0
=
7
0
+
x
7
0
. Solve this to get
x
=
3
2
8
0
.
So the volume of the frustum is the volume of the larger cone minus the volume of the smaller cone (the formula for cone volume is 3 1 π r 2 h where r stands for bottom radius and h stands for height): V frustum = V big cone − V small cone = 3 1 π × 7 0 2 × ( 7 0 + 3 2 8 0 ) − 3 1 π × 4 0 2 × 3 2 8 0 = 6 8 2 0 0 0 ( cm 3 ) π is replaced with 3 1 here
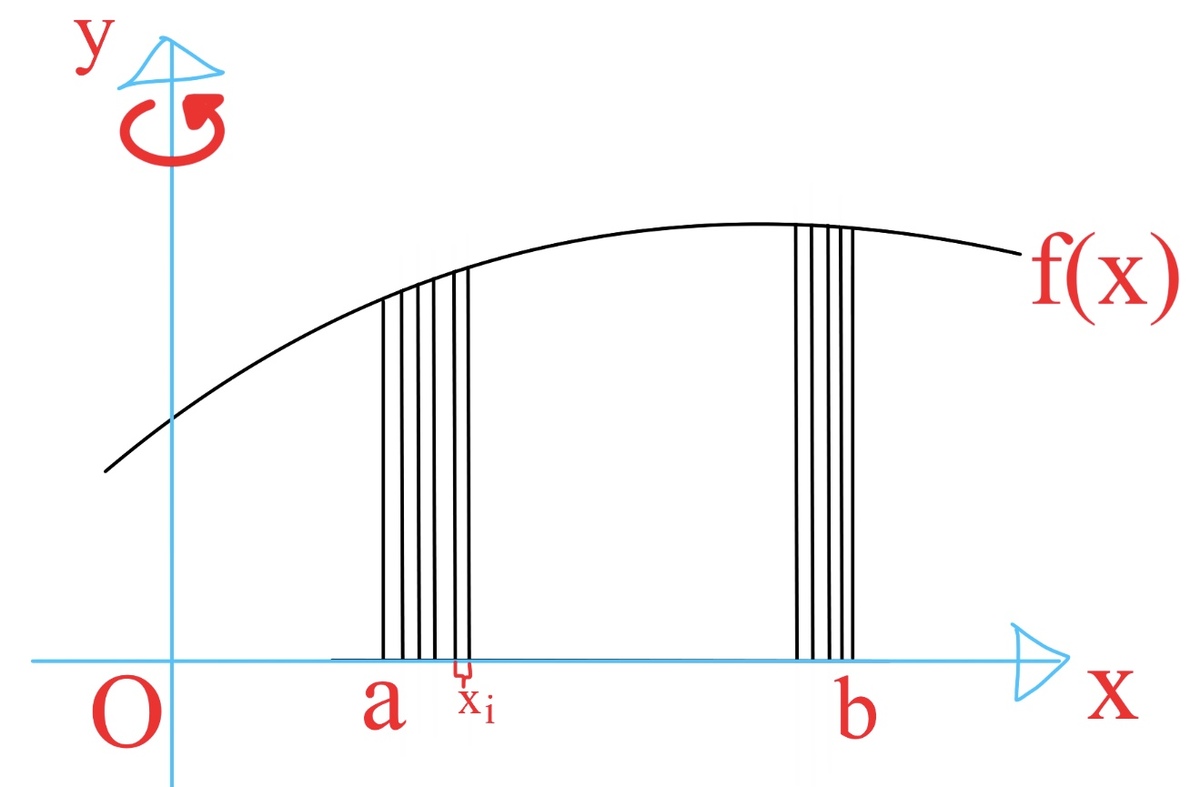
3. Use the ‘Baumkuchen’ integral.
If under 18, do NOT do at home without adult supervision to avoid brain explosion.
 Baumkuchen has log-like stripes
Explanation:
Baumkuchen has log-like stripes
Explanation:
 Here I made a little mistake when labelling :P
x
i
should be replaced with
d
x
:)
Here I made a little mistake when labelling :P
x
i
should be replaced with
d
x
:)
 I forgot the absolute value brackets :P
I forgot the absolute value brackets :P
This is mentioned in a book I read which finds volumes of 3D-shapes created by rotating the shape bounded by functions f ( x ) and g ( x ) in region a ≤ x ≤ b : V = 2 π ∫ a b ∣ x ∣ ∣ f ( x ) − g ( x ) ∣ d x . The absolute value brackets are there to make sure V is positive. THIS WORKS ONLY IF THE ROTATED BOUND IS ON THE SAME SIDE OF THE Y-AXIS.
Why is it called Baumkuchen?
It is because Baumkuchen is ‘log-like dessert’ in German, and the integral is like one!
We can split the integral into rings formed by the original bound split and rotated around the y-axis individually.
For simplicity, here I let g ( x ) = 0 . Of course this can be generalised to other functions as well, given above.
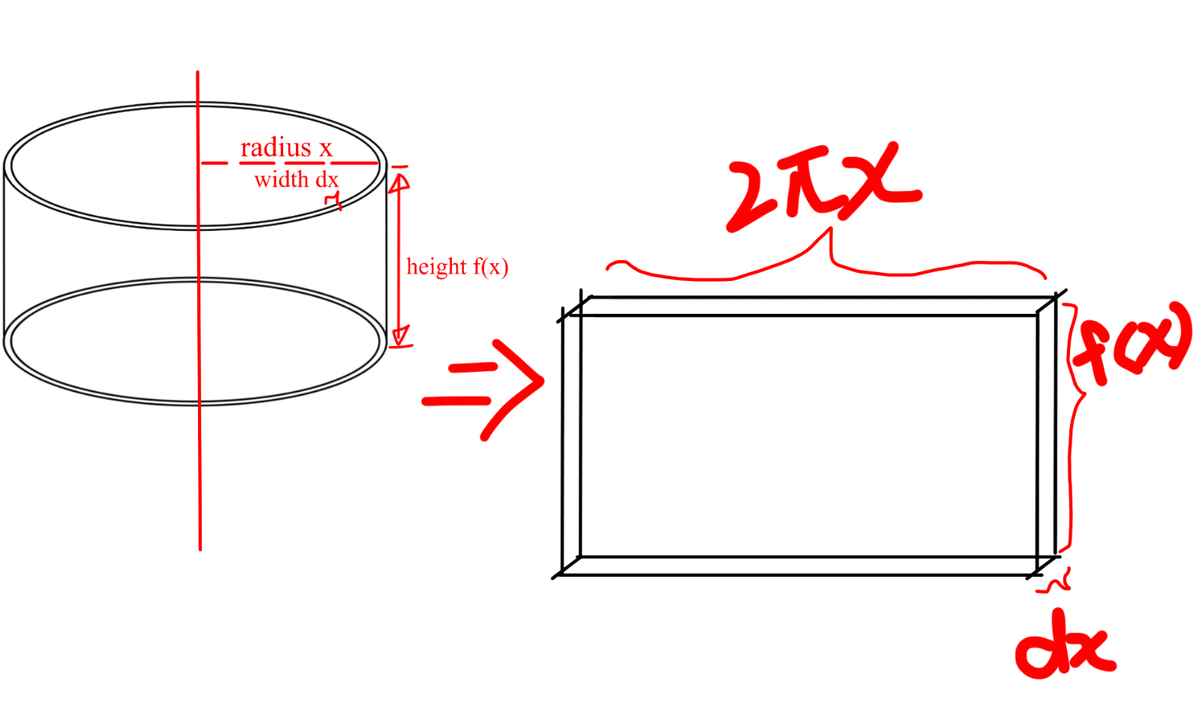
If we cut a single ‘ring’ open, we get its volume by seeing it as a cuboid:
Here the volume of the cuboid is 2 π ∣ x ∣ ∣ f ( x ) ∣ because g ( x ) = 0 and the − g ( x ) term is therefore neglected. Summing infinite cuboids gives V = 2 π ∫ a b ∣ x ∣ ∣ f ( x ) − g ( x ) ∣ d x . So we can see the frustum as a cone chopped off from another as in example 2. This way, the volume of the big cone is the integral with a = 0 , b = 7 0 , f ( x ) = 7 0 and g ( x ) = 3 7 x − 3 2 8 0 .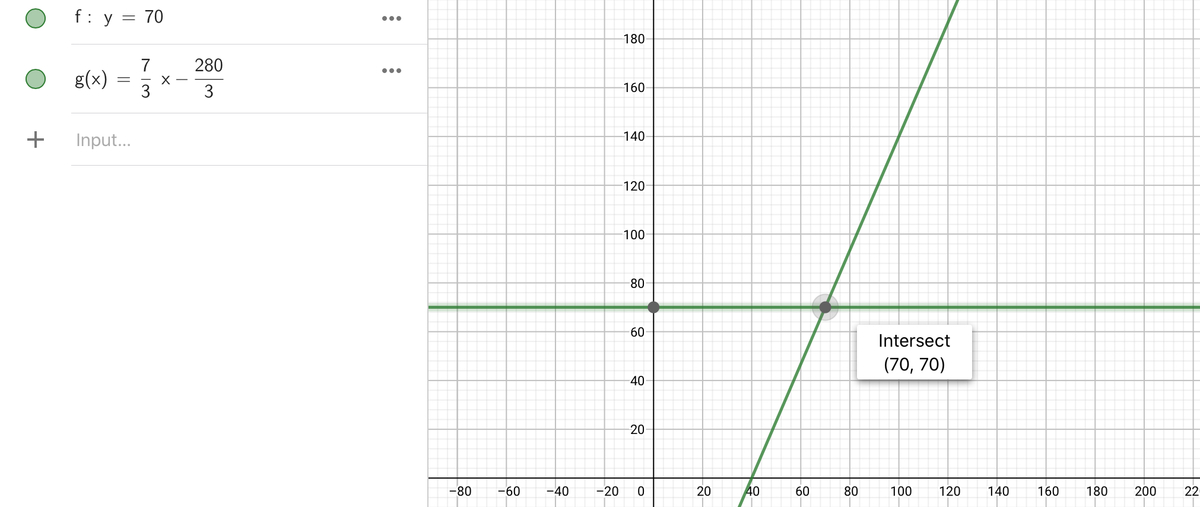 Plug in these to get
V
1
=
2
π
∫
0
7
0
∣
x
∣
∣
7
0
−
(
3
7
x
−
3
2
8
0
)
∣
=
2
π
∫
0
7
0
3
4
9
0
x
−
3
7
x
2
≈
2
×
7
2
2
(
3
2
4
5
x
2
−
9
7
x
3
∣
∣
∣
∣
0
7
0
)
=
7
5
4
6
0
0
0
9
.
Similarly we can apply the same to the small cone to get
V
2
=
9
1
8
9
4
0
0
0
.
V
1
−
V
2
=
6
2
8
0
0
0
.
Convert to liters:
6
2
8
.
Plug in these to get
V
1
=
2
π
∫
0
7
0
∣
x
∣
∣
7
0
−
(
3
7
x
−
3
2
8
0
)
∣
=
2
π
∫
0
7
0
3
4
9
0
x
−
3
7
x
2
≈
2
×
7
2
2
(
3
2
4
5
x
2
−
9
7
x
3
∣
∣
∣
∣
0
7
0
)
=
7
5
4
6
0
0
0
9
.
Similarly we can apply the same to the small cone to get
V
2
=
9
1
8
9
4
0
0
0
.
V
1
−
V
2
=
6
2
8
0
0
0
.
Convert to liters:
6
2
8
.