How quickly can you find LOVE?
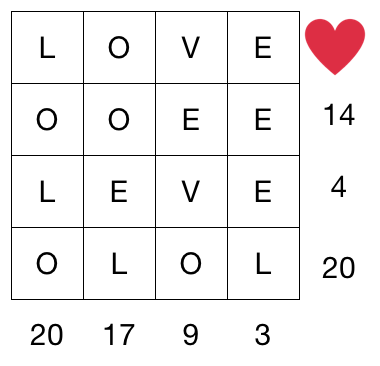 Each row and column sums up to the value on the end. What is the value of
♡
?
Each row and column sums up to the value on the end. What is the value of
♡
?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
Wish I thought of that before I could determinate de right numbers. It did helped to read your answer as a simplier approach.
Same as my way. I can't determine any of those L,O,V,E.
Log in to reply
E=1 V=2 O=8 L=0
Calvin edit: This set of values doesn't work. See solutions below to understand why "L is 3, O is 7, V is 1 and E is 0".
Log in to reply
You are wrong Tristen. L=3, E=0, O=7, & V=1.
L=0, O=8 means... It doesn't satisfy last row...??
Log in to reply
@Karthi Gopi – Looking at the solution from others, they calculated that "L is 3, O is 7, V is 1 and E is 0" instead.
Same as my way, I do not know what the values of L, O, V, E are
I now see my mistake (I can't count)
But why does this work?
Log in to reply
That's a good question. Why do you think it works?
Or, why do you think it would not work? What are your concerns?
Log in to reply
Ha! I'm a skeptic by nature, and so I have a hard time believing this actually works. So yes, I try to come up with why this might work, but I can't put my thoughts in order. Somewhere I'm having this idea that you're not adding values, but letters, and what's left is l.o.v.e. But, you need some structure there too. I notice that apart from l.o.l.o, the other columns (or rows) do not have corresponding rows (or columns). But how this connects to eachother... I find it difficult!
Log in to reply
@Pieter Breughel – Here's one way to think about it:
We are "finding the sum of 4 vertical columns". So put a * in each of these cells of a vertical column.
We are then "minus the 3 horizontal rows". So erase the * that is in each of these cells of the 3 horizontal row.
What * cells do we have left? Is there a simple description of it?
Note that we now have the sum of these * cells. Hence, what is it equivalent to?
Log in to reply
@Calvin Lin – This is what I'm getting from what you're saying: let's say we have 4 vertical columns each consisting of 4 cells. In each vertical column I put a *. In effect, we also end up having 4 horizontal rows of 4 cells. Now we remove 3 of those horizontal rows. What you're left with is one horizontal row of 4 cells where each cell contains a *.
"Is there a simple description of it? " I guess you could say (4 * 4 cells) - (3 * 4 cells).
"Note that we now have the sum of these * cells." You mean the (4 * 4 cells) - (3 * 4 cells)?
"Hence, what is it equivalent to?" I don't think I get what you're trying to say.
There's just one thing; if we use a *, like a variable, then the value of the * is the same in each cell. But here, this isn't so. Doesn't this make it "the devil in the detail"?
Log in to reply
@Pieter Breughel – Great.
The * is just meant to be a simple visual representation of the cells that you are adding up (rather than resorting to saying "Add the cells in (1,1), (1,2), (1,3), (1, 4) ....".
The simple description of it is "oh, we get * in the first horizontal row".
Hence, "sum of 4 vertical columns minus the 3 horizontal rows" is equivalent to "the remaining horizontal row".
Log in to reply
@Calvin Lin – I think I get it. Thank you for taking the time to explain it some more.
i didn't know the values either so i used some websites the these are the values it gave: L=3 O=7 V=1 E=0 if you substituted letters with those numbers, they give the right answers so i guess these are the right values
While I now see that Calvin's solution is far superior to mine, I was able to determine the values of L, O, V & E fairly quickly using this train of thought.
Look at the 2nd row and the 2nd column; they only differ by one letter each. If we let 2O+E=X, then we have the equations X+L=17 and X+E=14. From this we can determine that L=E+3. Now look at the last column. If we replace L with E+3 we get 4E+3=3, meaning that E=0, and therefore L=3.
By replacing L=3 and E=0 we can easily find the other two variables. Looking back at the 2nd row we get 2O=14, meaning that O=7, and finally looking at the 3rd row we get V+3=4, meaning V=1.
We have our variables, so summing them is the easy part:
L + O + V + E = 3 + 7 + 1 + 0 = 1 1
I came up with the question with those initial values, and then placed the numbers randomly on the grid and made sure I could solve it. Didn't think it was as easy as @Calvin Lin 's approach.
This solution helped me a lot..Thanks..!!
I got the same letters by doing:
2L+2O=20 so L+O=10
2O+2E=14 so O+E=7
(L+O)-(O+E)=10-7=3 but the Os cancel each other out and so L-E=3 meaning that L is 3 more than E
L+O+V+E=11 (as we all know by now)
L+2E+V=4
(L+O+V+E)-(L+2E+V)=O-E (because they again cancel all the other letters out) O-E=11-4=7 meaning O is 7 more than E
If O is 7 more than E then we can substitute O+E=7 to 7+0=7 (presuming that all the digits are positive)
So if O=7 then we can substitute L+O=10 for 3+7=10
So if:
L=3
O=7
V=?
E=0
Then V must equal 11-(3+7+0)=1
I did it differently:
From column 2 (O+O+L+E=17) minus column 4 (E+E+E+L=3) we can determine that 2O-2E=17-3=14. Thus, O-E=7.
Row 3 (L+E+V+E) differs from Row 1 (L+O+V+E) by (O-E).
Row 1 = Row 3 + (O-E) = 4 + 7 = 11
Still don't need to know what the actual values of L, O, V or E are.
L = 3
O = 7
V = 1
E = 0
♥️ = (20 - 20) + (17 - 14) + (9 + 3 - 4)
= 0 + 3 + 8
= 11
Do any of us actually know the value of love? I❤I
L=3 , O=7 , V=1 and E=0 so, LOVE=11 :)
I found that realizing that 2O+2L=20, then O+L must equal 10, so keeping that in mind, the second column, O O E L, O+L=10, so O+E must equal 7, then, the third column which equals 9, has V E V O, and O+E=7, which leaves two V's, so 2V=2, so V=1 then, in the fourth column, we have E E E L, which has the sum of three, since V=1, we can eliminate E=1, so, we have to get a sum of three using four numbers, with that in mind, L=3, with E=0 being the only other option, so, we have L=3, V=1, and E=0, to solve for O, we can use the earlier equation, that O+L=10, put in the value of three for L, and we eventually get that O=7, then we input the values to check ourselves, and when everything hecks out, the answer for L O V E is 11
(20+17+9+3)- (14+4+20) =11
Start with 4th horizontal column minus second: 2O + 2L = 20 - 2O + 2E = 14 You get 2L - 2E = 6. Then make a system of equations using 4th vertical column: 2L - 2E = 6 - 2L + 6E = 6 You get -8E = 0. This means E=0 which you can plug in for the rest of the numbers to solve
L is 3, O is 7, V is 1 and E is 0, therefore ♡ = 11
I like this problem, because there isn't a need to find the exact values of L, O, V, E, in order to solve it.
Instead, notice that the sum of the 4 vertical columns, minus of the 3 other horizontal columns, gives you the first horizontal column. In particular,
♡ = ( 2 0 + 1 7 + 9 + 3 ) − ( 1 4 + 4 + 2 0 ) = 1 1 .
Note: I do not know what the values of L, O, V, E are.