How tall?
Ecco, a dolphin, is trying to jump through a circular hole in his enclosure to escape from the aquarium.
From Ecco's perspective just under the water's surface, does the hole seem easier or harder to fit through? And does it seem higher or lower?
Select one or more
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Great Answer!!Please tell me What's the proof of Snell law .
Log in to reply
Hey Tanmay
Snell's law can be easily derived using Fermat's principle of least time as a given (Without this principle, it takes a bit more time, and is outside the scope of this problem). This principle states that light will follow the path from a point source that takes the least time.
The analogy I often hear is that a point source in a low index material is like a lifeguard on a beach, trying to get to a drowning swimmer out on the surf as quickly as possible. But the life guard can run faster than they can swim, so the path they take isn't a straight line (like they would if the person needing help was on the beach.
Just like the lifeguard swimming slower than they can run, light goes slower in a high index material (velocity is n c ). So the time it takes the lifeguard to reach the drowning person is:
T = c / n 1 d 2 + a 2 + c / n 2 b 2 + ( c − d ) 2
Where each term is the distance of the diagonal path (from calculating the hypotenuse) divided by the velocity. To find the minimum of this distance, we can minimize with respect to one of the variables of the path. It doesn't really matter which one we do, but let's minimize with respect to d , the horizontal length of the path in the "fast" medium and set it to zero to find the minimum:
d d d T = c / n 1 d 2 + a 2 d − c / n 2 c − d 2 + b 2 ( c − d ) 2 = 0
Here we need to notice that these two terms are really just ratios of different lengths of the two triangles formed in the diagram above. The first term is the ratio of the length "opposite" to θ 1 to the hypotenuse of the top triangle, and the second term is the ratio of the length "opposite" to θ 2 to the hypotenuse of the bottom triangle. The ratio of opposite:hypotenuse is just the sine trig function:
c n 1 sin θ 1 − c n 2 sin θ 1 = 0
Rearrange this expression, and notice that there's a factor of the speed of light c on both sides yields:
n 1 sin θ 1 = n 2 sin θ 2
So a lifeguard should follow the same path light does, if they want to make it to the drowning person as fast as possible. I encourage you to add this derivation to Brilliant's Wiki on Snell's Law .
I think BOTH answers #1 and #3 are true. So choosing #1 shouldn't be accounted as incorrect :-/
I think there's a flaw in this argument. Specifically, the line
∠ A D B = θ i bottom − θ i top
In your diagram, the triangle ADB follows the red-dashed lines (optical path without water). The incident angle for Snell's Law, however, is the angle the solid green lines make with the water, which is not the same. The relationship depends on a third variable, Ecco's depth below the water. They are nearly the same if Ecco is very close to the surface of the water, but the problem doesn't state that as an assumption.
I believe the hole can appear either larger or smaller, depending on the details of the setup. As an example of a case where it appears larger, consider if the bottom edge of the hole is right at the surface of the water, and Ecco is a significant depth below. The light ray from this bottom edge will enter the water almost immediately, so the apparent optical path will almost exactly coincide with the actual direction (optical path without water); Ecco will agree that the bottom edge is at the water's surface. The top edge, however, will still appear higher. So, the size will appear larger.
Am I missing something, or is the given answer incorrect?
Log in to reply
Hi Robert-
You're right -- I was playing a bit fast and loose with my angle labels in the first "simple" diagram. I've moved up the actually correct diagram that I used to prove the general case. This diagram takes into account the small distance between the two points on the surface where the rays from the top and bottom of the whole arrive. In this case, depth shouldn't matter if I understand your argument correctly. Take a look at the second diagram and let me know.
This sounds like something I should try out with a water-proof camera. For incident angles that are very close to 9 0 ∘ , the angle of refraction should still be less than the angle of incidence and make the hole appear just a bit higher from Ecco's point of view. Based on the shape of the sin function, this difference will be minimized as the hole approaches the water, but should still exist (I think). But if the hole hits the water, you're probably right that total internal reflection would make Ecco agree that the hole is at the water's surface, and the top would be a bit higher.
Let me know if you agree with this, if so I'll suggest we specify that the hole is above the water line.
Thanks for the feedback!
Log in to reply
Thanks for replying! Your edit has indeed fixed my initial objection, but I think there's still a problem later on. Your derivation compares Δ i and Δ r , but I don't think Δ i is the relevant quantity. This is the angle we'd see if we continued the lines A X and B Z to their (unrefracted) intersection, but these lines don't converge at Ecco. The angle that would be subtended by the hole, without refraction, from Ecco's real perspective, is ∠ A D B = θ i bottom − θ i top .
I still think this quantity depends on Ecco's depth, as well as the height of the hole. I whipped up a quick simulation in Mathematica, and it does look like the hole can look either larger or smaller.

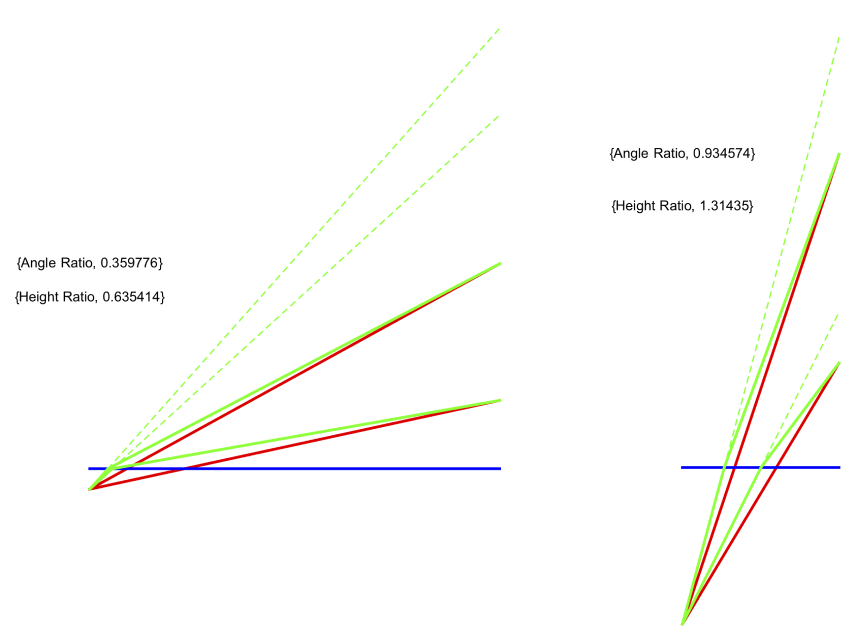
This one has the image larger than the actual hole (the number in the top-left is the ratio).

This one has the image smaller. So unless I made an error in my code, the answer should be that either is possible.
For my part, my intuition about the hole being at the surface was incorrect. I thought the image's position would have to be continuous, or else there would be gaps, but I forgot that for small viewing angles, there would be total internal reflection, so a discontinuity as the hole crosses the surface is natural. I think this is what you were getting at in your second paragraph.
This has been a really interesting problem to think about! The first part, about the hole being higher or lower, could've almost been a "basic" problem, but the size question seems more "advanced".
Log in to reply
@Robert Buckley – Hey Robert-
You inspired me to rig up a Mathematica simulation myself, and tried to find the same kind of conditions that you did.
It looks to me like you projected back the refracted angle to the original distance of the hole, and took the difference of the apparent "top" and "bottom" to determine the hole's apparent size. While in my calculation, I used the subtended angle as a measure of the holes "size" from Ecco's point of view. I totally agree with you though that using the difference of the incident angles does not reflect accurately the subtended angle that Ecco would actually see were the water removed, so I've used the correct angle below. I've shown both ratios in the images:
It's really tough to nail down the exact position of an object's image after being refracted, and I had a tough time convincing myself that projecting the refracted angle back all the way to the actual x-position was the right approach.
Last weekend when I was thinking about this I tried my hand at an experiment (with a sink, suspended ball, and a very wet cell phone) and the ball definitely looked vertically compressed in every photo I took from under the water. So I ended up taking subtended angle as a closer approximation for how our eyes see objects' size.
What are your thoughts on using subtended angle instead of the height measure that (I think) you used. Please correct me if I misinterpreted your approach.
Log in to reply
@Blake Farrow – Yes, you've correctly interpreted my approach. Apologies for not being more clear - I was in a bit of a rush, and I realized shortly afterwards that the difference between angle and image height was probably the source of our disagreement.
The reason I chose to compare image heights rather than angle (besides being marginally easier to code) was that I assumed Ecco was smart enough to know that even if something looks smaller because of distance or viewing angle, it doesn't mean it actually IS smaller. If the humans working at the aquarium realize the security risk the hole poses, and move it farther up above the water (without changing its actual size), Ecco doesn't think it's harder to fit through than before. In other words, I assumed: -Ecco has depth perception, and can see how far away the wall is (and knows it is a vertical plane, in which the hole lies) -Ecco can form a mental model of the setup, and thus determine the actual size of the hole from the angles he sees (and this actual size is what determines how easy it is to fit through) -Ecco does NOT understand refraction, and so forms his mental model as though he was looking through air (or, equivalently, as though the whole setup was underwater). But I can understand how you could interpret the question differently. It's a bit tricky to disentangle the perspective effects from the refraction effects.
Just now I edited my code to include the angle measure, and I can confirm that the angle ratio is less than 1 in all cases. So it seems our math is in agreement now. And it's cool that you've done a practical test too!
Edit: You are right Blake.
TLDR: When projected back to the vertical plane the hole IS bigger but it takes up a smaller proportion of the field of view and therefore on the retina of the dolphin. Counter intuitively, the space between the horizon and the bottom of the hole takes up more of the field of view of the dolphin than it would if she were not under water.
Edit: Thanks Blake for the answer and the tip for posting graphics.
Yes, I agree that the difference in the subtended angles get smaller and you are right about where I was going with it, the projected difference in the height of the hole gets larger.
Lets see if I can post these images (Edit: Got it working. Need to use imgur's direct link)

Let's focus on one of the rays:

Doing some trigonometry:
sin
θ
r
sin
θ
i
=
v
r
v
i
=
n
i
n
r
=
n
θ
r
=
sin
−
1
(
n
sin
θ
i
)
x
=
y
i
tan
(
θ
i
)
y
r
=
y
i
tan
(
θ
r
)
tan
(
θ
i
)
y
r
=
y
i
cos
(
θ
i
)
n
2
−
sin
2
(
θ
i
)
What does this function look like for n=1.33

It's always greater than n.
Here's an example from the dolphins veiwpoint then with n=1.33:

another example from the dolphins veiwpoint then with n=2.0:

So maybe you are right, maybe the angle is more important. But if it is, then won't the hoop appear to be lower, because the angle between the horizon and the centre (or bottom) of the hoop will also be made smaller. Edit: No, strangely, the angle of view taken up by the piece from the bottom of the hoop to the horizon is bigger when viewed from the water. In this example it increases from 15 degrees to 19 degrees.

Well done Blake. I am very impressed that you experimented with your phone, just to make sure.
Log in to reply
Hey Michael-
I think I see where you're going with this, but it's a bit tricky to post graphics in a reply. If you can upload an image (even to Brilliant, in a wiki or another post), you can post it with the link like this:
{: .center}
In your calculation I imagine you're looking at the height of the top and bottom of the hole by projecting the angle of refraction back to the same horizontal distance where the hole actually is. I played around with this a bit in Mathematica and saw something similar: the difference in heights between the top and bottom of the hole are greater after refraction. This confused me a lot because I actually did an experiment (with a sink, suspended ball, and a very wet cell phone) and the ball definitely looked vertically compressed from under the water.
I ended up discarding the analysis that involved trying to calculate the apparent heights y r top and y r bottom in favor of how we actually perceive objects, by the angle they subtend in our vision. Do you agree that the subtended angle of the object (or hole, or whatever) becomes smaller after refraction?
Excellent answer, but the junior school intuition for light into a slower medium of the good ol’ two wheels on an axel going into a sandpit at an angle is all you need to answer the quiz.
Let’s not get into the photon explanation of optics, at uni in my day in junior physics Astronomers used photons and light interchangeably. It is only recently I hear YouTube physicists making the distinction of lightwaves as a classical physics theory where light slows in a medium like glass and water. But in the quantum theory, photons ALWAYS travel at the theoretical lightspeed no matter the medium, at the quantum level between atoms or inside atoms there is no medium, hence
https://youtu.be/mICTVow3-3I
https://youtu.be/CiHN0ZWE5bk
As water has larger refractive index when compared to air so the light rays from the dolphin travel through the water and when they reached the water-air contact surface tue light rays bend away from the normal (since water has more refractive index and light bends away from the normal when it enters into rarer medium from denser medium)
Therefore, from the frame of dolphin the hoop looks smaller in size and higher than it really is.
Note : The options say harder to fit in which is nothing but smaller in size.
Fermat's Principle states that light takes the path between two points that minimizes time. When considering the refraction index of air and water, one must note that light moves faster through air than it does through water. So to minimize time, light travels a longer distance through the air than through the water. Now consider the line between the tip of the dolphin's snout, and the point at which light hits the water based on this least-time principle. This is, in a sense, the dolphin's perception of the hoop, where the slope of the line determines the "height" of the loop from the dolphin's perspective. Now consider the line drawn directly through the tip of the dolphin's snout, and the hoop (imagine the line passing through the center of the hoop). This is, in a sense, the accurate representation of the "height" of the hoop (this is how the dolphin would see the hoop if the water didn't exist). The slope of this line is less than the slope of the line that light actually takes, so the hoop appears higher from the dolphin's perspective.
To determine whether, from the dolphin's perspective, the hoop seems easier to fit through, we will apply Fermat's Principle once again. This time, we consider two paths, each of which represents the path that light would take to hit the dolphin from the hoop. One path runs through the top of the hoop, and the other path runs through the bottom of the hoop. Now we will draw two lines. This time, we connect the top of the loop directly to the tip of the snout, and we do the same with the bottom of the loop. We consider a hoop to appear "harder" to go through if the length of the line segment between the two points at which light hits the water from our paths.. is less than the length of the line segment between the the two points at which those two lines hit the water. Although I am not able to prove this myself, it is true that the hoop appears "harder" with these metrics. To assure myself of this fact, I applied the following heuristic:
Let f(x) be the function whose output is the length of the line segment between the two points at which light hits the water given the paths between the top/bottom of the hoop to the dolphin. The input of this function is x = n.water / n.air, the ratio of the refraction indices of water and air. If we let this ratio grow infinitely large, we see that the path traced by any point on the hoop to the dolphin goes directly from the hoop, to the point on the water directly above the dolphin, then straight down (this is to minimize the distance spent in the water). Because this applies to any point on the hoop, the points at which the paths from the bottom and the top of the hoop to the dolphin hit the water will become infinitesimally close, as those points approach the same value. So for the function f(x), as x approaches infinity, f(x) approaches 0. Now we must make an assumption: The derivative of f(x) is negative for all x < 1. This can be reasoned by letting the ratio of the refraction indices of water and air increase, and imagining what happens to the paths from the top/bottom of the hoop to the dolphin. Note that as this ratio, x, approaches infinity, f(x) approaches 0, which means that if f(x) is well defined (which we assume it is), and if there exists any c such that f(c) > 0, there must be some interval on f(x) for which the derivative of f(x) is negative. I assume the entire interval [1, inf] has the derivative of f(x) be negative because in order for the derivative of f(x) to become positive, there must be some ratio at which the aforementioned line segment starts increasing. In my analysis when solving this problem, I saw no such ratio existing.
Now with all this in mind, the calculus becomes simple. Note that when we drew the lines from the top/bottom of the hoop to the dolphin, we had the scenario where the refraction indices of the water and air are equal: where x = 1. Also note that the length of the line segment connecting the two points at which the lines hit the water is indeed some positive number (this can be evaluated geometrically using the picture). Now we have a c where f(c) > 0, because c = 1 and f(1) > 0. In the problem, we are given a ratio n.water/n.air = 1.33/1 = 1.33. Now we consider the assumption that the derivative of f(x) is negative for all x > 1, and deduce that f(1.33) < f(1). Therefore, The hoop appears harder to fit through from the dolphin's perspective.
So, BOTH #1 and #3 answer are correct. But I got an "Incorrect answer" by choosing #1. This should be fixed, shouldn't it?
Log in to reply
It seems that all replies disregard one very important factor. Ecco sees the circle as a circle and just where it is. The vision of Ecco is not the vision of a human and Ecco is equipped to see things as they are. So from Ecco's perspective none of the options given are correct.
I got confused with quote:The derivative of f(x) is negative for all x < 1;Now we consider the assumption that the derivative of f(x) is negative for all x > 1. It's just my comment saying that it is not an easy way to explain this problem or there is a flout.
Log in to reply
This was a typo on my end, a very evident one at that. It should always read "x > 1". Thanks for pointing it out!
sina/sina'=sinb/sinb'=n(water)
sina'/sinb'=sina/sinb
Δθ(out of water)=b-a
Δθ(in water)=b'-a'
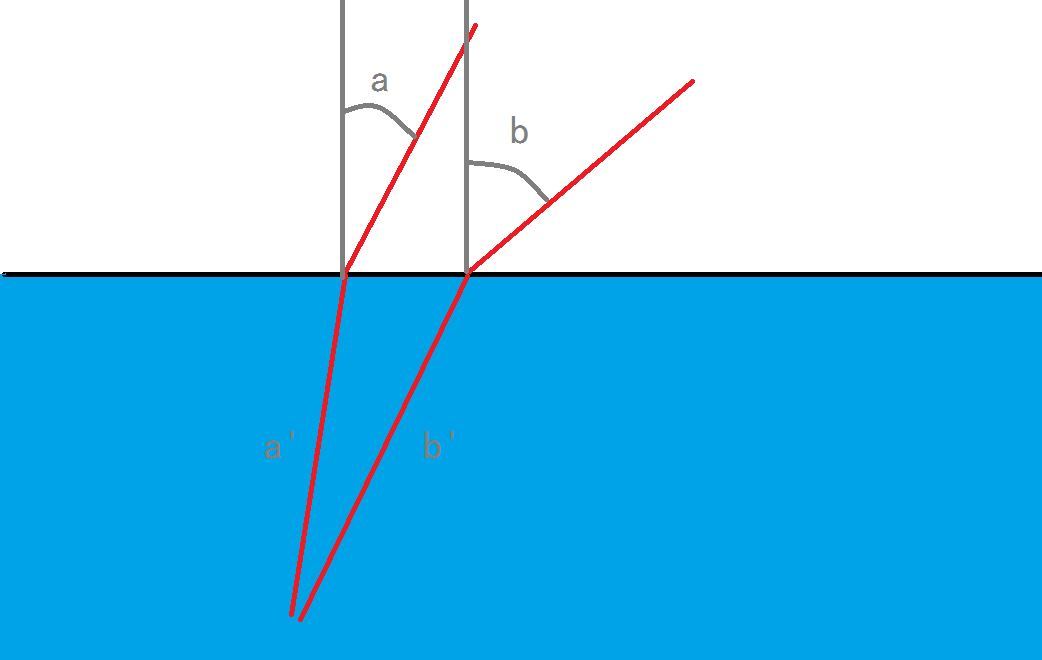 then look at the unit circle:attention that sina'/sinb'=sina/sinb
then look at the unit circle:attention that sina'/sinb'=sina/sinb
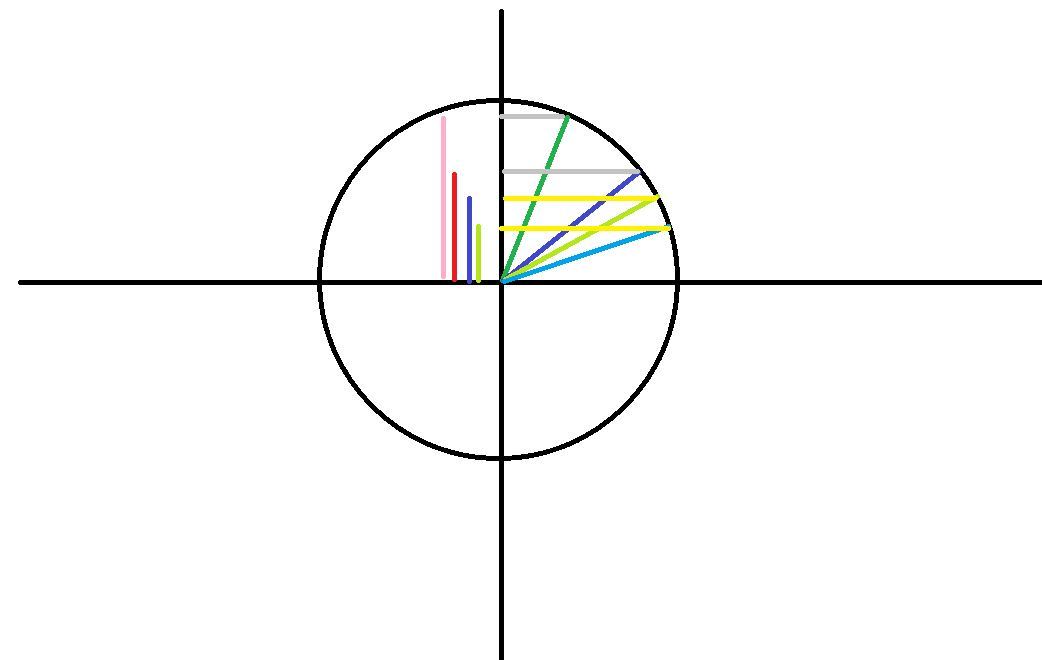 and that is (here I use "L" for "the length of xx color line in the left") Lpink/Lred=Lpurple/Lgreen
so it's apparent that the angle between the green line and the dark blue line in the right (the verticle angle when seeing the lights above water) is bigger than the angle between the light green line and the light blue line in the right (the verticle angle when seeing the lights under water), which means an overwater object's vertical size appears to be smaller when being seen under water
(sorry , I'm having trouble using my mouse, which was making me mad while I was drawing.....)
and that is (here I use "L" for "the length of xx color line in the left") Lpink/Lred=Lpurple/Lgreen
so it's apparent that the angle between the green line and the dark blue line in the right (the verticle angle when seeing the lights above water) is bigger than the angle between the light green line and the light blue line in the right (the verticle angle when seeing the lights under water), which means an overwater object's vertical size appears to be smaller when being seen under water
(sorry , I'm having trouble using my mouse, which was making me mad while I was drawing.....)
Quick answer:
This is the opposite case of a pencil in a glass full of water where you see the pencil look closer and larger.

Hence, you would expect the object to look smaller and further away.
Well exactly! No need to go into all these Snell’s Law complications, anyone who has ever got into water (i.e. everyone) knows that things appear closer and larger, so obviously the opposite would be the case for the poor dolphin. (What karma are we bringing on ourselves confining dolphins anyway?!)
Ecco's escape
To answer this question, we need to break it down into two pieces:
To tackle both problems, we'll use the diagram below. The rays were drawn following Snell's Law , which governs the angle of incidence and refraction of a light ray passing from one medium with index of refraction n 1 to another with index n 2 . Note that the angles θ are with respect to the normal to the interface.
n 1 sin θ i n 2 n 1 sin θ i = n 2 sin θ r = sin θ r
Check out my reply below for a derivation of Snell's Law.
Since the light rays from the hole to freedom are in air, and Ecco is in water, n 1 = n air = 1 . 0 0 and n 2 = n water = 1 . 3 3 . This means that sin θ r is less than sin θ i . Since the sine function only increases from 0 to 9 0 ∘ , this implies θ r must be less than θ i : The angle of refraction is less than the angle of incidence, and so the ray will bend towards the normal going from air to water.
Should Ecco aim high or low?
The apparent image of the hole as it appears to Ecco is found by extending the refracted beam back to the wall. Since the angle of refraction is less than the angle of incidence, this image appears to be coming from higher in the sky than the actual hole. Ecco will have to aim low for his jump.
Does it look like Ecco can fit?
To figure out how large the hole looks from Ecco's perspective, we'll need to look at two points on the hole. One at the top A and one at the bottom B . The corresponding points on the apparent image of the hole are A ′ and B ′ . We'll use the angle subtended by the hole in Ecco's vision as a representation of its apparent "size". So the actual size of the hole is Δ i = ∠ Y Z B − ∠ W X A (assuming that Ecco is close to the water's surface) while the apparent size is Δ r = ∠ Y Z B ′ − ∠ W X A ′ . This angle is just the difference of the angle coming from the bottom of the hole, to the one coming from the top of the hole. For the real size, it's the incident angles, and for the apparent size it's the refracted angles:
Δ i = θ i bottom − θ i top Δ r = θ r bottom − θ r top
To keep things simple, let's just say that the real hole subtends an angle of 3 0 ∘ , with the incident angle from the top measuring 3 0 ∘ from the normal, and the incident angle from the bottom measuring 6 0 ∘ from the normal. We can calculate their angles of refraction using the equation we used above:
sin θ r = n 2 n 1 sin θ i
Using the inverse sine, this yields θ r top = 2 2 ∘ and θ r bottom = 4 0 . 5 ∘ . Since the apparent subtended angle is just their difference, this means from the point of view of Ecco, the hole subtends only 1 8 . 5 ∘ . Thus, it looks smaller, and harder to fit through than it really is.
In general
Above we just picked two random incident angles for the top and bottom of the hole. In the case we looked at, the apparent subtended angle was less than the real one. Is this always true? Let's keep things in general and find out.
The subtended angle of the actual hole is just:
Δ i = θ i bottom − θ i top
And the apparent subtended angle of the hole's image is:
Δ r = θ r bottom − θ r top
Using the first equation we derived from Snell's law, and the inverse sine, we can substitute in that expression for the angles of refraction:
δ r = arcsin ( n 2 n 1 sin θ i bottom ) − arcsin ( n 2 n 1 sin θ i top )
There might be some way to simplify this and express it in terms of θ i bottom − θ i top , but nobody's got time for that. Let's just plot it for all θ i bottom > θ i top (orange) and compare it to the real hole's subtended angle (black):
The image's subtended angle (and size) is less than the real hole's for all incident angles (so for all positions of the hole).