How To Construct a 4D Menger Sponge
The Problem

The volume of a modified 4D Menger Sponge, which is created by successively subtracting volumes from the interior of a 4D tesseract of side length of 2, can be expressed as
where and are positive integers with coprime.
Find the sum .
The method of successively subtracting volumes from the interior shall now be explained
Preliminaries
Given an arbitrary odd number , we have the set of digits in base . Then we construct all possible distinct sets of the form
where are digits from that first set, and need not be different, i.e., may be the same as . Then for each such distinct set, we list all possible distinct permutations of it. For example , let the odd number be , where , and we have the set of digits . We then will have the following distinct sets
and then for example, for the set , we have the following permutations
Thus, we will have a total of such sets with this example
Subtraction of Volumes
Given a tesseract, for example , we can subdivide it into smaller tesseracts, of which the 4D coordinates of each can be described as . We subtract the 113 smaller tesseracts as per the list of 4D coordinates. If we sort the list by the first tuple, that is
where are arbitrary digits, then the "layers" will look like this, the green blocks being subtracted

while "layer" will look like this, the green blocks being subtracted
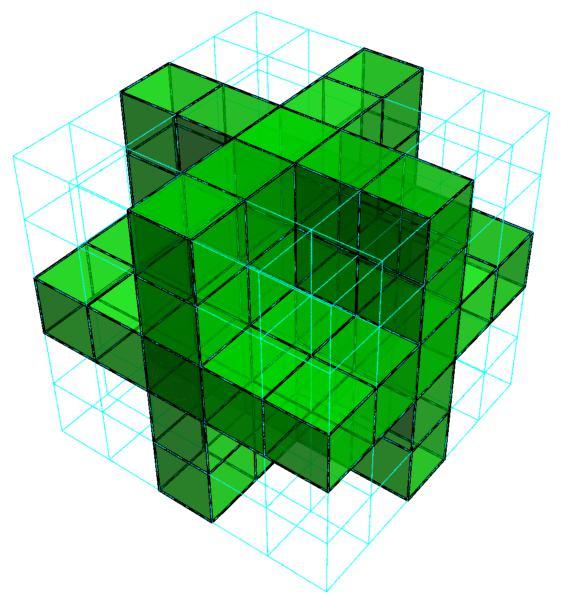
Because there's already so many occurrences of the digit , it shouldn't be hard to see that the "middle layer" of is going to have a lot of green blocks being subtracted from it.
Even though these graphics look like 3D graphics, they are still a valid projection of 4D tesseracts, we can imagine each green block as a tesseract each with its own coordinates.
Method of Successive Subtractions
The classic 3D Menger Sponge is created from a 3D cube by letting for all recursive steps, and the sets are of the form
where , always. After the first round, of the volume of a 3D cube is subtracted. Then for the 2nd round, EACH of the remaining cubes has of their volumes removed. Repeat for the 3rd round and thereafter. We can see that starting with an intial volume of we are reducing it by a factor of successively. Since the infinite product of this fixed fraction has the limit of , the classic 3D Menger Sponge has a volume of as the limit. We are going to do things slightly differently here.
Here, instead of letting for all recursive steps, the value is going to be where stands for the th recursive step. That is, in the case of the modified 4D Menger Sponge, which has the volume , the first round will reduce it by a factor of
.
The 2nd round will reduce it by a factor of
And so on. The infinite product has a limit value which is not zero. What is the final volume?
Note
Here's how a 3D Menger Sponge looks like, after a few recursions, to help with visualizing this problem. Try to generalize from 3D to 4D. This one, as already noted, will have zero volume.

The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The volume is 2 1 π 2
which is the volume of the 4-Sphere of radius 1 , so that the answer is 1 + 2 + 2 = 5 . In fact, carrying out the same recursive subtractions from n-Cubes of sides 2 will yield the correct volumes of corresponding n-Spheres of radius 1 , as in
1D 2
2D π
3D 3 4 π
4D 2 1 π 2
5D 1 5 8 π 2
6D 6 1 π 3
7D 1 0 5 1 6 π 3
8D 2 4 1 π 4
9D 9 4 5 3 2 π 4
etc.
For the 4D case, we first find the number of permutations of the set of numbers ( n , n , a , b ) . There are 4 cases to consider, which are
( n , n , n , n )
( n , n , n , a )
( n , n , a , a )
( n , n , a , b )
where a = 0 , 1 , 2 , … . 2 n EXCEPT n
Then the number of possible permutations of each are, respectively
1
4 ⋅ 2 n
1 ⋅ 2 4 ⋅ 3 ⋅ 2 n
4 ⋅ 3 ⋅ 2 1 2 n ( 2 n − 1 )
Subtracting all of this from ( 2 n + 1 ) 4 , we end up with
1 6 n 3 ( n + 2 )
so that the infinite product we seek, giving the limit volume, is
2 4 n = 1 ∏ ∞ ( 2 n + 1 ) 4 1 6 n 3 ( n + 2 )
which can be rearranged as
2 4 n = 1 ∏ ∞ ( 2 n + 1 ) 4 ( 2 n ) 2 ( 4 n 2 + 8 n )
Given the infinite product
n = 1 ∏ ∞ n ( n + 2 ) ( n + 1 ) 2 = 2 1
we then can modify the previous infinite product to as follows
2 3 n = 1 ∏ ∞ ( 2 n + 1 ) 4 ( 2 n ) 2 ( 2 n + 2 ) 2
But given another well-known infinite product, the Wallis product
n = 1 ∏ ∞ ( 2 n + 1 ) 2 ( 2 n ) ( 2 n + 2 ) = 4 π
we have the following volume as the limit
2 3 4 2 π 2 = 2 1 π 2
Note: The following infinite product will deliver the volume of the n -Sphere of radius R
( 2 R ) n k = 1 ∏ ∞ ( 2 k + 1 ) n ( 2 k ) n − 1 ( 2 k + n )
which can be derived from the same method of subtracting volumes from n -Cubes, creating modified n -Menger Sponges. For n = 2 , the infinite product becomes the Wallis product.