How to perfect the bottle flip?
A lot of skill goes into whether you can achieve a bottle flip. But with a bit of physics, you can maximize your chances by optimizing the volume of water in the bottle. Over- or under-filling the water bottle yields a high center of gravity, which can cause the bottle to tip over on landing, even if the throw is otherwise perfect. To stabilize the bottle's landing, the center of gravity should be as low as possible.
Treat an empty water bottle as a cylinder with mass 1 2 g evenly distributed along its length. What is the water level h in centimeters such that the bottle's center of gravity is lowest?
Note: The density of water is about 1 g / c m 3 .

The answer is 2.270083225.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Hi, I wonder why h1 for the bottle is 20 cm, the top of the bottle, and not 10 cm, the middle of the bottle.
Thanks.
Log in to reply
Thanks for pointing out. Amended!
It is 10 cm, it's written 20/2.
I agree with Ivo, the centre of mass of the bottle should be 10 cm not 20 cm. The solution by Binky Mh does this and finds the centre of mass of the bottle+water to be (3h^2+20)/(6h+2) which is half of value of Donglin Loo ((3h^2+20)/(3h+1)).
Log in to reply
Oops. That was my mistake. Thanks for pointing out. Amended!
How didi you get the height of the bottle 20 cm....? 36 is what ??
Log in to reply
@Bikram Sharma The 3 6 ( c m 2 ) refers to the area of the base of the cylindrical bottle. The 20cm refers to the height of bottle. It should be half because we are locating the center of mass of bottle.
Log in to reply
A lot of skill goes into whether you can achieve a bottle flip. But with a bit of physics, you can maximize your chances by optimizing the volume of water in the bottle. Over- or under-filling the water bottle yields a high center of gravity, which can cause the bottle to tip over on landing, even if the throw is otherwise perfect. To stabilize the bottle's landing, the center of gravity should be as low as possible.
Treat an empty water bottle as a cylinder with mass evenly distributed along its length. What is the water level in centimeters such that the bottle's center of gravity is lowest?
Note: The density of water is about
Log in to reply
@Bikram Sharma – What I mean is when substituting the values h 1 , h 2 , h 1 = 2 2 0 , h 2 = 2 h . h 1 , h 2 refer to the center of mass of the bottle and water respectively and separately(not together!). Hope it helps
Bikram, these values are from the image, they're not explicitly stated in the problem text...
To find the total centre of gravity
C
t
, we can take the centre of gravity of just the water
C
w
, the centre of gravity of just the bottle
C
b
, and find the point where the distance from each centre is the ratio between the mass of the bottle
M
b
and the mass of the water
M
w
.
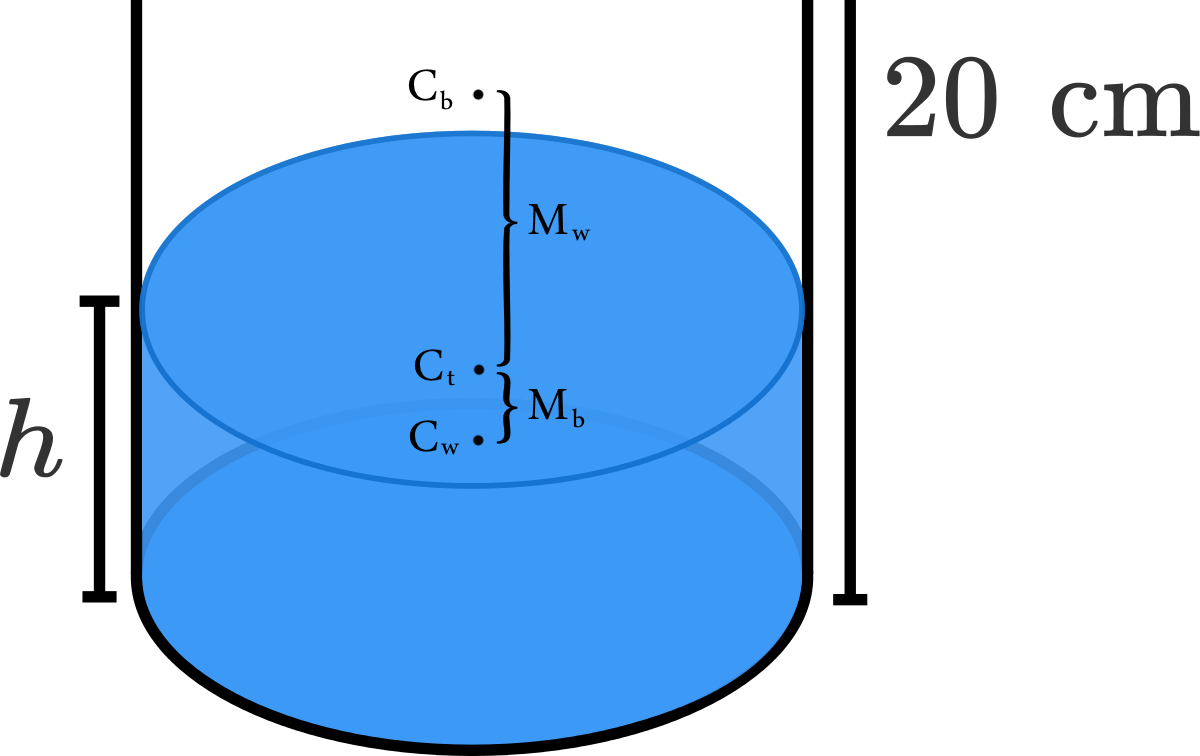 To do this, we find the distance between the two centres
C
b
−
C
w
, divide this by
M
w
+
M
b
, and then multiply it by
M
b
. We can then add this to
C
w
to find
C
t
.
C
t
=
C
w
+
(
C
b
−
C
w
)
×
M
b
+
M
w
M
b
We can now substitute the information we're given in the question to get:
C
t
=
2
h
+
(
1
0
−
2
h
)
×
1
2
+
3
6
×
h
1
2
Simplify:
C
t
=
2
h
+
(
1
0
−
2
h
)
×
1
2
+
3
6
×
h
1
2
=
2
h
+
2
+
6
h
2
0
−
h
=
6
h
+
2
3
h
2
+
2
0
To find the local minimum, We need to differentiate this, using the quotient rule:
d
h
d
(
6
h
+
2
3
h
2
+
2
0
)
=
(
6
h
+
2
)
2
(
6
h
+
2
)
(
6
h
)
−
(
3
h
2
+
2
0
)
(
6
)
=
2
(
3
h
+
1
)
2
3
(
3
h
2
+
2
h
−
2
0
)
We then set it to equal
0
in order to find the local minimum, which we then solve:
2
(
3
h
+
1
)
2
3
(
3
h
2
+
2
h
−
2
0
)
=
0
Divide both sides by
2
(
3
h
+
1
)
2
3
:
3
h
2
+
2
h
−
2
0
=
0
Divide both sides by
3
again, then add
3
2
0
:
h
2
+
3
2
h
=
3
2
0
Then add
9
1
so the left side of the question can be expressed as a square:
h
2
+
3
2
h
+
9
1
=
9
6
1
(
h
+
3
1
)
2
=
9
6
1
And now we can easily solve for
h
:
h
+
3
1
=
3
6
1
h
=
3
6
1
−
3
1
≈
2
.
2
7
0
1
To do this, we find the distance between the two centres
C
b
−
C
w
, divide this by
M
w
+
M
b
, and then multiply it by
M
b
. We can then add this to
C
w
to find
C
t
.
C
t
=
C
w
+
(
C
b
−
C
w
)
×
M
b
+
M
w
M
b
We can now substitute the information we're given in the question to get:
C
t
=
2
h
+
(
1
0
−
2
h
)
×
1
2
+
3
6
×
h
1
2
Simplify:
C
t
=
2
h
+
(
1
0
−
2
h
)
×
1
2
+
3
6
×
h
1
2
=
2
h
+
2
+
6
h
2
0
−
h
=
6
h
+
2
3
h
2
+
2
0
To find the local minimum, We need to differentiate this, using the quotient rule:
d
h
d
(
6
h
+
2
3
h
2
+
2
0
)
=
(
6
h
+
2
)
2
(
6
h
+
2
)
(
6
h
)
−
(
3
h
2
+
2
0
)
(
6
)
=
2
(
3
h
+
1
)
2
3
(
3
h
2
+
2
h
−
2
0
)
We then set it to equal
0
in order to find the local minimum, which we then solve:
2
(
3
h
+
1
)
2
3
(
3
h
2
+
2
h
−
2
0
)
=
0
Divide both sides by
2
(
3
h
+
1
)
2
3
:
3
h
2
+
2
h
−
2
0
=
0
Divide both sides by
3
again, then add
3
2
0
:
h
2
+
3
2
h
=
3
2
0
Then add
9
1
so the left side of the question can be expressed as a square:
h
2
+
3
2
h
+
9
1
=
9
6
1
(
h
+
3
1
)
2
=
9
6
1
And now we can easily solve for
h
:
h
+
3
1
=
3
6
1
h
=
3
6
1
−
3
1
≈
2
.
2
7
0
1
Excellent solution, even somewhat intuitively solved!
Log in to reply
Thanks! In all honesty, I wasn't sure if my method was going to work until I put the answer in.
Excellently done indeed!
This is not a solution, the others are fine, but puzzlement that the jar, like Bottom's Dream, "hath no bottom" (MSND, Act IV, end of scene i). If we assume that it hath a bottom, of density equal to that of the sides, then the optimal depth is slightly lower: 2.221487551 cm. However if the base has the same mass as the sides, then the optimal depth is 2 cm exactly.
In this same interlude it doth befall that I, one Snout by name, portray a wall. And such a wall as you may think as had ... a top as well as a Bottom. If you assume the top of the bottle weighs the same as the bottom, and both are included in the overall mass then the centre of mass shifts back to the original answer.
NO CALCULUS: If we imagine the process of adding water into the bottle, we realize that the center of mass will drop as water is initially added and then rise as more water is added above the center of mass. The problem then becomes finding the "turning point". Logically, this point happens when the center of mass is equal to the water line because additional water brings the center of mass up. To calculate the center of mass, we can simplify the bottle to a point mass of 1 2 g in the center of the bottle. Similarly, the water can be represented as a point mass. Let h represent the height of filled water. The mass of water is then 3 6 h and the point is at a height of 2 h . To find the weighted average of the points (the center of mass), we write 3 6 h + 1 2 1 0 ⋅ 1 2 + 3 6 h ⋅ 2 h . The denominator represents the total mass. Since we are finding the point the center of mass is equal to the water line, we can set this equal to h . Multiplying out, we get 3 6 h 2 + 1 2 h = 1 8 h 2 + 1 2 0 , 1 8 h 2 + 1 2 h − 1 2 0 = 0 , 3 h 2 + 2 h − 1 0 = 0 , which yields the solution h = 3 6 1 − 1 = 2 . 2 7 0 0 8 3 2 2 5
well thats clever
I solved this using Solver feature found in most spreadsheet programs. (Libreoffice in my case)
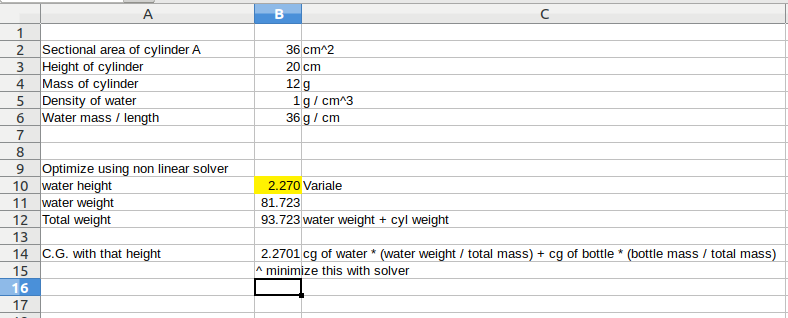
how was it solve?
 先把重心关于h的函数表示出来,然后求导,导数为0时的x值即为重心最小时的h值。
先把重心关于h的函数表示出来,然后求导,导数为0时的x值即为重心最小时的h值。
If added water's height h exaclly equal to height of mass center, it should have lowest center of mass. So we can make this equations: 1 2 + 3 6 h 2 2 0 ( 1 2 ) + 1 ( 3 6 h ( 2 h ) ) = h , simplification get 2 + 6 h 2 0 + 3 h 2 = h . then, 2 0 + 3 h 2 = 2 h + 6 h 2 , − 3 h 2 − 2 h + 2 0 = 0 . use quadratic formula we get h = 2 ( 3 ) 2 ± 4 − 4 ( − 3 ) ( 2 0 ) . simplification get h = 3 1 + ± 6 1 . we don't need negative value, so final answer is h = 3 1 + 6 1 ≈ 2 . 2 7 0 .
First, let's consider the center of mass of the bottle and water separately. Since the mass is evenly distributed throughout the length, the center of mass of the cylinder is at its mid-height. The center of mass of the water is also at its mid-height since the density of water is uniform throughout. Now, since the center of mass are directly on top of each other vertically, we will only consider the vertical component. The center of mass is essentially the weighted average of each center of mass, weighted with the mass at its location. Thus, the center of mass with a given water height of h would be P = 3 6 h + 1 2 2 h ⋅ 3 6 h + 1 0 ⋅ 1 2 = 6 h + 2 3 h 2 + 2 0 P ′ = ( 6 h + 2 ) 2 3 6 h 2 + 1 2 h − 1 8 h 2 − 1 2 0 = 0 1 8 h 2 + 1 2 h − 1 2 0 = 0 ⟹ h ≈ 2 . 2 7
We make use of the formula
h ˉ = ∑ k = 1 n m k ∑ k = 1 n m k h k
Here,
h ˉ = m 1 + m 2 m 1 h 1 + m 2 h 2
Let the water level be h
h ˉ = 1 2 + 3 6 h 1 2 ⋅ 2 2 0 + 1 ⋅ 3 6 ⋅ h ⋅ 2 h = 1 2 + 3 6 h 1 2 0 + 1 8 h 2 = 2 + 6 h 2 0 + 3 h 2
To make ourselves adapt to the problem-solving here better, we can let h ˉ = y , h = x
Our function becomes y = 2 + 6 x 2 0 + 3 x 2
Now, we are trying to find the value of x when y is minimum. You can use calculus(differentiation) to find it but I personally think algebra will do the trick here.
⇒ y ( 2 + 6 x ) = 2 0 + 3 x 2
3 x 2 + ( − 6 y ) x + 2 0 − 2 y = 0
We know that value of x is real.
∴ ( − 6 y ) 2 − 4 ( 3 ) ( 2 0 − 2 y ) ≥ 0
3 6 y 2 − 1 2 ( 2 0 − 2 y ) ≥ 0
3 y 2 − ( 2 0 − 2 y ) ≥ 0
3 y 2 + 2 y − 2 0 ≥ 0
When 3 y 2 + 2 y − 2 0 = 0
y = 6 − 2 ± 4 + 4 ( 3 ) ( 2 0 )
We neglect the negative value of y
We have y ≥ 6 − 2 + 2 4 4
Minimum value of y = 6 − 2 + 2 4 4
x = 6 6 y + 0 = y ≈ 2 . 2 7 0
Water level sought after = h = x ≈ 2 . 2 7 0 c m