How will you solve it?
In a square A B C D , point P is in the square, such that △ C D P is an equilateral triangle. What is the value of ∠ C P B ?
This problem is not original.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Nice solution SIr! Thanks for sharing!
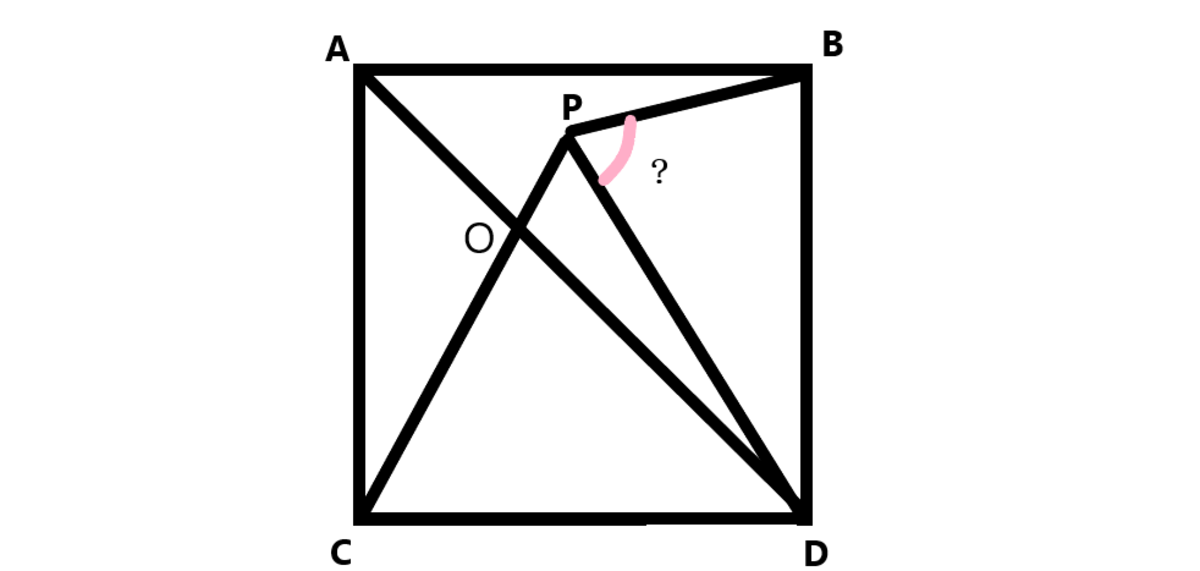 Here's the solution
Here's the solution
I n s q u a r e A B C D a n d E q u i l a t e r a l t r i a n g l e P C D .
Details
AC=CD=PD=BD
ANGLE(ACD)=45 DEGREE ANGLE(PDO)=15 DEGREE
FROM DETAIL 1 PB=BD SO ANGLE(P)=ANGLE(B) P=B=X
NOW we have get all informations IT'S time for solving
In triangle DBP WE say :2X+30=180
WE get our answer as *75 * degree
@Vinayak Srivastava . LOL postednow.. have a look
I think the diagram swaps C and D, it should be the other way around
Please share some other method if you solved it differently, this method is very long.
Log in to reply
bro your method is very long . I've done with the most simple method
Log in to reply
Yes, that is why I posted this, I wished for a simpler method. Please share it!
Log in to reply
@Vinayak Srivastava – yay, WAIT a minute I'm talking to sir
Log in to reply
@Srijan Singh – 52 minutes...
Log in to reply
@Vinayak Srivastava – bruh editing
Log in to reply
@Srijan Singh – give me only 15 minutes
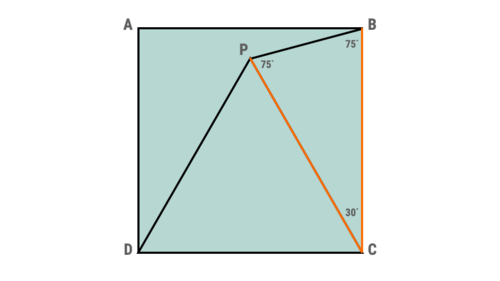
P C = B C ⟹ ∠ C P B = 7 5 ∘
Thanks for sharing your approach! I feel that mine was too much of overkill.
Log in to reply
It is the same explanation as @Chris Lewis gave. Your method is quite good as well, but we should try to seek shorter and brilliant ways to find a solution
Log in to reply
Yes, that is why I posted this easy level 1 problem, I knew there had to be a brilliant solution, but I couldn't find it, and I had to even use trig and search atan(2-sqrt3)! Thanks for making me remember isosceles triangles exist.
Since Δ C D P is equilateral and A B C D is square, P C = C B . So Δ P C B is isosceles.
Also, ∠ P C B = 3 0 ∘ ; so ∠ C P B = 7 5 ∘ .