Hyperbola halving a square
Consider the square enclosed by the lines x = 0 , x = 1 , y = 0 and y = 1 .
The hyperbola x y = a divides this square into two regions of equal areas.
Calculate a .
The answer is 0.18668.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
There's a missing a on the second integral and 1 ln ( 1 ) should be a ln ( 1 )
Log in to reply
Thanks. Will fix it.
Log in to reply
Ain't fixed yet?
Log in to reply
@A Former Brilliant Member – 'Twas fixed only in part. Now it's fixed in its entirety. Thanks y'all for paying such good attention.
@Arjen Vreugdenhil Would it be possible to solve for a analytically? If it is not possible, could you prove it?
Log in to reply
I know it is not possible, but proving it is something I won't endeavor here... :)
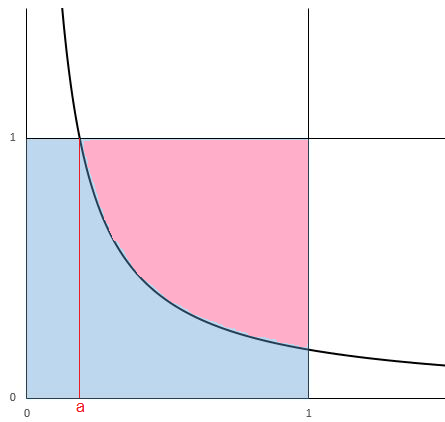 We note that the pink region has an area of
2
1
, and it is given by:
We note that the pink region has an area of
2
1
, and it is given by:
∫ a 1 ( 1 − x a ) d x x − a ln x ∣ ∣ ∣ ∣ a 1 1 − a + a ln a a ln a − a + 2 1 ⟹ a = 2 1 = 2 1 = 2 1 = 0 ≈ 0 . 1 8 7 By numerical method
Good approach.
When I posted my solution, I hesitated between using the blue or the pink region. The blue region requires two separate integrals; the pink region produces two terms under a single integral.
Log in to reply
Thanks for your comments. I noticed that using only a region (pink) to explain is more straightforward and clearer.
We can create a simple rectangle where x 1 crosses y = 1 , ( a , 1 ), with area a ∗ 1 = a , and find the remaining area via integration.
A = a + a ∫ a 1 x 1 d x = a + a l n ∣ x ∣ a 1 = a + a ( l n ∣ 1 ∣ − l n ∣ a ∣ ) = a ( 1 − l n ∣ a ∣ )
The total area of the square is 1, meaning the equally divided segments must have area 2 1 .
a ( 1 − l n ∣ a ∣ ) = 2 1
I solved numerically to get a ≈ 0 . 1 8 7 .
I got the final equation that was (e/a)^a=e^0.5.But I was unable to solve it. Please tell its solution.
Each region has an area of .5. Additionally, we can see that the intersection of the graph and the upper side of the rectangle must be 1=a/x and so x=a. Given this, our area must be the integral from a to 1 added to a. (a*1=a) The integral is alnx so our equation is a + aln(1) - aln(a) = .5... aln(1) = 0 so we can graph y=x and y=aln(a) + .5 for our answer: ~.187
Each of the regions must have area 2 1 . Consider the bottom-left region. We find the area by integration: A = ∫ 0 a 1 d x + ∫ a 1 x a d x = [ x ] 0 a + [ a ln x ] a 1 = a − 0 + a ln 1 − a ln a = a − a ln a . Set A = 2 1 and solve numerically: a − a ln a = 2 1 . The solution is a ≈ 0 . 1 8 6 6 8 .