"I am back" says Integration
∫ e 4 x − e 2 x + 1 e 3 x + e x d x
If the value of the indefinite integral above can be written as arctan ( a e b x − g e d x ) + C , where a , b , d and g are constant integers, find 1 0 1 ( a 2 + b + d 3 + g 4 ) .
Clarification : C denotes the arbitrary constant of integration .
The answer is 202.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Log in to reply
To learn it utilizing time.
Log in to reply
Log in to reply
@Rajdeep Dhingra – This looked very interesting to me. Thanks very much!
Log in to reply
@Lu Chee Ket – Your Welcome. :)
@Lu Chee Ket – See the image below.
 Imgur
Imgur
 Imgur
Enclose Latex code in
R
o
u
n
d
b
r
a
c
k
e
t
s
to display in the same line or in
S
q
u
a
r
e
B
r
a
c
k
e
t
s
to display in other line.
Imgur
Enclose Latex code in
R
o
u
n
d
b
r
a
c
k
e
t
s
to display in the same line or in
S
q
u
a
r
e
B
r
a
c
k
e
t
s
to display in other line.
Hover to see the latex code
Log in to reply
@Rajdeep Dhingra – Please give comment on my very first paste.
Nicely done .
But i told you how to view latex without pasting images.
hover to see Latex codes.If want in continuation in the same line then like
∫
0
3
x
3
d
x
is fine. Or in different line use
∫
0
3
x
3
d
x
 Imgur
Imgur
Log in to reply
Your gradual guiding way looked good to me. I started to feel not that difficult to learn. Starting with some being known, I think we can learn all eventually. Thanks!
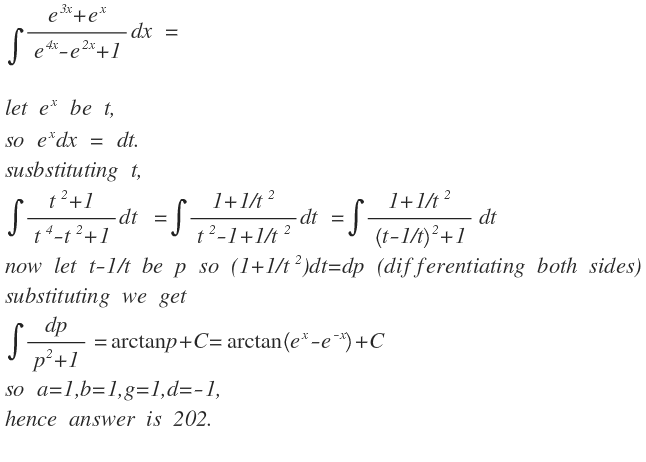

Divide numerator and denominator by e 2 x to write it as: ∫ ( e x − e − x ) 2 + 1 e 2 x − 1 + e 2 x ( e x + e − x ) d x
Substitute e x − e − x = t such that ( e x + e − x ) d x = d t .
∫ t 2 + 1 d t = tan − 1 t + C
= tan − 1 ( e x − e − x ) + C
⟹ a = b = g = 1 , d = − 1
∴ 1 0 1 ( a 2 + b + d 3 + g 4 ) = 2 0 2