This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
There are 2 solutions: -4 & 6.
x^2 - 19 = 2x + 5 x^2 - 2x - 24 = 0 (x - 6)(x + 4) = 0 Then, x = -4, 6
Log in to reply
You have to double check that when you maniuplate an expression, that the final solution set satisfies the original equation.
x = -4 is also an answer in complex number realm.
could u please help, how do you type the the solution, i tried with MS word ,but it looks horrible
Log in to reply
O.K. Use Latex.How to use it ?See this .
Log in to reply
thank u very much, will come back sure with Latex.
Log in to reply
@Manish Kumar Singh – Yeah!!I'll be surely waiting for you:P
Please make the options better. 6 is the only number which lies in the domain of the given function
how can you did it?
why neglect -4? @Calvin Lin
Log in to reply
That's complex logarithm.
In principal logarithm, lo g a x , x > 0 , a > 0 , a = 1
lo g 2 x + 5 ( x 2 − 1 9 ) = 1
Let 2 x + 5 = b , x 2 − 1 9 = x , 1 = y
When lo g b x = y , b y = x
∴ ( 2 x + 5 ) 1 = x 2 − 1 9
∴ 2 x + 2 4 = x 2
∴ − x 2 + 2 x + 2 4 = 0
∴ − x 2 − 4 x + 6 x + 2 4 = 0
∴ − x ( x + 4 ) + 6 ( x + 4 ) = 0
∴ ( − x + 6 ) ( x + 4 ) = 0
Hence, x=6 or x=-4
Substituting x=6 into the logarithm,
lo g 2 ( 6 ) + 5 ( 6 2 − 1 9 ) = lo g 1 7 ( 1 7 ) = 1
Hence , x=6 (Proven)
Log -3/ Log -3 = 1 for x = -4 is also an answer in complex number realm as (-3)^1 = (-3).
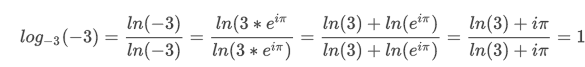
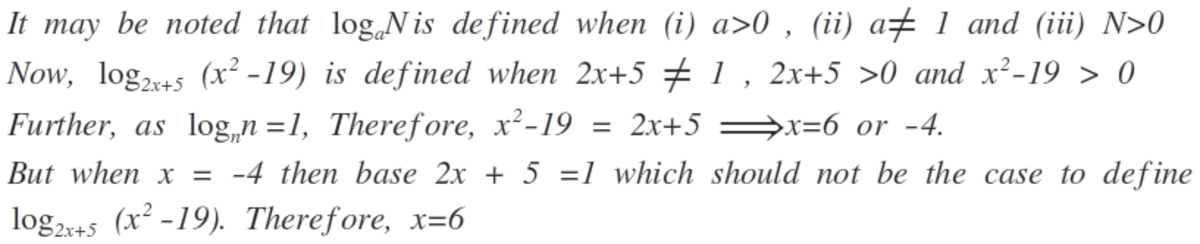
we have lo g 2 x + 5 ( x 2 − 1 9 ) = 1 .Now we know that if lo g x y = z ,then x z = y .we use this in our problem to get: 2 x + 5 = x 2 − 1 9 ⟹ x 2 − 2 x − 2 4 = 0 ⟹ x 2 − 6 x + 4 x − 2 4 = 0 ⟹ ( x − 6 ) ( x + 4 ) = 0 ⟹ x = 6 , − 4 . but lo g 2 x + 5 ( x 2 − 1 9 ) is undefined for negative value of x . ∴ x = 6