I don't know the answer. Do you?

Calculus Level 2

d d x [ arcsin ⁡ ( 2 x 1 + x 2 ) ] x = 1 = ? \large \dfrac{d}{dx} \Bigg[\arcsin \left( \dfrac{2x}{1+x^2} \right) \Bigg]_{x=1} = \ ?

5 1 7 None of these choices 3

View wiki
Surya Prakash by Surya Prakash , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Kishore S. Shenoy
Oct 15, 2015

Let's take the expression right away, without making any confusion. We here use, f ( x ) = sin ⁡ − 1 ( 2 x 1 + x 2 ) = { − π − 2 tan ⁡ − 1 x x < − 1 2 tan ⁡ − 1 x x ∈ [ − 1 , 1 ] π − 2 tan ⁡ − 1 x x > 1 f(x)=\sin^{-1}\left(\dfrac{2x}{1+x^2}\right) = \begin{cases}-\pi-2\tan^{-1}x&x<-1\\ 2\tan^{-1}x&x\in[-1,1]\\\pi-2\tan^{-1}x&x>1\end{cases}

To say that the limit exists, f ′ ( a ) = lim ⁡ x → a − f ( x ) − f ( a ) x − a = lim ⁡ x → a f ( x ) − f ( a ) x − a = lim ⁡ x → a + f ( x ) − f ( a ) x − a f'(a)=\lim_{x\to a^-}\dfrac{f(x)-f(a)}{x-a}=\lim_{x\to a}\dfrac{f(x)-f(a)}{x-a}=\lim_{x\to a^+}\dfrac{f(x)-f(a)}{x-a}

Now let's take left hand and right hand limits. lim ⁡ x → 1 + f ( x ) − f ( 1 ) x − 1 = lim ⁡ h → 0 + f ( 1 + h ) − f ( 1 ) h = lim ⁡ h → 0 + π − 2 tan ⁡ − 1 ( 1 + h ) − 2 tan ⁡ − 1 ( 1 ) h Using L’H o ˆ pital’s rule = lim ⁡ h → 0 + − 2 ( 1 + h ) 2 + 1 = − 1 lim ⁡ x → 1 − f ( x ) − f ( 1 ) x − 1 = lim ⁡ h → 0 − f ( 1 − h ) − f ( 1 ) − h = lim ⁡ h → 0 − 2 tan ⁡ − 1 ( 1 − h ) − 2 tan ⁡ − 1 ( 1 ) − h Using L’H o ˆ pital’s rule = lim ⁡ h → 0 − − 2 − 1 ⋅ [ ( 1 − h ) 2 + 1 ] = 1 ⇒ lim ⁡ x → 1 + sin ⁡ − 1 ( 2 x 1 + x 2 ) ≠ lim ⁡ x → 1 − sin ⁡ − 1 ( 2 x 1 + x 2 ) \displaystyle\begin{aligned}\lim_{x\to1^+} \dfrac{f(x)-f(1)}{x-1}&=\lim_{h\to0^+}\dfrac{f(1+h)-f(1)}h\\&=\lim_{h\to0^+}\dfrac{\pi-2\tan^{-1}(1+h)-2\tan^{-1}(1)}h\\\text{Using L'Hôpital's rule }&=\lim_{h\to0^+}\dfrac{-2}{(1+h)^2+1}\\&=\boxed{-1}\\\\\lim_{x\to1^-} \dfrac{f(x)-f(1)}{x-1}&=\lim_{h\to0^-}\dfrac{f(1-h)-f(1)}{-h}\\&=\lim_{h\to0^-}\dfrac{2\tan^{-1}(1-h)-2\tan^{-1}(1)}{-h}\\\text{Using L'Hôpital's rule }&=\lim_{h\to0^-}\dfrac{-2}{-1\cdot\left[(1-h)^2+1\right]}\\&=\boxed{1} \\\\\Rightarrow \lim_{x\to1^+}\sin^{-1}\left(\dfrac{2x}{1+x^2}\right)&\ne \lim_{x\to1^-}\sin^{-1}\left(\dfrac{2x}{1+x^2}\right)\end{aligned}

Thus, it is not differentiable at x = 1 x = 1 , nor at x = − 1 x=-1

We can say this just by looking at the graph of sin ⁡ − 1 ( 2 x 1 + x 2 ) \sin^{-1}\left(\dfrac{2x}{1+x^2}\right)

At x = 1 x=1 , the graph has a sharp edge and thus the function is not differentiable at x = 1 x = 1

6 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Your first explanation doesn't work. You are assuming that the derivative of a function must be continuous, which is not necessarily true. There isn't a reason to evaluate lim ⁡ x → 1 f ′ ( x ) \lim_{x \rightarrow 1 } f'(x) in order to determine if f ′ ( 1 ) f'(1) exists.

Instead, what we have is that f ′ ( 1 ) = lim ⁡ x → 1 f ( x ) − f ( 1 ) x − 1 f'(1) = \lim_{x \rightarrow 1 } \frac{ f(x) - f(1) } { x - 1 } . It is this limit where the left-hand limit and the right-hand limit are different, which is why f ′ ( 1 ) f'(1) doesn't exist.

The second and third explanations work, because they are considering lim ⁡ x → 1 f ( x ) − f ( 1 ) x − 1 \lim_{x \rightarrow 1 } \frac{ f(x) - f(1) } { x - 1 }

@Calvin Lin , Yes, I thought this same thing at school today... And now you said it! Thanks Sir!

Kishore S. Shenoy - 5 years, 8 months ago

So, if we take f ′ ( 1 ) = lim ⁡ x → 1 f ( x ) − f ( 1 ) x − 1 f'(1) = \lim\limits_{x \to 1 } \frac{ f(x) - f(1) } { x - 1 } , what we get is method 3 right? So can I delete method 1 (which is wrong)?

Kishore S. Shenoy - 5 years, 8 months ago

Log in to reply

Actually, looking at method 3 again, it doesn't work for the same reason. What you are calculating is lim ⁡ x → 1 f ′ ( x ) \lim_{ x \rightarrow 1 } f'(x) , which may not be equal to f ′ ( 1 ) f' (1) .

And of course, method 2 via "inspection of graph" isn't a proof per se.

Calvin Lin Staff - 5 years, 8 months ago

Log in to reply

I can correct the third method. But correcting the first method brings me to the corrected 3rd one...

Kishore S. Shenoy - 5 years, 8 months ago

Are you able to figure out why the derivative of a differentiable function need not be continuous? If so, please add a solution

Calvin Lin Staff - 5 years, 7 months ago

Log in to reply

Yes! I will add a solution. Had tests these days. I'll post a solution today. Sorry for the delay...

Kishore S. Shenoy - 5 years, 7 months ago

I think that should do it @Calvin Lin sir...

Kishore S. Shenoy - 5 years, 7 months ago
Surya Prakash
Oct 8, 2015

GENERAL MISTAKE:

Take x = tan ⁡ θ x=\tan{\theta} ⟺ \iff θ = arctan ⁡ x \theta = \arctan{x} .

So, arcsin ⁡ ( 2 x 1 + x 2 ) = arcsin ⁡ ( 2 tan ⁡ θ 1 + tan ⁡ 2 θ ) = arcsin ⁡ ( sin ⁡ 2 θ ) = 2 θ = 2 arctan ⁡ x \arcsin \left(\dfrac{2x}{1+x^2} \right) = \arcsin \left( \dfrac{2 \tan{\theta}}{1+ \tan ^2 \theta} \right) = \arcsin \left( \sin 2\theta \right) = 2 \theta = 2 \arctan{x}

d d x arcsin ⁡ ( 2 x 1 + x 2 ) = d d x 2 arctan ⁡ x = 2 1 + x 2 \dfrac{d}{dx} \arcsin \left(\dfrac{2x}{1+x^2} \right) = \dfrac{d}{dx} 2 \arctan{x} = \dfrac{2}{1+x^2}

Therefore,

d d x [ arcsin ⁡ ( 2 x 1 + x 2 ) ] x = 1 = 1 \dfrac{d}{dx} \Bigg[\arcsin \left( \dfrac{2x}{1+x^2} \right) \Bigg]_{x=1} = 1

But this is actually W R O N G \color{#D61F06}{WRONG} .

CORRECT METHOD:

Let us see what happens if we bash this problem directly.

Let f ( x ) = arcsin ⁡ ( 2 x 1 + x 2 ) f(x) = \arcsin \left( \dfrac{2x}{1+x^2} \right)

f ′ ( x ) = d d x [ arcsin ⁡ ( 2 x 1 + x 2 ) ] = 1 1 − ( 2 x 1 + x 2 ) 2 × d d x ( 2 x 1 + x 2 ) = 1 + x 2 ∣ 1 − x 2 ∣ × 2 ( 1 − x 2 ) ( 1 + x 2 ) 2 \begin{aligned} f'(x) &= \dfrac{d}{dx} \Bigg[\arcsin \left( \dfrac{2x}{1+x^2} \right) \Bigg] \\ &= \dfrac{1}{\sqrt{1-\left(\dfrac{2x}{1+x^2} \right)^{2}}} \times \dfrac{d}{dx} \left(\dfrac{2x}{1+x^2} \right) \\ &= \dfrac{1+x^2}{|1-x^2|} \times \dfrac{2(1-x^2)}{(1+x^2)^2} \end{aligned}

What actually this says?? This says that the derivative of f ( x ) f(x) does not exist at x = 1 x=1 .

Be careful while calculating the derivatives using substitution method.

3 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Interesting question. Unfortunately, your analysis has several holes.

  • In General mistake , you mistakenly claim that a r c s i n ( sin ⁡ 2 θ ) = 2 θ arcsin ( \sin 2 \theta ) = 2 \theta . See Inverse Trig puzzle for why this is not true. This explains why you obtained an incorrect answer using this method.

  • Derivative using substitution method x = g ( θ ) x = g (\theta) is valid, as long as the substitution used is a differentiable function in the neighborhood, and g ′ ( θ ) ≠ 0 g'( \theta ) \neq 0 . This follows from the chain rule:

f ∘ g ( θ ) g ′ ( θ ) = f ′ ∘ g ( θ ) ) \frac{ f \circ g ( \theta ) } { g' ( \theta ) } = f' \circ g ( \theta ) )

  • The continuity of f ′ ( x ) f'(x) at x = 1 x = 1 is irrelevant to the existence of f ′ ( 1 ) f'(1) . You have not yet shown that f ′ ( 1 ) f'(1) does not exist.

  • The correct way to approach this, would be to use first principles, and show that the left-hand limit is 1, and the right-hand limit is -1, which is why the function isn't differentiable at 1 since the limits are not equal.

Interesting question, but your analysis of the problem is flawed.

Calvin Lin Staff - 5 years, 8 months ago

Log in to reply

is it possible to get a genralised result of differentiation of a factorial

Jaswinder Singh - 5 years, 8 months ago

Log in to reply

Jaswinder Singh there is general result of differentiation of factorials. Differentiation of gamma function. Γ a ( x ) = ∫ 0 ∞ ( t x − 1 ( l n t ) a e − t ) d t . { \Gamma }^{ a }\left( x \right) =\int _{ 0 }^{ \infty }{ \left( { t }^{ x-1 }{ \left( lnt \right) }^{ a }{ e }^{ -t } \right) dt. }

Aditya Kumar - 5 years, 8 months ago

I think the limit exists because at x = 1 x = 1 , arcsin ⁡ ( sin ⁡ 2 θ ) = 2 θ = 2 arctan ⁡ x \arcsin(\sin 2\theta)= 2\theta= 2\arctan x

sin ⁡ − 1 ( 2 x 1 + x 2 ) = { − π − 2 tan ⁡ − 1 x x < − 1 2 tan ⁡ − 1 x x ∈ [ − 1 , 1 ] π − 2 tan ⁡ − 1 x x > 1 \sin^{-1}\left(\dfrac{2x}{1+x^2}\right) = \begin{cases}-\pi-2\tan^{-1}x&x<-1\\ 2\tan^{-1}x&x\in[-1,1]\\\pi-2\tan^{-1}x&x>1\end{cases}

See the graph

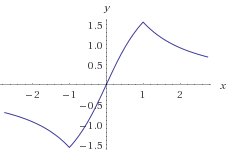
So, the answer will be 1.

Kishore S. Shenoy - 5 years, 8 months ago

Log in to reply

You drew the graph of sin ⁡ − 1 2 x 1 + x 2 \sin^{-1} \frac{2x}{1+x^2}

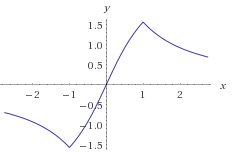
From this, we can conclude that the limit lim ⁡ x → 1 sin ⁡ − 1 2 x 1 + x 2 \lim_{x \rightarrow 1} \sin^{-1} \frac{2x}{1+x^2} exists and is equal to π 2 \frac{\pi}{2} .

Furthermore, by looking at the slopes of the limiting tangents, the limit lim ⁡ x → 1 d d x ( sin ⁡ − 1 2 x 1 + x 2 ) \lim_{x \rightarrow 1}\frac{d}{dx} \left( \sin^{-1} \frac{2x}{1+x^2} \right) does not exist. From the LHS, the limit is 1. From the RHS, the limit is -1. Hence, the function isn't differentiable at x = 1 x = 1 .

Calvin Lin Staff - 5 years, 8 months ago

Log in to reply

@Calvin Lin – I get it, I get it. So, what shloud be the answer?? "Limit does not exist"??

Kishore S. Shenoy - 5 years, 8 months ago

Log in to reply

@Kishore S. Shenoy – I would simply go with "does not exist" or "the differential does not exist"

Can you post a solution to this problem? Thanks!

Calvin Lin Staff - 5 years, 8 months ago

sir I don't agree with you, you are suppose to simplify the expression before substitution. and I don't think that |1-x| is the same as ((1-x)^2)^1/2 like wot u assumed

Benjamin ononogbu - 5 years, 8 months ago

Little mistake. If a function is not differentiable at x = a x=a doesn't mean it is not continious at that point, for example f ( x ) = ∣ x ∣ f(x)=|x| at x = 0 x=0

Hjalmar Orellana Soto - 5 years, 8 months ago

Log in to reply

No it is not like that.

Aditya Kumar - 5 years, 8 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...