I don't like pizza crust
Is it possible to cut a circle into pieces with these conditions?
- There are finitely many pieces.
- The pieces must be congruent , meaning that they have the same shape and area.
- Some of the pieces have at most one point on the circumference of the circle.
- Curved cuts are allowed.
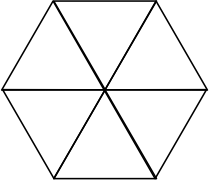
This cutting is only
partially
correct. It satisfies all but the "same shape" condition.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Moderator note:
This is from the comments, but is worth putting here:
Here's a way to think about this problem. Start with a circle divided into 6 sectors:
You can almost obtain the solution by dividing each of these sectors in half in this way:
However, these shapes aren't all congruent. They would need to be curved on all sides in order to be congruent. We can accomplish this by putting arcs on each of the straight segments of each sector:
Each of these "curved sectors" consist of three congruent 6 0 ∘ arcs. And so, each of the "curved sectors" is congruent. If we split them in half (as we tried before with the normal sectors), we will obtain 12 congruent shapes within the circle.
It's also possible to cut the circle so that some of the pieces have no points on the circumference of the circle.
I'm still looking for a complete solution, and find it weird that nobody has given one yet, or has given an otherwise convincing proof that it exists. In my opinion, the easiest proof would be a solution, with possibly proof that the pieces are indeed identical.
Probabaly indeed mirror images are required, in which case the problem could be clarified.
Log in to reply
I think “congruent” allows mirror images. https://en.m.wikipedia.org/wiki/Congruence_(geometry)
Rule was atmost one point per piece on the circumference.
Log in to reply
"Some of the pieces have at most one point", which means that some of the pieces may have more than one point. The solution holds.
Log in to reply
Then why cut it at all? Leave it be and it fulfills all of the criteria.
Log in to reply
@Caspian Berggren – If it were all one piece, it would fail to meet the criterion that some of the pieces have at most one point of contact with the perimeter. The problem requires there to be cuts.
How do u prove that the area of the figures are equal???
Log in to reply
The 5th image in this solution helped me understand this, the blue lines divide the six equal sections created by the curved lines placed at equal 30-degree rotations.
Here's a way to think about this problem. Start with a circle divided into 6 sectors:
You can almost obtain the solution by dividing each of these sectors in half in this way:
However, these shapes aren't all congruent. They would need to be curved on all sides in order to be congruent. We can accomplish this by putting arcs on each of the straight segments of each sector:
Each of these "curved sectors" consist of three congruent 6 0 ∘ arcs. And so, each of the "curved sectors" is congruent. If we split them in half (as we tried before with the normal sectors), we will obtain 12 congruent shapes within the circle.
It's also possible to cut the circle so that some of the pieces have no points on the circumference of the circle.
Log in to reply
This is a basic-level question?
A really interesting visualization!!!!
This is even more beautiful than the solution I posted. Makes you think of a rose.
I enjoy the flower-like nature of all these solutions. That last one is pretty complex, though!
This was my intended solution. The original wording had 'there exists a piece not touching the circumference' I think. Oh well, it's still a good problem.
I don't understand rule no. 3. Here all the shapes in the outside edge has more than one point on the circumference. If this is allowed then why can't just cutting it like a pizza (1st figure) be allowed.
Log in to reply
You can cut it up like a pizza... if you can figure out a way to have at least one piece somewhere that only touches the circumference at one point. Andrew Hayes has given an example where some pieces do not touch the circumference at all, but that doesn't meet rule 3.
Log in to reply
@Michael Mendrin – The second solution, where some pieces don't touch the circumference at all, does meet rule three (as it is phrased currently). The pieces in the inside can be said to touch the circle at at most one point, because 0 points is less than 1 point.
Another way to write the problem that would rule out simply cutting it like a pizza would be to make rule 3: "Some of the pieces touch the circumference at a finite number of points." I wonder what a solution that satisfies this rule and not the actual rule (i.e. a solution in which some pieces touched the circumference at more than 1 but a finite number of points) would look like? (or if its possible?)
Log in to reply
@Grady Crossley – Okay, you are right, very confusing. Then Andrew has provided the most elegant solution. As for a finite number of points.....whew!
Some of the pieces have at most one point on the circumference of the circle. It's not necessary that all of the pieces have this property.
When you cut a circle in half, then there are two semi circles. These semi circles do not have any points on the circle, because there is no circle left. If you would divide the circle in pieces and leave the circle intact, then that is a different question.
Respected Sir and everyone , Please excuse me for posting this comment . Rather than saying that this is a comment this a burning issue in my heart . Please take it seriously .
I have a dream getting 100 or more up votes for an individual solution . I wrote a solution for the question water shadows (which is adjacent to this question) 6 days ago (on 21 April) . When I wrote the solution I thought it is a good one and will definitely accomplish my dream .
I am extremely happy when I saw that the question is in one of the problems of the week . I thought I am nearer to my dream because nobody posted any solution at that time expect me to this question and my solution is a clear and good one . But after these four days I am extremely sad because even more than 11,000 people solved that question only 83 people are discussing solutions . As a result at present I am only left now with 45 up votes . Although my solution deserves more than 100 up votes due silly reasons it is unable to accomplish my dream .
At first when I solved this question (infinite squares) on Monday morning I solved in the manner you did . I thought to post the solution but when I saw you have already posted the same solution (and now you got 299 up votes) . But I didn't worry at that time because I had hope that my solution to water shadows question will definitely cross 100 up votes .
Once see the up votes to the top solutions for the 5 questions of the problems of this week and see how odd it looks :
Infinite squares - Jason Dyer - 349 up votes
Water shadows - Ram Mohith - 57 up votes (see how odd it looks)
Third problem - Zain Majumder - 167 up votes
Fourth problem - Jeremy Galvagni - 129 up votes
Fifth problem - Micheal Mendrin - 250 upvotes
My point is that please try to discuss solutions to every question you solved and try to up vote the solution you admire as much as possible . If you do that many people like me will acheive what they deserve .
Please try to understand my problem .
Log in to reply
Ram Mohith, most of the time I only get less than 10 votes, often none at all. This time I got lucky and bagged over 250 votes. Let me offer you some tips on how to bag over 100 votes for a solution you post:
1) Pick the easy problems, because those are seen by many more people than harder ones
2) Try to be the first to post a solution to it (yes, I know you've tried that)
3) Using illustrative graphics really helps catch attention
4) Be a Brilliant Staff member...well, okay, that one is hard to do, but that definitely helps
When people click to see the solution(s), and if the first thing they see is something that they can immediately grasp (again, illustrative graphics really helps), they are much more likely to upvote it just as quickly. Then votes build up.
I know of a good number of really excellent mathematicians here that have posted very long and complex solutions, requiring a lot of time and effort to craft, and yet they often only get a vew upvotes. That's because often only a few even try the problem or look up the solutions. Nevertheless, it gives them satisfaction that their peers are reading them.
Log in to reply
Ok. Thanks for you guidelines
Actually I am not worrying about my up votes . I am saying that people who deserve more up votes are not achieving that because less number of people are discussing the solutions .
Ram, you really need to stop posting this spam comment on every question.
@Moderators, can you delete these spammy posts by Ram that are showing up all over the site?
One of the great things about Brilliant has always been that its 3 million users don’t spam the comments. Until now..... Seriously. Unlike a news website, the comment/solution section of Brilliant is a key part of the content.
Log in to reply
I just want to bring to notice that many solutions which deserve many upvotes are getting only few upvotes just because no one are discussing the solutions.
You totally misunderstood the inner meaning of my comment and called it as spam. If I posted the above comment in only one question only people discussing to that qiestion only will see it. Do you that the response for this comment is huge. After I kept the above comment many people understood my problem and they started to discuss the solutions and upvote them and many good solutions are getting what they deserve.
You will know the power of that comment only when you write a perfect solution but no upvotes are coming just beccause pepole are not disscusing that question. You will undergo the same fire in your heart.
Those who went through this fire in their heart (like Micheal Mendrin) support for this comment. You didn't write any solution so far so there is no word of upvotes and hence you are unable to understand the inner meaning of my comment.
Respected sir, you are elder to me in age and should have much more experience than me in life. But your above comment on me is not justified. Please excuse me sir for speaking against you like this.
I always speak like this because I will always read inspirational books and I am bit emotional too. Sorry sir for this comment.
Such an amazing solution. I was inspired to do a Desmos animation of it spinning, since it reminds me of a flower pinwheel. Here's the link if anyone wants to see it in motion. (Haven't tried to make the no point solution spin). https://www.desmos.com/calculator/chp34lodv3
But no curved cuts were allowed
Log in to reply
The condition says "Curved cuts are allowed". Please read the question carefully.
I too got it wrong
That last figure really looks like dark magic. You should definitely be careful with these :O
I don't exactly understand the question. Could someone please explain it to me. Couldn't we just cut it up in 4 quarters?
Because of rule 3. "Some of the pieces have at most one point on the circumference of the circle." Cutting into 4 quarters would mean ALL pieces would be touching the circumference at more than one point. There needs to be at least one piece that only touches the circumference at a singular point.
that's what I thought at first, but then there would be no pieces with "at most one point of the circumference", although there have to be "some" (condition 3)
Any piece not touching the circumference at all fulfils rule 3 (touches at most once).
1.finitely 2.congruent 3.some pieces only have one or zero point on the circle. 4.curved cuts are allowed.
It's the 3rd condition that prevents cutting into quarters from being a solution. Some of the pieces are required to only touch the circumference AT MOST at a single point.
If you just cut it in half, thirds, quarters etc, none of the pieces will satisfy the 3rd condition as they all will have some arc length of the circumference as a part of their shape, which is much more than only a point.
It is true that as the number of slices you divide approaches infinity, the arc length approaches a point. However, condition 1 forces us to keep our number of pieces finite. Hopefully this helps.
Log in to reply
Ah, yes, I was simply thinking of the chord being the "shape."
In that case, I vote we cut the circle into gingerbread people, with one of the people being on the circumference.
Can't do that. Only one point of the cut up shape can touch the circumference of the circle. So, no quartering the circle, please. 😜
My solution use only curves: https://sumopaint.com/images/temp/xzsxgemfjadgtbgj.png
(It looks like some commenters are uploading drawings? I don't see how to do that, thus the link. Or is that only moderators?)
question states At Least One corner touching the circumference.. cut like a normal pizza... (if not, question is written wrong)
The Yin and Yang symbol doesn't work for the same reason that a line drawn straight through the diameter of the circle wouldn't. Rule 3 states that "Some of the pieces have at most one point on the circumference of the circle." This means at least one slice must have only one point on the circumference of the circle. The Yin Yang symbol has two slices, both of which touch the circle at more than one point, invalidating the solution.
This clearly fails to satisfy the third condition. Read the problem!
I just cut it in half! What's the problem!
Log in to reply
Some of the pieces have at most one point on the circumference of the circle.
fails on rule 3
'No curved cuts' makes only simple solutions possible. The set of radial-only cuts with n = 2, 3, 4 ... pieces is all I could think of.
The last rule is "curved cuts ARE allowed".
How did you add an image to your comment? I couldn't figure out how to do that.
Please clarify this statement: “Some of the pieces have at most one point on the circumference of the circle.”
Does it mean, regarding points on the circumference, that all of these are possible: some pieces have only one point (“at most one”), some have no points (less than “at most one”), and some pieces have more than one (not THOSE pieces with at most one point).
Sounds like nothing is excluded.
Considering that the pieces can only have one point, that rules out quarters, but you can use any regular geometric shape and curve the sides.
a swirl circle, cutting each line thin to not recognize the curves on the side?
In order to cut pieces so thin that curves are "not recognize"-able, one would require infinitely many pieces.
Matt Parker's book explains this
The "some of the pieces at most" part is a bit confusing. Based on the example solution, it seems like a trivial requirement, but the wording makes it sound like it's supposed to be important.
Can't we just cut the circle up like a pie indefinitely?
Note: Congruent shapes can be mirror images of each other.