I don't think I can do it 4
Calculate the area bounded by the lines x = y 2 − 2 y , x + y = 0 .
If the area is A 1 sq. units. Find the positive integer A .
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
sir,can you explain the idea of swapping variables here?
Log in to reply
You can also do it without swapping as follows:
A = ∣ ∣ ∣ ∣ ∫ 0 1 ( y 2 − 2 y ) d y − ∫ 0 1 ( − y ) d y ∣ ∣ ∣ ∣
You will get the same result, obviously. I just swapped them, so that I could draw the graph easily.
Swapping d x to d y gives an easier solution. Otherwise, you have to do ∫ − 1 0 ( 1 − x + 1 ) d x as Aareyan has done.
Log in to reply
i meant that why do we do "dy". is it some rule i am unaware of.
Log in to reply
@Aareyan Manzoor – As I have mentioned, it is easy to evaluate ∫ 0 1 ( y 2 − 2 y ) d y than ∫ − 1 0 ( 1 − x + 1 ) d x and you get the same result.
without swapping variables:
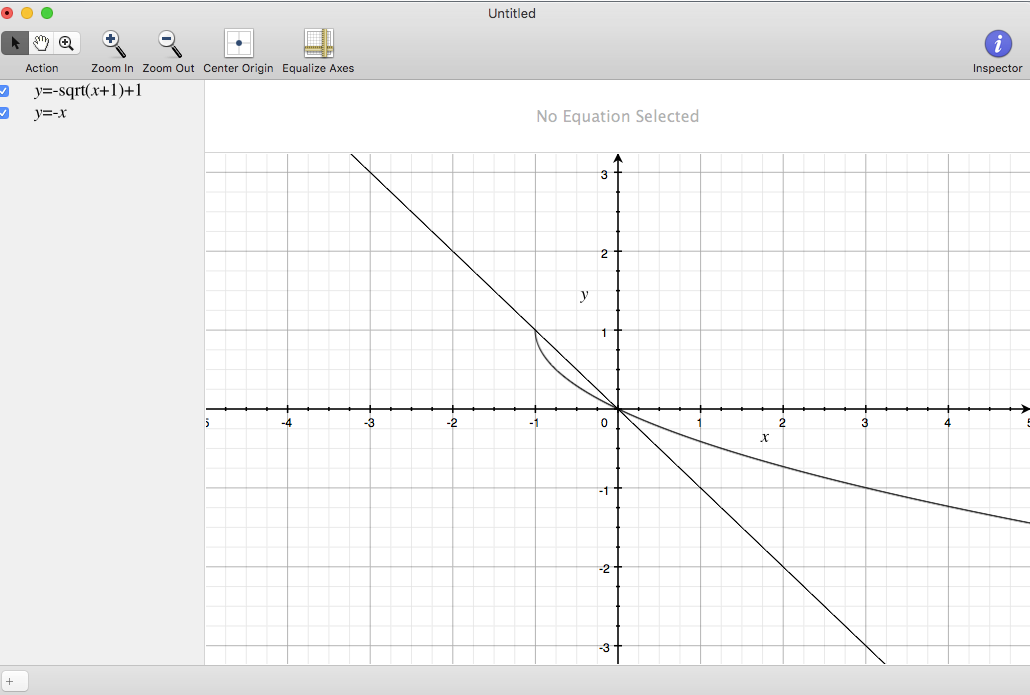
 for the required area, the bounds are -1,0. and the equation
x
=
y
2
−
2
y
⟹
y
2
−
2
y
+
1
=
x
+
1
⟹
y
=
±
x
+
1
+
1
obviously for the required range
y
=
−
x
+
1
+
1
.
for the required area, the bounds are -1,0. and the equation
x
=
y
2
−
2
y
⟹
y
2
−
2
y
+
1
=
x
+
1
⟹
y
=
±
x
+
1
+
1
obviously for the required range
y
=
−
x
+
1
+
1
.
 now we just integrate:
∣
∣
∣
∣
∫
−
1
0
(
−
x
+
1
+
1
)
d
x
−
∫
−
1
0
(
−
x
)
d
x
∣
∣
∣
∣
∣
∣
∣
∣
∣
∣
∣
⎣
⎢
⎡
−
2
3
(
x
+
1
)
3
/
2
+
x
⎦
⎥
⎤
−
1
0
−
[
−
2
x
2
]
−
1
0
∣
∣
∣
∣
∣
∣
∣
∣
∣
∣
∣
3
1
−
(
2
1
)
∣
∣
∣
∣
=
6
1
now we just integrate:
∣
∣
∣
∣
∫
−
1
0
(
−
x
+
1
+
1
)
d
x
−
∫
−
1
0
(
−
x
)
d
x
∣
∣
∣
∣
∣
∣
∣
∣
∣
∣
∣
⎣
⎢
⎡
−
2
3
(
x
+
1
)
3
/
2
+
x
⎦
⎥
⎤
−
1
0
−
[
−
2
x
2
]
−
1
0
∣
∣
∣
∣
∣
∣
∣
∣
∣
∣
∣
3
1
−
(
2
1
)
∣
∣
∣
∣
=
6
1
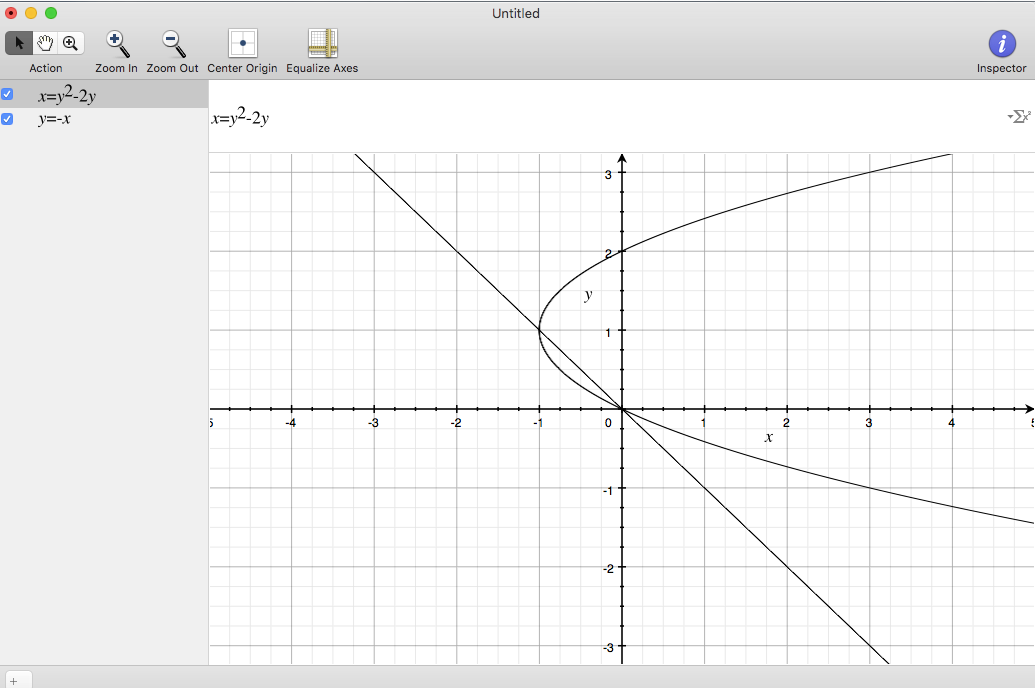
Without loss of generality, swap variable x with y , then we have: { y = x 2 − 2 x y = − x .
We note that the area is bounded within 0 ≤ x ≤ 1 (see graph). Therefore, the area is given by:
A = ∣ ∣ ∣ ∣ ∫ 0 1 ( x 2 − 2 x ) d x − ∫ 0 1 ( − x ) d x ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ ∣ [ 3 x 3 − x 2 ] 0 1 − [ − 2 x 2 ] 0 1 ∣ ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ − 3 2 + 2 1 ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ − 6 1 ∣ ∣ ∣ ∣ = 6 1
⇒ A = 6