Mechanics + Magnetism = Mechatism 2
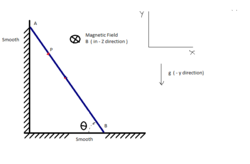 Let an
conducting Thin Rigid Rod
of Length 'L' and mass 'm' is released under gravity from rest at time t=0 at an angular position
θ
0
=
6
0
0
from horizontal.
Let an
conducting Thin Rigid Rod
of Length 'L' and mass 'm' is released under gravity from rest at time t=0 at an angular position
θ
0
=
6
0
0
from horizontal.
There is gravity in -Y direction and uniform Magnetic Field of strength B 0
The Rod is sliding on the perfectly smooth Surface.
So Find the Magnitude of Motional EMF produced in Rod between The End Point A and Point P at the instant when Rod is making an angle θ = 3 0 0 from Horizontal.
Let your answer is α Then Evaluate ⌊ 1 0 0 α ⌋ .
Details
∙ A P = 4 1 m ∙ L = 1 m ∙ B = 1 T ∙ g = 1 0 m / s 2 .
This is part of set Mixing of concept Click here
This is Original
The answer is 51.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
So actually cosine law was the law one has to use while solving for OP.
it can also be solved by taking an elementary component between A and P and finding its velocity perpendicular to length and then integrating it,, i originally solved it that way, but then i saw your method and it was much better than my complicated way,,, but its funny how we can imaginarily attach cells to different points even though there is no rod connecting A or P to O,
Log in to reply
You mean after calculating angular velocity about ICR ??
Log in to reply
yes or by taking it as combined translation and rotation of com
Log in to reply
@Mvs Saketh – You mean in this way ∫ d E = ∫ B ( d l ) V ⊥ . nice...it is also good approach..!!
Log in to reply
@Deepanshu Gupta – Here do i need to integrate at OA and OP separate from t=0 to t=t? Can you please put the solution that way (bit slow in integration )
Log in to reply
@Ashwin Gopal – No if You want to integrate Then it is useless for integrating OA and OP seprately becoz it gives same Result (Since Potential difference is independent of reference frame)
instead of this You Integrate for AP
(but it also Lengthy So Best Technique for such type Question is By Evaluting Potential difference B/w two Hypothetical Rods as I showed above )
Log in to reply
@Deepanshu Gupta – you neglected that the rod moves to the right with speed v ????!!!!
As we consider ICR for converting the problem from rotation and translation ,is there any concept for converting it to translation only?
ohh .. really nice method . i had un-neccesserily integrate it . But your approach is really cool !
How can we just use energy conservation?? Isn't the total energy= The kinetic energy of the rod+ the heat generated in the rod due to current flow??? Why are we neglecting the latter one? But surprisingly, if we follow the ICR method, it does lead to the ans where the current generated heat has been neglected. This is highly surprising.
Wow! That's a really nice way to calculate the induced emf between A and P!
So, there's going to be a current flowing through this rod, and there's a magnetic field, so there's going to be a force on the rod as a result of that. It's not obvious to me why the net torque due to this is 0. Would you care to elaborate?
Instead of a trick with ICR of the rod I'll use a lagrangian to derive equations of motion.
Let A = ( 0 , y ) and B = ( x , 0 ) be coordinates of points A and B . We easily observe that x 2 + y 2 = l . A point P on a rod such that ∣ A P ∣ = λ l ( 0 ≤ λ ≤ 1 ) has coordinates P = ( λ x , ( 1 − λ y ) ) . Therefore, its velocity vector v ( λ ) has coordinates v ( λ ) = ( λ x ˙ , ( 1 − λ ) y ˙ ) . So the kinetic energy T has value T = 2 m ∫ 0 1 ( λ 2 x ˙ 2 + ( 1 − λ ) 2 y ˙ 2 ) d λ = 6 m ( x ˙ 2 + y ˙ 2 ) . Now, we take x = l cos θ and y = l sin θ . This gives us x ˙ = − l t h e t a ˙ sin θ and y ˙ = l θ ˙ cos θ . So we have T = 6 m l 2 θ ˙ 2 . Potential energy V of rod is equal to V = 2 1 m g l sin θ . So the lagrangian L is L = 6 m l 2 θ ˙ 2 − 2 1 m g l sin θ This gives us equation of motion 3 m l 2 θ ¨ = − 2 1 m g l cos θ . Now we use θ ¨ = θ ˙ d θ d θ ˙ which yields 3 m l 2 ∫ 0 ω θ ˙ d θ ˙ = − 2 1 m g l ∫ 3 π 6 π cos θ d θ . After this computation we get ω = 2 l 3 g ( 3 − 1 ) .
Since each point on the rod has velocity v ( λ ) = ( − λ l θ ˙ sin θ , ( 1 − λ ) l θ ˙ cos θ ) its velocity v ⊥ ( λ ) is equal to v ⊥ ( λ ) = ∣ − λ l θ ˙ sin 2 θ + ( 1 − λ ) l θ ˙ cos 2 θ ) ∣ . Now it suffice to take d E = B l v ⊥ ( λ ) , and substitute θ = 6 π , θ ˙ = ω and calculate E A P = B l ∫ 0 4 1 v ⊥ ( λ ) d λ = 3 2 5 B l 2 2 l 3 g ( 3 − 1 ) .
As Shown in figure 'O' is ICR ( Instantaneous centre of rotation ) About This Point motion of rod is Pure Rotatory .
So for calculating Torque about 'O' is only due to m g sin θ . component since all other components Do not create Torque.
τ 0 = I 0 α m g sin θ 2 L = ( 1 2 m L 2 + 4 m L 2 ) α α = 2 L 3 g sin θ − ω d θ d ω = 2 L 3 g sin θ ∫ 0 ω ω d ω = − 2 L 3 g ∫ 6 0 0 3 0 0 sin θ d θ ω = 2 L 3 g ( 3 − 1 ) ⟶ ( 1 ) .
NOTE
( You Can Also Use Energy conservation For Calculating angular velocity )
Now For Calculating EMF Between A & P We Calculate emf 's between OA and OP & then Subtract them to get emf between A & P since They are connected in Series with opposite Polarity
E O A = 2 B ω ( l O A ) 2 = 2 B ω ( L cos ( 3 0 0 ) ) 2 = 8 3 B ω ( L ) 2 E O P = 2 B ω ( l o p ) 2 = 3 2 7 B ω ( L ) 2 E A P = E O A − E O P E A P = 3 2 5 B ω ( L ) 2 ⟶ ( 2 ) .
For calculation Of OP see below
Now Putting all value in 2 equation we get
E A P = 3 2 5 B ( L ) 2 2 L 3 g ( 3 − 1 ) = 0 . 5 1 7 7 1 4 ⌊ 1 0 0 α ⌋ = 5 1 A n s . .
Note : For Calculation Length of OP we use Cosine Law in triangle OCP at the instant of time when angle is 30 degree from horizontal as shown in figure below.
cos 1 2 0 0 = 2 ( 2 L ) ( 4 L ) ( 2 L ) 2 + ( 4 L ) 2 − ( O P ) 2 ⇒ O P 2 = 1 6 7 L 2 .