Identical Charges are corrected
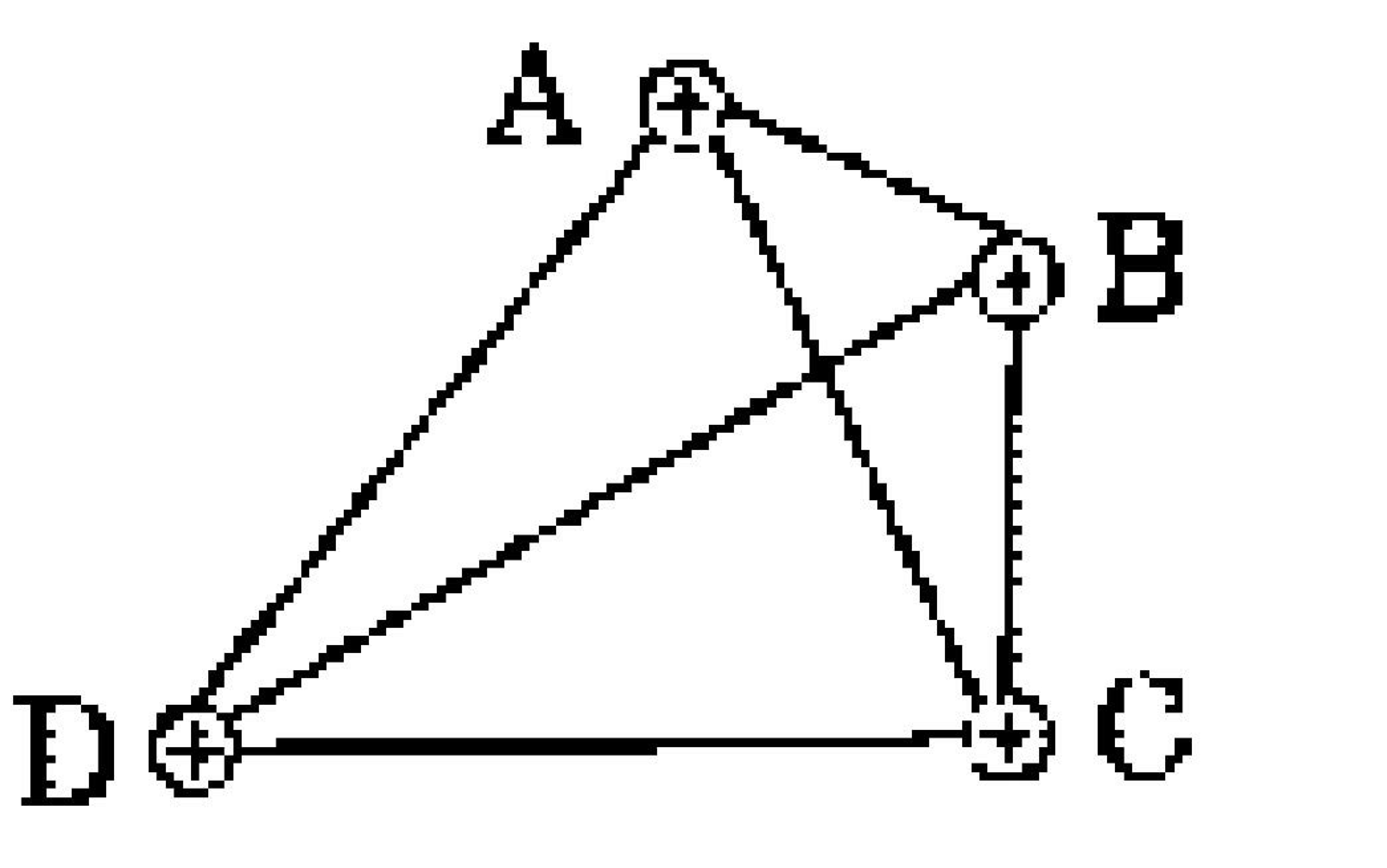 Four identical particles
A
,
B
,
C
and
D
each of massn
m
and charge
q
are connected by insulating light inextensible threads of equal length
l
make a tetrahedron as shown in the figure.
Four identical particles
A
,
B
,
C
and
D
each of massn
m
and charge
q
are connected by insulating light inextensible threads of equal length
l
make a tetrahedron as shown in the figure.
The thread connecting particles
A
and
B
is cut.
Find maximum speed acquired by every particle in subsequent motion.
And then add up that alll maximum speeds for the final answer
Final Answer comes in the form of
α
π
ϵ
0
m
l
q
2
Type
α
=
?
Thanks to Mark sir for correcting the problem.
The answer is 0.946.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
@Mark Hennings Thanks for the solution.
@Mark Hennings
Sir can you please help me in this problem, whenever you will be free.

Thanks in advance
Log in to reply
A normal reaction and a friction force act on the mass, and their equal and opposite reactions act on the block. We need to assume that the block is uniform, and that its centre of mass is at the centroid of the triangle. The normal reaction force on the wedge gives a clockwise moment about the bottom right corner of the wedge, while the friction force and the weight give anticlockwise moments about the bottom right corner of the wedge. In order not to topple, the overall moment should be anticlockwise. Now you finish off...
Hi Lil Doug. I am Pradeep. Your thoughts are exactly similar to me. Could you tell me your JEE MAINS rank?
Log in to reply
@dishantha praddep I am currently in class 12 studying. I will give Jee Mains in 2021.
Can you tell what is the ans?
@Mark Hennings
Sir can you please help me in this problem, whenever you will be free.

Thanks in advance
Log in to reply
@Mark Hennings this above one is solved right now
See, the initial tension on thread A is 4mg/3 and final tension is 3mg.
Log in to reply
@Pradeep Tripathi
I solved it.
Solve the problem below one. And what is your rank.?
Log in to reply
@Talulah Riley – Rank is 2932.
Log in to reply
@Pradeep Tripathi
–
@Pradeep Tripathi
can you tell marks distribution?
By the way. My chemistry subject is extremely weak.
Log in to reply
@Talulah Riley – Dude, rank is all about percentile. In Jan, I got 99.7496367 and in Sept. 99.6318234
Log in to reply
@Pradeep Tripathi – @Pradeep Tripathi Can you predict your marks?
Log in to reply
@Talulah Riley – 216 and 238 in 300. Why don't you tell about yourself?
Log in to reply
@Pradeep Tripathi – @Pradeep Tripathi what do you want to know about me?
Log in to reply
@Talulah Riley – Nothing , just a kind of time pass! That's my nature.
Log in to reply
@Pradeep Tripathi – @Pradeep Tripathi How do you studied chemistry ? I haven't studied chemistry of class 11 till now.
Log in to reply
@Talulah Riley – Maintain your rhythm. Its your fault that you didn't studied chemistry. You have to think about this ,yourself. I can't help you in it.
Log in to reply
@Pradeep Tripathi
–
@Pradeep Tripathi
I haven't studied organic only.
Inorganic and physical chemistry are at a good level.
I am planning to give exams without organic, I can easily secure full marks in Phy and math.
Log in to reply
@Talulah Riley – Then study organic at this instant . Don't waste your time. Stop disturbing me, please.
Log in to reply
@Pradeep Tripathi – @Pradeep Tripathi I will not study organic, I will exam without that only. And I am not disturbing you, first you started texting message me.
@Mark Hennings sir in this one also ,it feels me that I am disturbing you. Sorry,you can upload solution whenever you will be free
And one more thing,if you don't mind,you can post solution using pen and page also,if it takes time to type with Latex.

Log in to reply
The total frictional force around the disc of contact exerts a moment μ M g r about the vertical axis of the sphere, where M is the mass of the sphere and r is the radius of the hole. Thus the rotational equation of motion of the sphere is 5 2 M R 2 ω ˙ = − μ M G r so that ω ˙ = − 2 R 2 5 μ g r for 0 < r < R . Thus the time to come to rest from initial angular speed ω 0 is T = 5 μ g r 2 ω 0 R 2 ∝ r − 1 Since T = 9 seconds when r = 8 cm, we deduce that T = 1 2 seconds when r = 6 cm.
Log in to reply
@Mark Hennings Thank you so much. By the way, it was not hard. :)
a = ⎝ ⎛ − 3 r sin θ 0 2 1 3 r cos θ ⎠ ⎞ b = ⎝ ⎛ 3 r sin θ 0 2 1 3 r cos θ ⎠ ⎞ c = ⎝ ⎛ 0 r − 2 1 3 r cos θ ⎠ ⎞ d = ⎝ ⎛ 0 − r − 2 1 3 r cos θ ⎠ ⎞ Thus a ˙ = ⎝ ⎛ − 3 r cos θ 0 − 2 1 3 r sin θ ⎠ ⎞ θ ˙ b ˙ = ⎝ ⎛ 3 r cos θ 0 − 2 1 3 r sin θ ⎠ ⎞ θ ˙ c ˙ = ⎝ ⎛ 0 0 2 1 3 r sin θ ⎠ ⎞ θ ˙ d ˙ = ⎝ ⎛ 0 0 2 1 3 r sin θ ⎠ ⎞ θ ˙ and so ∣ a ˙ ∣ 2 = ∣ b ˙ ∣ 2 = 4 3 r 2 ( sin 2 θ + 4 cos 2 θ ) θ ˙ 2 ∣ c ˙ ∣ 2 = ∣ d ˙ ∣ 2 = 4 3 r 2 sin 2 θ θ ˙ 2 so the kinetic energy of the system is T = 2 1 m ( ∣ a ˙ ∣ 2 + ∣ b ˙ ∣ 2 + ∣ c ˙ ∣ 2 + ∣ d ˙ ∣ 2 ) = m ( ∣ a ˙ ∣ 2 + ∣ c ˙ ∣ 2 ) = 4 3 m r 2 ( 2 sin 2 θ + 4 cos 2 θ ) θ ˙ 2 = 2 3 m r 2 ( 1 + cos 2 θ ) θ ˙ 2 Since most of the particles are held in relative place by the remaining strings, the only electrostatic bond that does work is the bond between A and B , we we have a potential energy V = 4 π ε 0 q 2 A B 1 = 4 π ε 0 q 2 2 r 3 sin θ 1 so conservation of energy tells us that 2 3 m r 2 ( 1 + cos 2 θ ) θ ˙ 2 + 4 π ε 0 q 2 2 r 3 sin θ 1 = 4 π ε 0 q 2 2 r 3 sin θ 0 1 where θ 0 = sin − 1 3 1 is the initial angle of the system, so r 2 θ ˙ 2 = 1 2 π ε 0 m r 3 q 2 1 + cos 2 θ 3 − csc θ Thus the system oscillates in the range θ 0 ≤ θ ≤ π − θ 0 , and we have ∣ a ˙ ∣ 2 = ∣ b ˙ ∣ 2 ∣ c ˙ ∣ 2 = ∣ d ˙ ∣ 2 = 1 6 π ε 0 m r 3 q 2 1 + cos 2 θ ( 3 − csc θ ) ( 1 + 3 cos 2 θ ) = π ε 0 m ℓ q 2 8 3 ( 1 + cos 2 θ ) ( 3 − csc θ ) ( 1 + 3 cos 2 θ ) = 1 6 π ε 0 m r 3 q 2 1 + cos 2 θ ( 3 − csc θ ) sin 2 θ = π ε 0 m ℓ q 2 8 3 ( 1 + cos 2 θ ) ( 3 − csc θ ) sin 2 θ If ξ is the maximum of 8 3 ( 1 + cos 2 θ ) ( 3 − csc θ ) ( 1 + 3 cos 2 θ ) over the range θ 0 ≤ θ ≤ π − θ 0 , then we see that the maximum speeds of A and B are V A = V B = π ε 0 m ℓ q 2 ξ while the maximum speeds of C and D are V C = V D = π ε 0 m ℓ q 2 8 3 3 − 1 , achieved when θ = 9 0 ∘ , and hence α = 2 ξ + 2 8 3 3 − 1 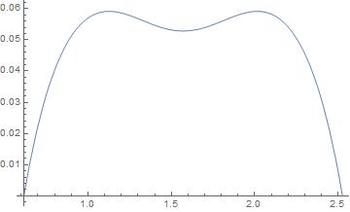 Numerical methods tell us that
ξ
=
0
.
0
5
9
1
2
7
9
(not achieved when
θ
=
9
0
∘
, but when
θ
=
6
4
.
5
6
1
5
∘
and
1
8
0
∘
−
6
4
.
5
6
1
5
∘
- the plot of
8
3
(
1
+
cos
2
θ
)
(
3
−
csc
θ
)
(
1
+
3
cos
2
θ
)
on the right measures the angle in radians, though), and hence
α
=
0
.
9
4
6
0
2
5
. Note that the maximum speeds of
A
and
B
are not attained when
θ
=
9
0
∘
, although the book from which this problem came claimed that it did.
Numerical methods tell us that
ξ
=
0
.
0
5
9
1
2
7
9
(not achieved when
θ
=
9
0
∘
, but when
θ
=
6
4
.
5
6
1
5
∘
and
1
8
0
∘
−
6
4
.
5
6
1
5
∘
- the plot of
8
3
(
1
+
cos
2
θ
)
(
3
−
csc
θ
)
(
1
+
3
cos
2
θ
)
on the right measures the angle in radians, though), and hence
α
=
0
.
9
4
6
0
2
5
. Note that the maximum speeds of
A
and
B
are not attained when
θ
=
9
0
∘
, although the book from which this problem came claimed that it did.