I.E Irodov Exercise 4.54
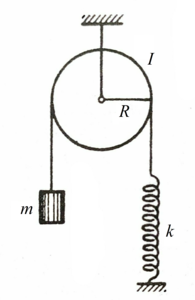 As shown in the figure, the radius of the pulley is
and its moment of inertia relative to the frictionless rotation axis is
. The mass of the body is
and the spring stiffness is
. The mass of the thread and the spring is negligible, the thread does not slide over the pulley.
As shown in the figure, the radius of the pulley is
and its moment of inertia relative to the frictionless rotation axis is
. The mass of the body is
and the spring stiffness is
. The mass of the thread and the spring is negligible, the thread does not slide over the pulley.
The angular frequency of small oscillation of the arrangement is given by
Find .
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
I will alter the nomenclature a bit. Let k be the spring constant, and let x be the spring displacement from equilibrium. The system Lagrangian has two kinetic energy terms (for the mass and the pulley), and two potential energy terms (for the mass and the spring).
L = 2 1 m x ˙ 2 + 2 1 I ( R x ˙ ) 2 + m g x − 2 1 k x 2 = 2 1 ( m + R 2 I ) x ˙ 2 + m g x − 2 1 k x 2
Equation of motion:
d t d ∂ x ˙ ∂ L = ∂ x ∂ L
Evaluating results in:
( m + R 2 I ) x ¨ = − k x + m g
The oscillation comes from the homogeneous equation, which is:
x ¨ = − m + R 2 I k x
This corresponds to simple harmonic motion with the following angular frequency. Note that this applies to all oscillations; not just small ones.
ω = m + R 2 I k