I.E Irodov Exercise 4.59
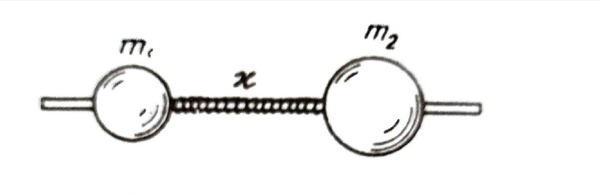
Two balls with masses m 1 and m 2 are slipped on a thin horizontal rod. The balls are interconnected by a light spring of stiffness x . The left hand ball is imparted the initial velocity v 1 .
If the oscillation frequency of the system in the process of motion is given by
( m 1 m 2 x ( m 1 + m 2 ) ) α
find α .
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Krishna Karthik Nice, interesting thanks. Upvoted
Log in to reply
No problem mate. Is the graph physically correct? I sure hope so. Fun problem btw. I want to see how Karan Chatrath or Steven Chase did it.
Log in to reply
I numerically integrated as well. I don't think the center of mass will oscillate. It should move with constant velocity, since the spring forces are internal to the system.
Log in to reply
@Steven Chase – @Steven Chase Yes I was also thinking that only. Therefore I decided not to say anything until real legends come.
@Steven Chase – So it moves to the right at a constant velocity? The centre of mass doesn't accelerate for the exact reason you said, despite the fact that the blocks shift to the right.
Log in to reply
@Krishna Karthik – Just take a mass-weighted average of the velocities of the two blocks, and you will see that it is constant
Log in to reply
@Steven Chase – Yeah. Thanks; I found the same result in a gravitating system with two bodies.
@Steven Chase – I found a video about this problem where the guy says at 2:30 that it will move to the right with both masses oscillating: https://www.youtube.com/watch?v=c1K1cYLTFOo
But yeah; the velocity of the centre of mass does remain the same.
Log in to reply
@Krishna Karthik – @Krishna Karthik WTF Who said you to see solution.?? Think yourself.
Log in to reply
@Talulah Riley – I saw the solution after I solved the problem.
@Steven Chase @Krishna Karthik Refresh my new latest problem
This particular problem can be solved just purely by dimensional analysis. For the dimensions of ω to be T − 1 , the value of α must be 0 . 5 . You can check this yourself. This question can be solved without any challenge.
But solving this rigorously can be done as follows:
Let the coordinate of m 1 be x 1 and that of m 2 be x 2 . Let the natural spring length be L o . Applying Newton's second law to each of the masses gives:
m 1 x ¨ 1 = x ( x 2 − x 1 − L o ) m 2 x ¨ 2 = − x ( x 2 − x 1 − L o )
Dividing the first equation by m 1 and the second one by m 2 and subtracting the 1st equation from the second equation gives:
x ¨ 2 − x ¨ 1 + x ( m 2 1 + m 1 1 ) ( x 2 − x 1 − L o ) = 0
Let: x 2 − x 1 − L o = y ⟹ y ¨ + ω 2 y = 0
ω 2 = m 1 m 2 x ( m 1 + m 2 )
Yeah. I solved it dimensionally too; but I also derived the correct expression for the frequency. But the fact that the frequency is a square root makes for a big hole in this problem. I think the "form" should be slightly altered. Nice solution.
I just used the classical analytical solution that many people used. However, here's something more interesting.
I programmed a time-domain simulation of the motion. The main idea is to use two cartesian coordinates and compute the distance between the two blocks at each timestep, and compute the direction and magnitude of the spring force. It's relatively simple as a simulation.
Basically, the force that the spring imparts on block 1 and 2 are:
s = ( x − y ) − l
Where x and y are the coordinates of block 1 and 2 respectively. In the simulation code, the centre of the spring is at the origin.
∣ F s ∣ = k ( x − y − l )
Hence:
F 1 = k ( x − y − l ) i ^
F 2 = − k ( x − y − l ) i ^
These are the two equations which will be solved numerically. Numerical integration does almost everything for you; it's crazy.
Here's a graph of the motion and the code:
It looks like the blocks oscillate back and forth, but ultimately the whole system moves to the right indefinitely, since there's no friction. I've been told that this is the realistic result assuming there's no friction.