IIT JEE 1982 Maths - MCQ Question 12
There exists a function f ( x ) satisfying: f ( 0 ) = 1 , f ’ ( 0 ) = − 1 , f ( x ) > 0 for all x and:
In case you are preparing for IIT JEE, you may want to try IIT JEE 1982 Mathematics Archives
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
[The problem has been edited and this comment is no longer relevant.]
That does not make any sense. f ′ ( x ) is a very local property.
It is possible for f ′ ′ ( x ) to be less than 0 for some x. As an explicit example,
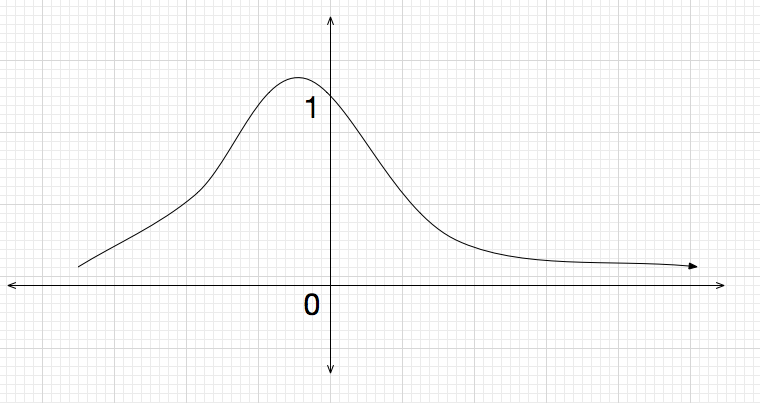
It is clear that f ′ ′ is not always greater than 0. In fact, f ′ ′ ( 0 ) < 0 .
Are you sure this is a JEE problem?
Log in to reply
It seems that you are not getting the question...
It is given that one of the options is true for all x. Then which option could that be? (Or which of the following option must that be?) (If you unserstand this, please help to rephrase the question - perhaps, rephrasing may not be necessary given that 6 out of 7 attempts chose the 'correct' option.)
Sure, f''(x) may not be positive for all x. But the quantifier 'for all' is not an option - the quantifier is already given!
As far as 'whether this question was really in JEE?', I am not sure. I have one reference book, in which I could not find this question, but I did found it here on Slide 14, Problem 12: IIT JEE Mathematics 1982
As far as my solution is concerned, I am ready to accept that it is wrong and delete it, if someone else too says that it is non-sense; or given that the question and answer is correct, a better (or 'correct') solution is found.
Log in to reply
My issue lies with "Which of the following must also be true, given that it is true for all real x?". My immediate reading of it is "If it is given that the option is true for all real x, then the option is (by definition) true and hence the answer has to be correct". I see that what is really wanted is instead
It is given that one of the options is true for all x.
Looking at the slide, I see that your question is not a direct copy of it entirely. The phrasing that you introduced has affected the problem. That's what I meant by "Are you sure this is a JEE problem", IE you don't have the exact duplicate (I'm assuming the slide show is accurate) of the phrasing that they used.
A much better way to phrase what you are trying to say is "For which of the following conditions, does there exist such a function, such that the condition holds true for all real x?". But, given how awkard the statement is, my preference is (for me) to update the choices instead. Let me know how you would like to proceed.
As to why people could solve the question, I believe most make an assumption that the question has a valid answer, or they ask themselves "What is the most reasonable interpretation I could take?". The jump in thinking invovled here, also explains why only 25% people attempted it (because it takes a lot of effort to understand what is truly being asked), and then that most get it right (once they understand what you actually meant). However, I work from what is actually stated, to ensure that others can easily interpret the problem.
Your solution is essentially correct. It did not make sense to me because of my above interpretation. To improve it, make sure you state what you exactly mean. For example, instead of "the derivative must increase" (supposedly referring to the point x = 0 ), what is actually true is "the derivative must eventaully increase". IE it is possible for the function to satisfy f ′ ( 1 ) < f ′ ( 0 ) , but not that f ′ ( a ) < f ′ ( b ) for all a > b .
Log in to reply
@Calvin Lin – You may change the options to what they are in the 'original' question, but that repeating 'for all' phrase is just a bit annoying... Editted the solution to add the word 'eventually'.
Log in to reply
@Shubhamkar Ayare – K, I've edited the options. Thanks.
Since f(x)>0 for all real x and f'(0)=-1<0, the derivative must eventually increase so that the graph avoids reaching y=0 line. Hence f''(x) must be positive.