I'm on my limit!
Shopsuey wants to buy some loaves of bread. When the baker asked him how many loaves he would take, Shopsuey gave him the following paper. How many loaves he took?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
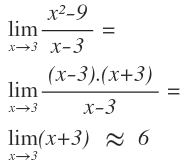
Why does the last line say lim x → 3 ≈ 6 ?
or we can use the L'Hospital Rule.
Log in to reply
Sure, but why should we make it more difficult?
Log in to reply
using L'hospital is more easier to me than factorizing something. Because in this rule we just have to differentiate and nothing else.
Log in to reply
@Trishit Chandra – Could you post a solution using the L'hospital Rule? Thank you.
Since the numerator and denominator both approach 0 , by L'Hôpital's rule, x → 3 lim x − 3 x 2 − 9 = x → 3 lim 2 x = 6 . While this may look neat, it takes more than twice as long to verify the limits are both 0 and then differentiate and evaluate, than it does to simply factor it, since it is of the form a 2 − b 2 .
In other words, it is faster to factor since minimal thought is required; ( x 2 − 9 ) can be factored in a split second if you know that 9 = 3 2 . If you use differentiation, though, it becomes a process of 3 separate evaluations, so even if you can differentiate super-fast, it still requires 2 more evaluations than the factoring method.