Imagine the world
There is a collection of points inside a unit cube that are closer to the center of the cube than to any of the cube’s vertices.
What is the volume of this 3D region?
 The true shape of the 3D region is
not
shown.
The true shape of the 3D region is
not
shown.
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Great explanation, thank you!
For me the description looks like that there is not enough info. With the info given you could also just have a very small volume in the center. Where am I wrong?
Log in to reply
The question meant to ask the volume of the region containing ALL the points closer to the center than to the vertices.
I'm with Lauritz, I cant get past the possibility that 8 points could form a cube any size inside the unit cube, for example.
Log in to reply
If you combine 8 of these cubes into a 2 × 2 × 2 cube, the centres of these cubes will themselves be the vertices of a 1 × 1 × 1 cube. If you repeat the cubes indefinitely, all the centres of the original cubes will themselves serve as the vertices of new cubes. Likewise, the vertices of the original cubes will be the centres of the new cubes. Those points that are nearest a vertex in the original lattice will be nearest a centre in the new lattice, and vice versa. What I've basically done is to show by symmetry that 2 1 of the volume is nearest a vertex, and 2 1 of the volume is nearest a centre.
In this problem, we must find the inter section of 8 spheres of unit radius which are drawn at 8 vertices of the unit cube in question. However, such a volume will be quite difficult to calculate.
This should have been placed under "Advanced" instead.
For each point in the cube, we need only consider the vertex V closest to it. Due to symmetry, the points nearest each of the 8 vertices comprise one eighth of the cube, more specifically a cube with a side 2 1 , one vertex of which is the center, with V on the opposite side of the cube. This means the problem is equivalent to finding the volume of the region of points closer to one vertex of a unit cube than the opposing one, which by symmetry is exactly 2 1 .
Nice interpretation via symmetry!
Is it also possible to find the surface area of this region?
Log in to reply
Sure - again, using the same deductions, we need to find the area of the region of points an equal distance from, say, 0 , 0 , 0 and 1 , 1 , 1 . There’s a number of ways to see this region is a plane, for instance if we consider the cube in a coordinate system, x 2 + y 2 + z 2 = ( 1 − x ) 2 + ( 1 − y ) 2 + ( 1 − z ) 2 ∴ x + y + z = 2 3 , which is an equation of a plane. From the equation it’s clear that the plane includes 6 of the midpoints of the cube’s edges, and so the cross section is a regular hexagon with side length 2 2 , making the area 4 3 3 .
I remember seeing this problem in an anime.
Log in to reply
You talking about assassination classroom right
Log in to reply
yes true its in assassination classroom..i think second-semester test scene but I don't think they solved it properly
Log in to reply
@Ju Lu – I think they did solve it properly, but they explained it terribly.
Log in to reply
@Zain Majumder – They were using spheres and stuff man.. that's wrong
Log in to reply
@Ju Lu – Oh yeah, they were trying show that the shape of the region did not affect the solution, except for the fact that it has reflectional symmetry. The whole time I remember thinking, "but the shape isn't a sphere!"
Awesome deduction!!
Beautiful!
I figured out the same solution as you. Yours is well-worded, btw.
If the cube has a volume of 1 then how can fully half be nearer the centre than a corner. There must be some part of the volume that is equidistant. So while there are equal amounts closer to the centre and closer to one of the vertices this cannot be half the volume for each. Can it?
Log in to reply
While there are, strictly speaking, points equidistant to the center and a corner, you can imagine they form a sort of hollow “shell”. Since this “shell” has a thickness of 0 and a finite area, it’s volume is naturally also 0 .
More rigorously, if we consider a 3D coordinate system, a point is equidistant to, say, 0 , 0 , 0 and 1 , 1 , 1 and contained within the unit cube precisely when x 2 + y 2 + z 2 = ( 1 − x ) 2 + ( 1 − y ) 2 + ( 1 − z ) 2 ≡ x + y + z = 2 3 . In this context, the volume of a region defined by a constraint is equivalent to the probability the constraint is satisfied, and the coordinates of a point x , y , z are U n i f ( 0 , 1 ) and since P ( x + y + z = 2 3 ) = ∫ 2 3 2 3 f ( c ) d c = 0 , where f ( c ) is the PDF of c = x + y + z , which, if interested, you can find easily via convolution of PDF’s, it’s once again clear the volume is 0 .
Relevant wiki: Volume - Problem Solving - Medium
The border of the mystery shape would consist of points that are exactly the same distance from the center of the cube to one of the edges. If the cube is lying flat on one of its faces, then the highest point of the border of the mystery shape would be directly above and centered over the cube at a distance x from the center of the cube and the same distance x away from all 4 top vertices of the cube. This point is the vertex of a right triangle made where one leg as half the diagonal of one of the faces of the cube ( 2 2 ), the other leg is the section above the center of the top face ( x − 2 1 ), and the hypotenuse is the distance between the point and the one of the 4 vertices of the cube ( x ).

By Pythagorean's Theorem, ( 2 2 ) 2 + ( x − 2 1 ) 2 = x 2 , which solves to x = 4 3 . By symmetry, there are 6 of these points by each face, all 4 3 away from the center of the cube, which can all be joined together to make an octahedron with sides of 4 3 2 . Since the mystery shape must be inside the cube, the octahedron is truncated.
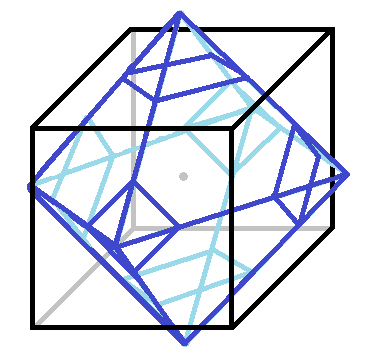
The volume of the truncated octahedron is the volume of the octahedron minus the 6 pyramids that are truncated. Since the volume equation of an octahedron with sides s is 3 2 s 3 , and s = 4 3 2 , the volume of the octahedron is 1 6 9 . Since the volume equation of a pyramid with a base area B and height h is 3 1 B h , and each pyramid has a height of h = 4 3 − 2 1 = 4 1 , with a base that is a square with diagonals that are 2 h = 2 ⋅ 4 1 = 2 1 , and so B = 8 1 ; the volume of each pyramid that will be truncated is 9 6 1 . Therefore, the volume of the truncated octahedron is 1 6 9 − 6 ⋅ 9 6 1 = 2 1 = 0 . 5 .
Great man!!
Excellent detailed solution. Bravo!
Wow, absolutely brilliant... 👏
Hey, why can't the mystery shape be a sphere having centre at the centre of the cube and radius equal to the distance between center and one of the faces.
Log in to reply
The sphere you described would have points on its surface that is also at the center of each face. Each of these points would be 2 1 units away from the center of the unit cube, but 2 2 units away from the four vertices of the face. Since these are different lengths these points cannot be on the surface of the mystery shape.
The problem isn't worded well. I think they meant to ask for the ~largest~ set of points, which they didn't. This seems to happen on this site. Which is somewhat less than...brilliant.
Nice solution. But I did not understand the first line. If we want to have a collection of points that are closer to the centre than the vertices, then why would the boundary points of that region will have the same distance from the centre and the corresponding vertex ?
Log in to reply
When the boundary points are defined as having the same distance from the center and a vertex, anything inside the boundary points would have to be closer to the center, and anything outside the boundary points would be further from the center. Therefore, the desired collection of points (ones that are closer to the center than the vertices) is contained in the boundary points.
I want to thank you for the effort you have taken to explain us your solution in such a simplistic manner.
Why is only one answer correct, when it just says "volume of the collection of points" and not "biggest possible Volume that a collection of points can have under named conditions"?
Log in to reply
It's a collection of points that meet certain requirements (that they are closer to the center of the cube than to any of the cube’s vertices) and those requirements only make one shape and therefore only one possible volume.
Log in to reply
a small cube inside the shape would also meet the requirements...
Log in to reply
@Lenny Post – No, it must be a truncated octahedron, not a small cube. See my solution above.
Divide the cube into 8 smaller cubes.
Each small cube has one of the original cube vertices and the center of the original cube.
Half of the points in every small cube is closer to the center due to symmetry, so the volume that contains all points that closer to the center is half the volume of the unit cube. V= 0.5
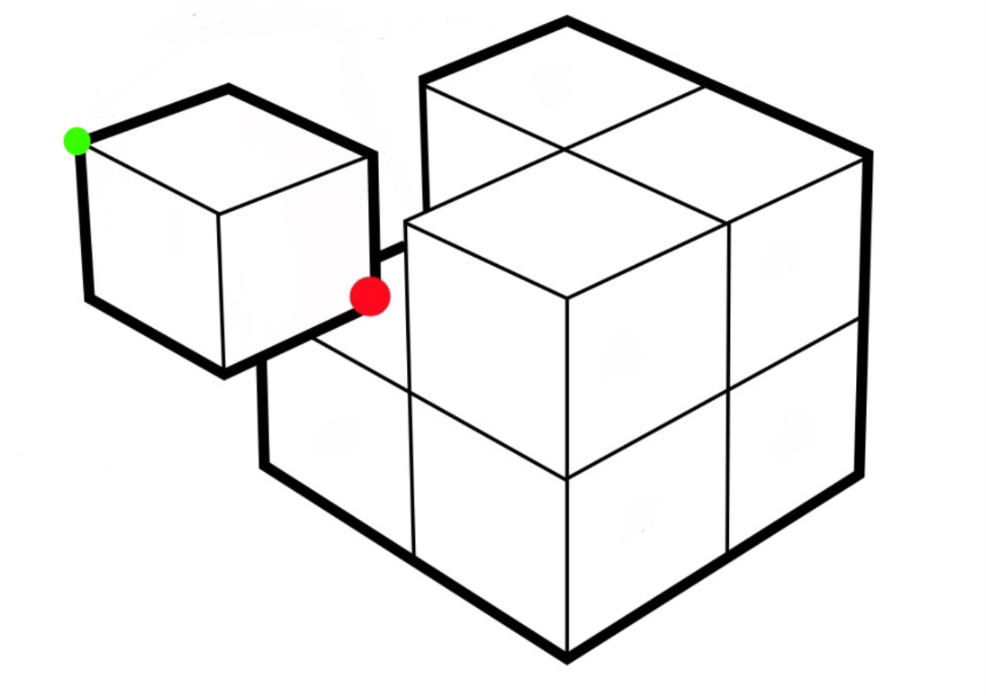
This is by far the most intuitive and easy-to-understand explanation.
It is indeed!
I got the general idea of how the shape of the border figure is but I have no idea how to calculate it. And the other explanations were too complicated for me to understand.
But this one here is amazing!
Thumbs up to Stewart Gorden: Like others I took 1/8 of the cube with a corner centered on the origin. Thus the farthest corner is at (1/2,1/2,1/2). I took a generic point at (x,y,z). The distance from this point to the center is d c 2 = x 2 + y 2 + z 2 . The distance to the nearest vertex is d v 2 = ( 1 / 2 − x ) 2 + ( 1 / 2 − x ) 2 + ( 1 / 2 − z ) 2 . Now d c 2 ≤ d v 2 so d c 2 − d v 2 ≤ 0 . With a little bit of algebra we can show that x + y + z ≤ 3 / 4 . This is the equation of a plane that slices through the cube separating the two regions. I guess one could triple integrate, but I am too rusty at the moment. Instead I calculated the volume of the pyramid that is defined by the three points (3/4,0,0), (0,3/4,0), and (0,0,3/4): V P = 9 / 1 2 8 , then subtracted the three little pyramids that stick out past the limits of the cube. These all have 1/3 the linear dimensions of V P , but there are three of them so subtract off V p = 1 / 1 2 8 . So the volume in one octant is V = 8 / 1 2 8 . Since there are 8 octants the sought after volume is 64/128 = 1/2.
I included a 3d view of the plane and cube below. The full shape is some sort of polyhedron. My picture indicates four facets after trimming, but I think the other octants would match up with the trimmed faces. So 8(1+3) is counting some twice, therefore I think there are 8+8*3/2 = 20 faces. I now believe 20 is wrong. I think 4 of the faces formed by trimming match up to form a square. Thus there are 8 + 24/4 = 14 faces. This would be a truncated octohedron.


I made a series of shapes in this family on my school's 3d printer. The octahedron, the cube with octahedron removed, and the truncated octahedron. I never thought to find the volume of the cube with octahedron removed, but you can bet my geometry students will get a crack at it.
Without figuring out the shape of the 3D region we're talking about, we can easily answer the question: Cut the cube into 8 smaller cubes with each side half the length of the original side. Consider any one of these little cubes. One vertex (call it A) is the original cube's center, and the opposite vertex (call it B) is a vertex of the big cube. So the question for this little cube is, what is the volume of points closer to A than B? There's no difference between A and B, in this regard; so the answer must be half of the little cube's volume. The same is true for all 8 little cubes, so the total volume of points closer to the center than the nearest vertex must be half the total volume.
Hmm. I see my solution is essentially the same as Ivo Zerkov's, which was published about a week earlier.
Intuition is insufficient to prove the answer, but it can help.
In 1D, a “unit cube” is a line segment (say from 0 to 1) of length 1. The set of points that are (closer to the segment’s midpoint than the endpoints)OR(equidistant to the midpoint and the closest endpoint), is the line segment from 0.25 to 0.75, of length 1/2.
In 2D, a “unit cube” is a unit square (side length 1). The set of points that are (closer to the center of the square than to the vertices)OR(equidistant to the center and the closest vertex) is a square inscribed in the unit square whose vertices are at the midpoints of the sides of the unit square. The diagonal of this new square is equal to the side length of the unit square, 1, so the side length of the new square is 1/sqrt(2) and the area of the new square is thus 1/2.
Though the above cases do not prove anything about the cases in higher dimensions, they do strongly suggest that the set of points that are (closer to the center of the unit cube)OR(equidistant to the center and the closest vertex) is a polyhedron with volume 1/2.
Divide the cube, through the planes of symmetry, into 8 smaller cubes.
Looking at each smaller cube, the vertex of the larger cube and the center of the larger cube will be opposing vertices in this smaller one.
The volume of the points nearer to each of them will be the same (1/2 of the smaller cube). Since the 8 cubes are the equal and they make up the larger one, the total volume of the points nearer to the center of the larger cube will also be 1/2.
This problem is actually simpler than it looks. Consider the cubes as repeating indefinitely in all directions. The vertices of the cubes form a simple cubic lattice, as do the centres of the cubes. You can interchange centres and vertices, and it will be the same. As such, the proportion of the volume that's nearer a centre than a vertex must be the same as vice versa.