Imbalanced Shapes!

Algebra Level 1

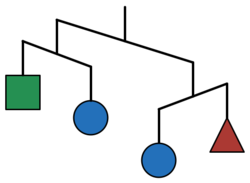
The diagram shows how a mobile will be balanced when left to hang.

What are the relative weights of these shapes?

Triangle > Rectangle > Circle Circle > Rectangle > Triangle Rectangle > Triangle > Circle Circle > Triangle > Rectangle Rectangle > Circle > Triangle Triangle > Circle > Rectangle

7 solutions

Chew-Seong Cheong
Apr 16, 2015

$\triangle + {\LARGE \circ} > \square + { \LARGE \circ} \quad \Rightarrow \triangle > \square$

The right arm: ${\LARGE \circ} > \triangle$

Therefore, ${\LARGE \circ} > \triangle > \square$

What logic???

Mohammad Moeen - 5 years, 7 months ago

$\triangle + {\LARGE \circ} > \square + { \LARGE \circ}$ means $\triangle + {\LARGE \circ}$ heavier than $\square + { \LARGE \circ}$

Chew-Seong Cheong - 5 years, 7 months ago

easy but taking mind stress

Ashutosh Verma - 6 years, 1 month ago

I lost these points: I believe the weights must be equal (at least in the case of an "ideal" mobile, with weightless rods). If one object were heavier, it would move all the way down, making the corresponding rod vertical.

Otto Bretscher - 6 years, 1 month ago

No sir. Imagine pulling a rope from the top of a boat mast as hard as you can sideways... the boat will be tilted not perfectly vertical. You are lighter than the boats keel. But you can tilt it a littlebit... only when you release the rope will the boat once again be plumb.

Caspar Cash - 6 years, 1 month ago

In the case of the boat we have the torque of the buoyancy, with no analogous effect in the case of the (ideal) mobile. The question is simple: If you have different weights and a slightly tilded top rod, are you saying the torque is zero? Obviously, we need that to have an equilibrium.

Otto Bretscher - 6 years, 1 month ago

Nope. If you calculate the center of gravity, you can place the fulcrum so that both weights are evenly balanced. I prefer to use moment calculations.

Rob McNearny - 5 years, 3 months ago

My objection is valid...think about it! (They don't do this kind of nonsensical problems anymore)

If the blue circle is heavier than the red triangle, for example, than the blue circle will move "all the way down", making the bar on top vertical... that is just Physics 101.

Otto Bretscher - 5 years, 3 months ago

Yes, of course. But for the ease of writing the problem. We should assume that these are discrete balances which don't react to precise values of the weights on two arms but rather just tilt when there is a difference.

Chew-Seong Cheong - 6 years, 1 month ago

My point is: The bars tilt all the way down when there is a difference in weight. The torque doesn't go away just because we tilt the bar a little as shown in the figure. Flawed physics!

Otto Bretscher - 6 years, 1 month ago

@Otto Bretscher – I know the Physics does not make sense. But this is an algebraic problem not a Physics one. The balances are purely ">" and "<".

Chew-Seong Cheong - 6 years, 1 month ago

@Chew-Seong Cheong – One should not use false physics to illustrate math ;) The notions of torque and equilibrium are important, and this kind of nonsensical stuff certainly sends the wrong message.

Otto Bretscher - 6 years, 1 month ago

@Otto Bretscher – Yes Sir, the diagram is really confusing ! Due to which there is difficulty understanding the problem

Anirban Mandal - 5 years, 7 months ago

@Anirban Mandal – I think there are no more of this type of problems.

Chew-Seong Cheong - 5 years, 7 months ago

I got the right answer using this too... but according to the picture, the difference in weight between the circle and triangle should be greater than the difference in weight between the circle and rectangle... it's mind-boggling! But logic always wins so I somehow got this right.

Chris White - 5 years, 7 months ago

Luis Dato
Apr 20, 2015

Given the choices, the circles weigh the same. So if the scale only had both circles at each side it would not move to one side. Clearly the weight of the triangle added to the weight of the circle is greater than the weight of the circle and the square, which is why the triangle is the second heaviest shape, making the square the lightest.

It still bothers me that the choices say rectangle.

All right-angled quadrilaterals are rectangles unless declared that the four sides are equal to be called a square.

Yves Tedera - 6 years, 1 month ago

Thanks! :)

Luis Dato - 6 years, 1 month ago

Scott Ripperda
Dec 7, 2015

This problem messed with my head a bit, before I realized that right side is at a lower height. Cool problem!

Breckin Hockings
Jul 17, 2019

Circle is lowest in both therefore heaviest, than the triangle, than the square

Achille 'Gilles'
Feb 18, 2016

On the small bars, the circles are heavier on both side so circle is the heaviest. On the long bar, triangle+circle is heavier that square+circle hence triangle is heavier than square.

So in order

➚ Circle is the heaviest

➙ Triangle is in the middle

➘ Square is the lightiest

Yves Tedera
Apr 22, 2015

Let c=circle, t=triangle, r=rectangle

C, as shown, has been the heaviest since it sank into the bottom as compared to t and r.

However, c+t is shown to be heavier than c+r.

c+t > c+r

t > r

Therefore the arrangement is c>t>r

Henrique Ribeiro
Apr 20, 2015

I thought this way: the circles are the lowest, so, they can be the heaviest pieces of both system (square + circle and circle + triangle). In order, triangle is heavier than square by the same logic.

Imbalanced Shapes!

7 solutions

0 pending reports