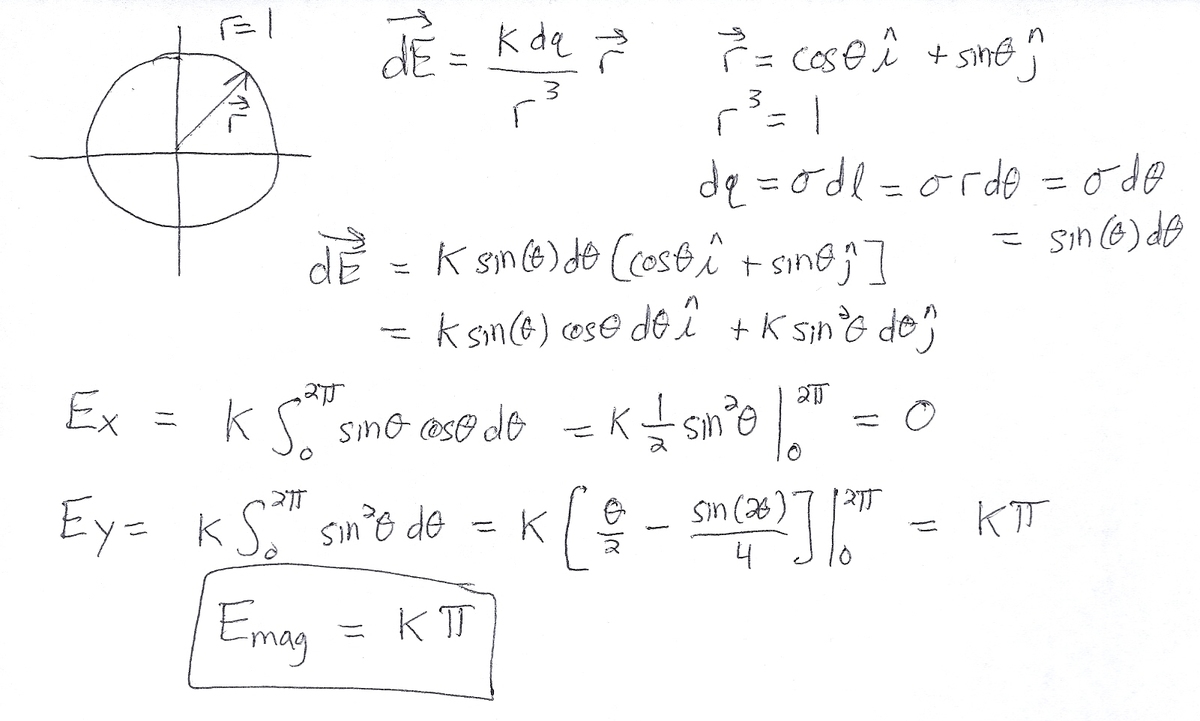Imperfect Symmetry

Charge is unevenly distributed over a unit circle centered on the origin $(0,0)$ . The linear charge density is $\sigma=\sin(\theta)$ .

The magnitude of the electric field at the origin can be expressed as $\alpha$ $k$ , where $k$ is the Coulomb constant. Enter the value of $\alpha$ , given to two decimal places.

Details and Assumptions:

Assume standard SI units for all quantities.

Note that $\sin(\theta)$ is negative for some values of $\theta$ .