Shocked Face

If $r$ is the radius we seek, then $AB = 1; BC = 2, AD = r+2; BD = 3-r; CD = r+1$

Stewart's theorem gives $3 \times 2 \times 1 + (3-r)^2 \times 3 = (r+1)^2 \times 1+ (r+2)^2 \times 2$ $6 + 27 -18r = 2r + 1 + 8r + 8$ $24 = 28r$ giving $r = \frac{6}{7}$ .

Let $A$ be the center of the circle $x^{2} + y^{2} = 4$ , $B$ be the center of the circle $x^{2} + (y - 1)^{2} = 9$ , $C$ be the center of the circle $x^{2} + (y - 3)^{2} = 1$ and $D$ be the center of the sought after inscribed circle. Also, let $r$ be the radius of the circle with center $D.$ Then, using the Cosine rule on $\Delta ACD$ we have that

$|AD|^{2} = |AC|^{2} + |CD|^{2} - 2*|AC|*|CD|*\cos(\angle ACD)$

$\Longrightarrow (2 + r)^{2} = 9 + (1 + r)^{2} - 6(1 + r)\cos(\angle ACD)$

$\Longrightarrow \cos(\angle ACD) = \dfrac{3 - r}{3(1 + r)}.$

Next, using the Cosine rule on $\Delta BCD$ and noting that $\angle BCD = \angle ACD$ , we have that

$|BD|^{2} = |BC|^{2} + |CD|^{2} - 2*|BC|*|CD|*\cos(\angle ACD)$

$\Longrightarrow (3 - r)^{2} = 4 + (1 + r)^{2} - 4(1 + r)\cos(\angle ACD)$

$\Longrightarrow \cos(\angle ACD) = \dfrac{2r - 1}{1 + r}.$

Equating the two expressions for $\cos(\angle ACD)$ gives us

$\dfrac{3 - r}{3(1 + r)} = \dfrac{2r - 1}{1 + r} \Longrightarrow 3 - r = 6r - 3 \Longrightarrow 7r = 6 \Longrightarrow r = \dfrac{6}{7}.$

Thus $a + b = 6 + 7 = \boxed{13}.$

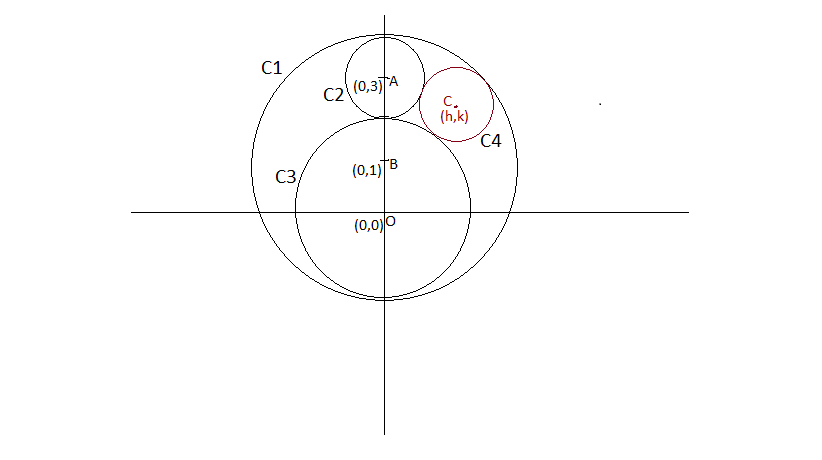
Let $r$ be the radius of circle C4.

C4 touches C1 internally, $\Rightarrow \quad 3-r=\sqrt { { h }^{ 2 }+{ (k-1) }^{ 2 } } \\ \Rightarrow \quad { r }^{ 2 }-6r+2k+8={ h }^{ 2 }+{ k }^{ 2 }\longrightarrow \boxed { 1 }$

C4 touches C2 externally, $\Rightarrow \quad 1+r=\sqrt { { h }^{ 2 }+{ (k-3) }^{ 2 } } \\ \Rightarrow \quad { r }^{ 2 }+2r+6k-8={ h }^{ 2 }+{ k }^{ 2 }\longrightarrow \boxed { 2 }$

C4 touches C3 externally, $\Rightarrow \quad 2+r=\sqrt { { h }^{ 2 }+{ k }^{ 2 } } \\ \Rightarrow \quad { r }^{ 2 }+4r+4={ h }^{ 2 }+{ k }^{ 2 }\longrightarrow \boxed { 3 }$

Solving equations 1. 2 and 3, we get $r=\frac { 6 }{ 7 }$ ,

Hence, answer is $6+7=\boxed { 13 } .$

Using Descartes circle theorem . Let $r \neq 0$ be the radius we are seeking, then $2(\frac{1}{4} + \frac{1}{9} + 1 + \frac{1}{r^2}) = (\frac{1}{2} + 1 - \frac{1}{3} + \frac{1}{r})^2 \iff (\frac{1}{r} - \frac{7}{6})^2 = 0 \iff \boxed{r = \frac{6}{7}}.$ Or in otrher words,

Proposition.- Let $\mathbb{R}$ be the set of real numbers, then are equivalents:

a) $r = \frac{6}{7}$

b) $\frac{1}{r} = \frac{7}{6}$

c) $(\frac{1}{r} - \frac{7}{6})^2 = 0$

d) $2(\frac{1}{4} + \frac{1}{9} + 1 + \frac{1}{r^2}) = (\frac{1}{2} + 1 - \frac{1}{3} + \frac{1}{r})^2$

Proof.-

$a) \iff b)$ Trivial.

$b) \Rightarrow c)$ If $\frac{1}{r} = \frac{7}{6} \Rightarrow \frac{1}{r} - \frac{7}{6} = 0 \Rightarrow (\frac{1}{r} - \frac{7}{6})^2 = 0$

$c) \Rightarrow b)$ If $(\frac{1}{r} - \frac{7}{6})^2 = 0 \Rightarrow (\frac{1}{r} - \frac{7}{6}) \cdot (\frac{1}{r} - \frac{7}{6}) = 0 \Rightarrow \frac{1}{r} = \frac{7}{6}$ .

Hence, so far, we have already proved $a) \iff b) \iff c)$ . Now

$a) \Rightarrow d)$ Trivial (calculation)

$d) \Rightarrow c)$ If $2(\frac{1}{4} + \frac{1}{9} + 1 + \frac{1}{r^2}) = (\frac{1}{2} + 1 - \frac{1}{3} + \frac{1}{r})^2 \Rightarrow \frac{49}{18} + 2\frac{1}{r^2} = (\frac{7}{6} + \frac{1}{r})^2 \Rightarrow \frac{1}{r^2} - \frac{2\cdot 7}{6r} + \frac{49}{36} = (\frac{1}{r} - \frac{7}{6})^2 = 0$

q.e.d