Incident Radiation
In the x y z -coordinate system, a thin solid disk of radius R lies in the x y -plane with its center at the origin. An isotropic light source is positioned at ( x , y , z ) = ( R , 0 , R ) .
What percentage of the light energy is incident on the disk (to one decimal place)?
The answer is 8.9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
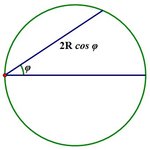 We need to determine the solid angle subtended by the disk from the light source. Setting up a system of spherical polar coordinates with the light source as the origin and the polar axis in the negative
z
-direction, we see that the ray of light emitted by the source in a direction determined by polar angles
θ
,
ϕ
will only hit the disk if it strikes a chord of length
2
R
cos
ϕ
, for
−
2
1
π
≤
ϕ
≤
2
1
π
. Thus the ray of light will strike the disk provided that
tan
θ
≤
2
cos
ϕ
−
2
1
π
≤
ϕ
≤
2
1
π
Thus the solid angle subtended by the disk is
Ω
=
∫
−
2
1
π
2
1
π
d
ϕ
∫
0
tan
−
1
(
2
cos
ϕ
)
sin
θ
d
θ
=
∫
−
2
1
π
2
1
π
d
ϕ
[
−
cos
θ
]
θ
=
0
tan
−
1
(
2
cos
ϕ
)
=
∫
−
2
1
π
2
1
π
(
1
−
1
+
4
cos
2
ϕ
1
)
d
ϕ
=
π
−
2
∫
0
2
1
π
5
−
4
sin
2
ϕ
d
ϕ
=
π
−
5
2
K
(
5
4
)
using the complete elliptic integral
K
of the first kind. Thus the percentage of emitted light that strikes the disk is
1
0
0
×
4
π
Ω
=
2
5
−
π
1
0
5
K
(
5
4
)
≈
8
.
9
3
4
0
6
%
We need to determine the solid angle subtended by the disk from the light source. Setting up a system of spherical polar coordinates with the light source as the origin and the polar axis in the negative
z
-direction, we see that the ray of light emitted by the source in a direction determined by polar angles
θ
,
ϕ
will only hit the disk if it strikes a chord of length
2
R
cos
ϕ
, for
−
2
1
π
≤
ϕ
≤
2
1
π
. Thus the ray of light will strike the disk provided that
tan
θ
≤
2
cos
ϕ
−
2
1
π
≤
ϕ
≤
2
1
π
Thus the solid angle subtended by the disk is
Ω
=
∫
−
2
1
π
2
1
π
d
ϕ
∫
0
tan
−
1
(
2
cos
ϕ
)
sin
θ
d
θ
=
∫
−
2
1
π
2
1
π
d
ϕ
[
−
cos
θ
]
θ
=
0
tan
−
1
(
2
cos
ϕ
)
=
∫
−
2
1
π
2
1
π
(
1
−
1
+
4
cos
2
ϕ
1
)
d
ϕ
=
π
−
2
∫
0
2
1
π
5
−
4
sin
2
ϕ
d
ϕ
=
π
−
5
2
K
(
5
4
)
using the complete elliptic integral
K
of the first kind. Thus the percentage of emitted light that strikes the disk is
1
0
0
×
4
π
Ω
=
2
5
−
π
1
0
5
K
(
5
4
)
≈
8
.
9
3
4
0
6
%
I took strips as my differential element with its ends at +/- θ and then integrated the solid angle and did the same as you did . I have checked my answer several times its coming 17.9 ie double of yours . I integrated from 0 to pi.
Log in to reply
Without details it is hard to comment. Did you divide by 2 π instead of 4 π ?
Log in to reply
I have not done that for sure. Thanks for your response I know its very crazy to ask the mistake without showing solution. It is difficult to present it and also at that time I was very furious of doing this question wrong by factor of 2. I will figure it out myself some time later or so. Thanks.
The most familiar scenario is that of an isotropic radiator (like a star) with an imaginary spherical shell surrounding it, through which the energy passes. If the radius of the shell is d , the power density is the total radiant power divided by the surface area.
P d = 4 π d 2 P t o t a l
For the sphere, we can simply integrate the scalar power density over the imaginary surface to calculate the total power, since the surface normal is everywhere parallel to the radiation flux. However, for arbitrary surfaces, this nice relationship does not hold.
For example, suppose there was an isotropic radiator in the middle of a right circular cylinder. In this case, integrating the simple scalar power density expression over the surface gives an absorbed power greater than that of the source. To fix this, we must introduce an additional term, which is the magnitude of the dot product between the unit flux directional vector and the unit surface normal. The differential absorbed power is:
d P a b s = P d d A ∣ n ^ ⋅ d ^ ∣
where P d is the scalar power density, d A is the differential surface area, n ^ is the unit surface normal vector, and d ^ is the unit displacement vector from the source to the surface. This is very similar to the solid angle calculation.
For this problem, begin by defining coordinates for the source:
( S x , S y , S z ) = ( R , 0 , R )
Use polar coordinates to define the coordinates of a point on the disk (notice that r and R are different):
( x , y , z ) = ( r c o s θ , r s i n θ , 0 )
Differential disk area:
d A = r d r d θ
Displacement vector:
d = ( r c o s θ − S x , r s i n θ − S y , 0 − S z ) = ( Δ x , Δ y , Δ z )
Unit displacement vector:
d ^ = ( Δ x ) 2 + ( Δ y ) 2 + ( Δ z ) 2 d
Unit surface normal ( k ^ is a unit-vector in the z-direction):
n ^ = k ^
Scalar power density:
P d = 4 π ∣ d ∣ 2 P t o t a l
Differential absorbed / incident power:
d P a b s = P d d A ∣ n ^ ⋅ d ^ ∣
Putting all of these elements together in a double integral and solving numerically yields the result that approximately 8 . 9 % of the total radiated power / energy is incident on the disk.
P a b s = ∫ 0 2 π ∫ 0 R d P a b s = ∫ 0 2 π ∫ 0 R P d d A ∣ n ^ ⋅ d ^ ∣
My Solution: Let light source places at origin (0,0,0), and the disk is at z=R position and polar function r = 2 R c o s θ , The percentage of Energy collide on disk is E 0 E = P = ∫ 4 π s 2 d A Which s = r 2 + z 2 = r 2 + R 2 , present the length from origin.
P = ∫ 4 π ( r 2 + R 2 ) r d r d θ = ∫ − 2 π 2 π ∫ 0 2 R c o s θ 4 π ( r 2 + R 2 ) r d r d θ = 8 π 1 ∫ − 2 π 2 π l n ( 4 c o s 2 θ + 1 ) d θ
Log in to reply
What numerical result do you get?
Log in to reply
I use Wolfram Alpha to get numerical result 0.120302956264900861874439... Can you please check where my solution has mistake?
Log in to reply
@Kelvin Hong – I think your integral is the same as mine, but with the dot product term always equal to 1. When I rerun mine and force the dot product to a constant 1, I get your result.
Log in to reply
@Steven Chase – Oh, I assume that all of the light are perpendicular beam on the disk but actually the light will shot at a acute angle. I forget to think about this incline angle. Thank you to let me know my mistake!
I use ∫ 4 π s 2 d A to express percentage of energy because it is fraction of integrated of area which collided the disk by the whole surface area 4 π s 2 .