Two Parent Circles and Their Baby Circle

Two circles with center A (That's Aareyan) and B (I don't know someone with B) having radius 6 and 216 respectively. If both of the circle are tangent to the line as shown in the figure find the radius of the maximum circle that is tangent to both circle and and the line with center O up to 4 decimal places.
The answer is 4.4081.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I learnt about this formula last year and that is why I was able to solve the question so fast. :)
Log in to reply
Can you tell me how one can obtain that formula ?
Log in to reply
There is a derivation here ... basically the same thing that @Shaun Leong is doing, but without the pretty figure
It can also be solved using Descartes' Theorem.
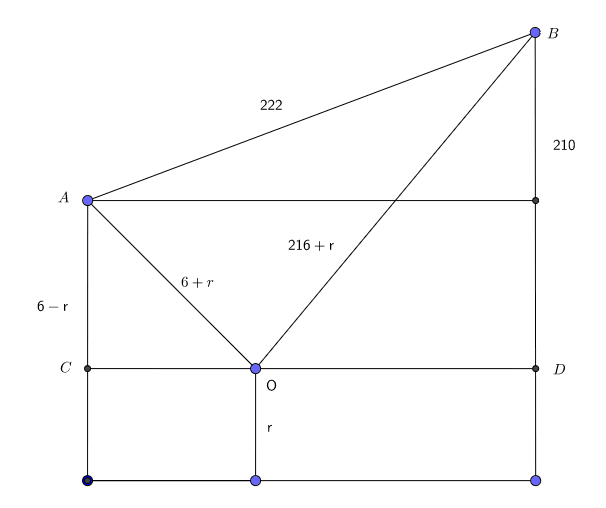
Image from GeoGebra .
Consider the above diagram which only considers the important points, namely the centres.
Let r be the radius of the circle.
Let C and D be the intersections of the line y = r with the radii from A and B to the horizontal line.
By Pythagoras' Theorem, C D = 2 2 2 2 − 2 1 0 2 = 7 2 C O = ( 6 + r ) 2 − ( 6 − r ) 2 = 2 6 r O D = ( 2 1 6 + r ) 2 − ( 2 1 6 − r ) 2 = 1 2 6 r
We have C O + O D = C D 2 6 r + 1 2 6 r = 7 2 r = 1 4 6 7 2 r = 4 9 2 1 6 ≈ 4 . 4 0 8 1
Log in to reply
Well yes! That is essentially my diagram except the lines by the side are vertical and I excluded the other regions, since we want to focus on the trapezium to compute the radius. (it is most certainly not drawn to scale)
A salute to our maths sir!This problem is dedicated to him.After all,he is too intelligent.I solved it btw,it was easy .
Log in to reply
I solved it too. Looks like my geometry isnt bad after all.
I did the same way but made some mistake!!
Same way.! Fine explanation
Since all other solutions are taken, I will use Descarte's Circle Theorem which states for four mutually tangent circles of radii
r
1
,
r
2
,
r
3
,
r
4
, the identity holds
(
r
1
1
+
r
2
1
+
r
3
1
+
r
4
1
)
2
=
2
(
r
1
2
1
+
r
2
2
1
+
r
3
2
1
+
r
4
2
1
)
We will call the desired radii x . Thus, we have four mutually tangent circles with radii x , 6 , 2 1 6 , ∞ . Substituting these values in we have ( x 1 + 6 1 + 2 1 6 1 ) 2 = 2 ( x 2 1 + 3 6 1 + 2 1 6 2 1 )
which is easy to solve.
Can you elaborate descrate's theorem with a diagram.
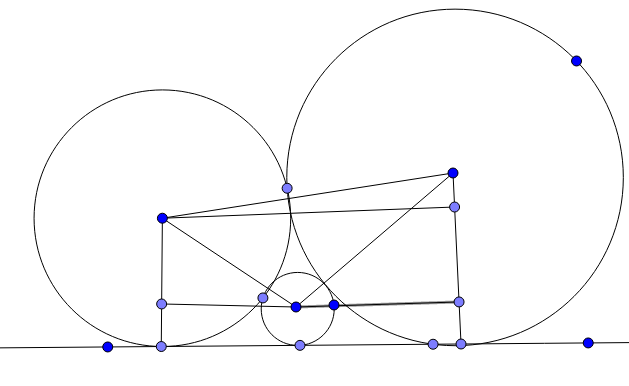
Using the well-known formula r 3 1 = r 1 1 + r 2 1 , where r 3 is the radius of the smallest circle, we find r 3 = ( r 1 + r 2 ) 2 r 1 r 2 = 4 9 2 1 6 ≈ 4 . 4 0 8 1 .