Inductor and Capacitance (07-09-2020)
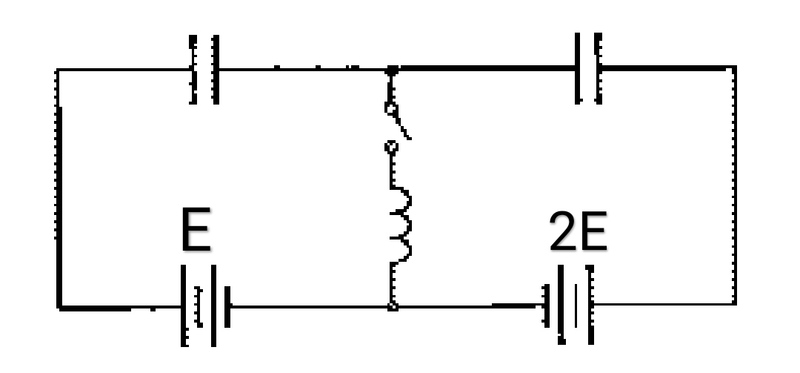
A circuit shown consists of two identical capacitors each of capacitance C , a coil of inductance L , two ideal batteries of electromotive force E and 2 E and a switch. The switch is open for a long time. The maximum current through the coil after the switch is closed is given by:
I m a x = α E L C
Find α .
The problem is taken from physics book pathfinder.
The answer is 2.121.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
@Steven Chase
please help me in this problem
Your matrix isn't rendering correctly for some reason. Great solution overall.
Log in to reply
@Krishna Karthik
Bro see my solution below. I just solved it in 4 steps .
But he is not bothered to say me atleast welldone.
Log in to reply
Who cares about them upvoting? I upvoted.
Log in to reply
@Krishna Karthik – @Krishna Karthik who cares ? meaning?
Log in to reply
@Talulah Riley – I mean why would you care so much if they see your solution or not?
Log in to reply
@Krishna Karthik
–
@Krishna Karthik yeah, that good, I don't care.
But the main thing is just compare my solution with him or Karan sir.
My solution is so much easy that even a 5year old guy can understand.
And regarding their solution even a 15 year old guy can commit suicide.
Log in to reply
@Talulah Riley – That's true. But that's the rigourous way of doing things. You should know that there are different ways of doing things.
Generally, for circuit problems like this, formulating differential equations is the proper way. Karan Chatrath used the Laplace Transform (a powerful tool) to solve the resulting differential equation.
You, however, solved it like a student doing a test would . You solved it the simple way. Note that time-domain simulations actually help you understand what's going on as well as the answer.
Your solution only finds the answer, not what's going on.
Test vs real life.
Knowing both is important.
Log in to reply
@Krishna Karthik
–
@Krishna Karthik i have used the concepts of Energy.
And I think everyone knows using the concepts of energy makes the problem easier.
If they do this in a test, Time of test will get over. all answer sheets will be collected by the invigilator (except your) in the examination Hall.
Examination centre will be closed.
Still their calculations are going. Ha ha :)
But in real life,their methods are really sexy.
Log in to reply
@Talulah Riley – Precisely. You have done it as a true test-taker would have. Nicely done.
There is a difference between finding out what's going on and finding the answer to a problem in physics.
Their method finds out what's going on, yours simply finds the answer. For that, I appreciate yours. For that, I appreciate theirs.
Each to their own :)
@Krishna Karthik
but overall their solutions are also good. I like to solve by different different method.
So every method is appreciated, whether it is big or small.
Log in to reply
I agree. Their solutions address not only the entire problem, but also the answer to the problem.
As a physicist however, you should know both ways of solving problems. However, almost always, formulating a differential equation and solving always trumps the latter .
But on a test, I would use your method because it's simple. For that, I like it.
Have you read any textbooks about solving differential equations? You should read almost as much as you solve problems. I find that you sometimes get too caught up in solving and practice.
Log in to reply
@Krishna Karthik i didn't understand the last line , which you want to say.
Log in to reply
I want to say that you solve a lot of problems. But I just want to know; do you read just as much? You are a great physicist indeed, because of years of practice.
I want to know: do you read, watch lectures, learn passively as well?
Log in to reply
@Krishna Karthik – @Krishna Karthik what is the meaning of . ““I find that you sometimes get too caught up in solving and practice.”
Log in to reply
@Talulah Riley – I mean I find that you solve a lot of problems. Practice is very good, but it is also good to learn passively. You are a very smart guy, which is why I think you like to solve problems.
I think reading and learning is just as important.
How come your brain doesn't get tired because of solving problems repeatedly? Sometimes I like to just take the back seat, and think.
Log in to reply
@Krishna Karthik
–
@Krishna Karthik
i read, but doesn't a lot.
As I am JEE student ,
Log in to reply
@Talulah Riley – You should read more about physics; about concepts, as much as problems.
Concepts and philosophical things should take your fancy. Sometimes I just like to watch professors or videos of 3Blue1Brown to relax and unwind.
@Krishna Karthik
Today I have a date with my girlfriend, so don't disturb me.
I will talk to you tomorrow. Bye :)
Log in to reply
Log in to reply
@Krishna Karthik
yes bro, I like to have a girlfriend.
This is my last reply on Brilliant today.
I will talk to you tomorrow, bye :)
I was trying to solve using the concepts of energy and finally it worked
When the switch is open,Energy residing in the capacitors
E
i
n
i
t
i
a
l
=
2
1
C
(
2
E
)
2
+
2
1
C
(
2
E
)
2
E
i
n
i
t
i
a
l
=
4
1
C
E
2
After the switch is closed,Energy residing in the capacitors
E
f
i
n
a
l
=
2
1
C
(
E
)
2
+
2
1
C
(
2
E
)
2
E
f
i
n
a
l
=
2
5
C
E
2
Energy supplied by the batteries
E
b
a
t
t
e
r
i
e
s
=
(
2
3
C
E
)
E
+
(
2
3
C
E
)
2
E
E
b
a
t
t
e
r
i
e
s
=
2
9
C
E
2
E
i
n
i
t
i
a
l
+
E
b
a
t
t
e
r
i
e
s
−
E
f
i
n
a
l
=
2
1
L
i
m
a
x
2
Solving the equation gives
i
m
a
x
=
2
3
E
L
C
@Steven Chase @Karan Chatrath Have a look
@Krishna Karthik Thanks ,love you bro
Log in to reply
No problem. Btw I really need to learn about circuitry.
Current through right capacitor I 2 and that through left capacitor is I 1 . Charge on left capacitor is Q 1 and that through right capacitor is Q 2 . CUrrent through coil is I .
Circuit equations:
− E + C Q 1 + L I ˙ = 0 − 2 E + C Q 2 + L I ˙ = 0 I = I 1 + I 2 Q ˙ 1 = I 1 Q ˙ 2 = I 2
Let I ( 0 ) = Q 1 ( 0 ) = Q 2 ( 0 ) = 0
Laplace transform on both sides:
− s E + C Q 1 ( s ) + L s I ( s ) = 0 − s 2 E + C Q 2 ( s ) + L s I ( s ) = 0 I ( s ) = I 1 ( s ) + I 2 ( s ) s Q 1 ( s ) = I 1 ( s ) s Q 2 ( s ) = I 2 ( s )
Solving for I ( s ) gives:
I ( s ) = 2 3 E L C ⎝ ⎛ s 2 + 2 L C 1 2 L C 1 ⎠ ⎞
Taking inverse Laplace transform gives:
I ( t ) = 2 3 E L C sin ( 2 L C t )
Therefore:
I m a x = 2 3 E L C
@Karan Chatrath can we solve this without laplace?
Log in to reply
Yes, this can be easily solved without Laplace. The differential equations need to be rearranged in a certain way.
Log in to reply
@Karan Chatrath
yes I am doing that only.
See my note, how to proced, please help
See the diagram above for the polarity and naming conventions. The state variables are the capacitor voltages V C 1 and V C 2 , and the inductor current I L .
The first equation is for the inductor.
V L = L I ˙ L E + V C 1 = L I ˙ L
The next equation relates two different expressions for the voltage across the inductor:
E + V C 1 = 2 E − V C 2
Taking the time derivatives of both sides yields an expression in terms of the time derivatives of the capacitor voltages.
V ˙ C 1 = − V ˙ C 2 V ˙ C 1 + V ˙ C 2 = 0
Finally, the sum of the capacitor currents (expressed in terms of the capacitor voltages) equals the inductor current. Note that due to the polarity convention used, the Capacitor 1 current is negated.
I C 2 − I C 1 = I L C 2 V ˙ C 2 − C 1 V ˙ C 1 = I L
To summarize:
E + V C 1 = L I ˙ L V ˙ C 1 + V ˙ C 2 = 0 C 2 V ˙ C 2 − C 1 V ˙ C 1 = I L
In matrix form (note that C 1 and C 2 are equal to C ):
\[\begin{bmatrix} L & 0 & 0 \\ 0 & 1 & 1 \\ 0 & -C_1 & C_2 \end{bmatrix}
\begin{bmatrix} \dot{I}_L \\ \dot{V}_{C1} \\ \dot{V}_{C2} \end{bmatrix}
= \begin{bmatrix} E + V_{C1} \\ 0 \\ I_L \end{bmatrix} \]
This is a state-space representation in which the time derivatives of the state variables are expressed in terms of the state variables and the forcing functions (the voltage sources, in this case). One could try and solve this system of differential equations analytically. I used numerical integration instead.
Since the overall voltage across both capacitors in series is initially E , initialize the state variables as follows:
V C 1 ( 0 ) = 2 E V C 2 ( 0 ) = 2 E I L ( 0 ) = 0
The constant α ≈ 2 . 1 2 1 .