A Nice Inequality
2 a + b 1 + 2 b + c 1 + 2 c + a 1 If a , b and c are positive reals satisfying a 1 + b 1 + c 1 = 1 , find the maximum value of the expression above.
Submit your answer to 3 decimal places
The answer is 0.333.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
How did you arrive at the first inequality?
Log in to reply
By applying Cauchy-Schwarz Inequality
How did you use Cauchy-Schwarz in the first line? Could you explain in full?
a + b + c ≥ 9 and a + b + c ≥ 3 3 a b c doesn't make a b c = 2 7
Log in to reply
From (2) and AM-GM inequality,minimum of a+b+c is 9=3 x abc^(1/3) .Can you explain in what light you are trying to say that?
Log in to reply
try a = 1 9 3 0 ; b = 6 ; c = 5 , then a + b + c ≥ 9 and a + b + c ≥ 3 3 a b c still holds true but a b c = 2 7 is wrong. By saying a b c = 2 7 , you are assuming a = b = c
By Titu's Lemma ,
a 1 + a 1 + b 1 ≥ 2 a + b 9
b 1 + b 1 + c 1 ≥ 2 b + c 9
c 1 + c 1 + a 1 ≥ 2 c + a 9
Adding all gives ,
a 3 + b 3 + c 3 ≥ 2 a + b 9 + 2 b + c 9 + 2 c + a 9
⇒ 9 3 = 3 1 ≥ 2 a + b 1 + 2 b + c 1 + 2 c + a 1
Equality holds when a = b = c = 3
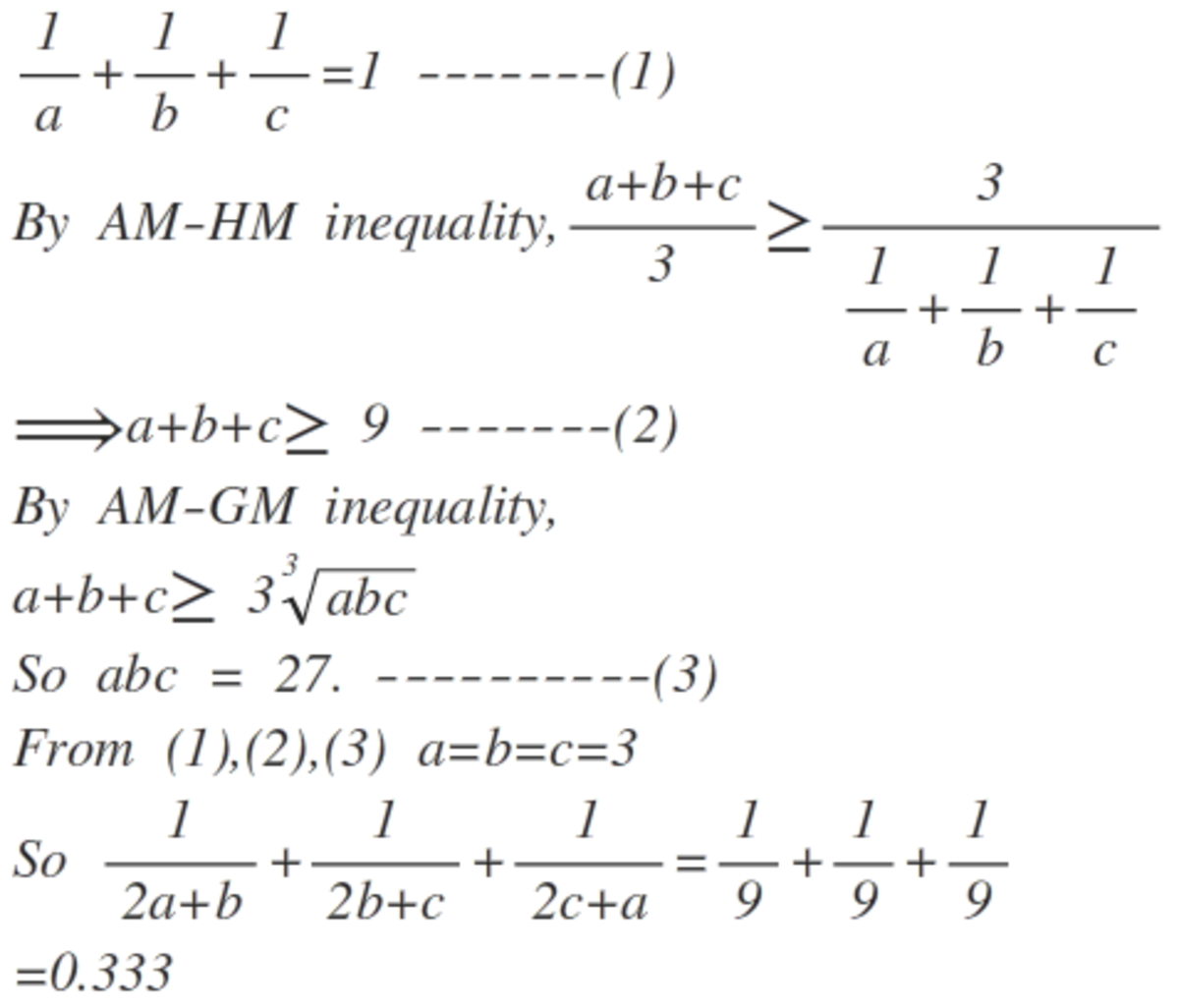
Call the expression M we have 2 a + b 9 ≤ a 1 + a + b 4 ( T i t u ′ s L e m m a ) Doing the similar to the others then combine 3 inequalities, we have 9 M ≤ 1 + a + b 4 + b + c 4 + a + c 4 ≤ 3 ( A M − H M ) ⇔ M ≤ 3 1 The equality holds when a = b = c = 3