Inequality 2017

Algebra Level 4

$\sqrt { \frac { { a }^{ 3 } }{ { a }^{ 3 }+15bcd } } +\sqrt { \frac { { b }^{ 3 } }{ { b }^{ 3 }+15cda } } +\sqrt { \frac { { c }^{ 3 } }{ c^{ 3 }+15dab } } +\sqrt { \frac { { d }^{ 3 } }{ d^{ 3 }+15abc } }$

Find the minimum value of the expression above, where $a$ , $b$ , $c$ and $d$ are positive real numbers.

The answer is 1.

2 solutions

Ciprian Florea
Apr 10, 2017

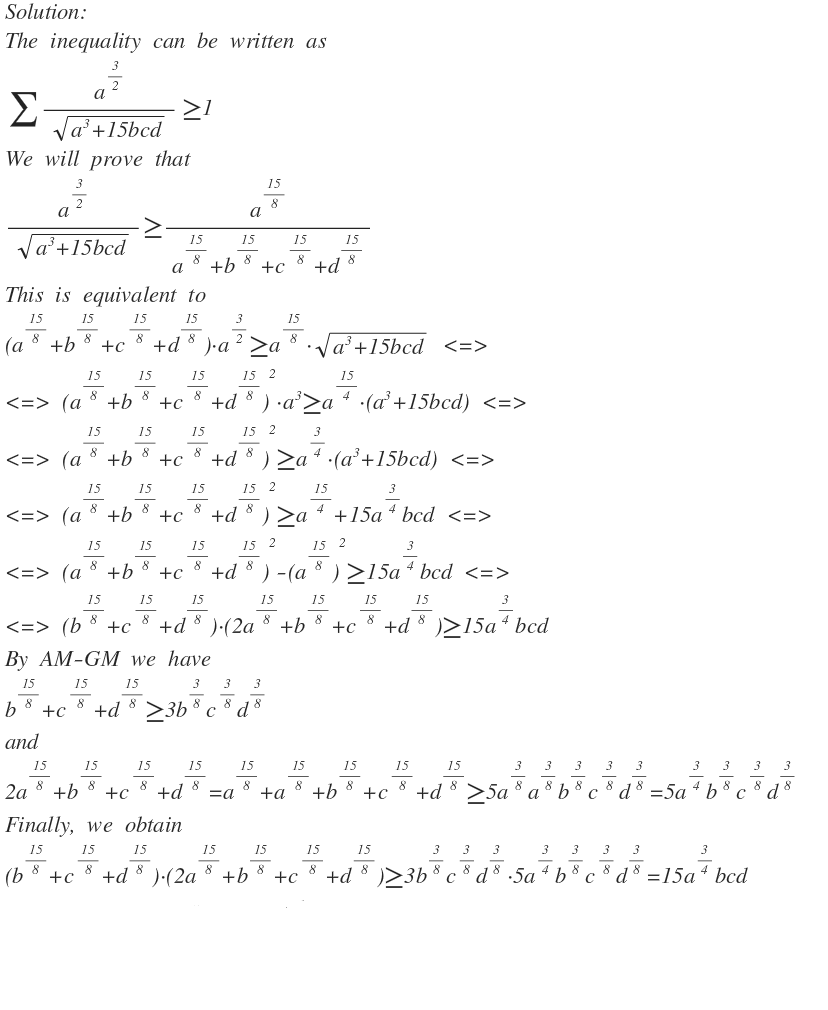
Reminds me of IMO 01/2, which had a similar proof.

Calvin Lin Staff - 4 years, 2 months ago

Exactly, it was inspired from there.

Ciprian Florea - 4 years, 2 months ago

Do you have a clear idea on how to come up with that initial "fudging" inequality? IN my opinion, it always seems very magical as to how they obtain the bound. E.g. if 15 became 80, then I don't know what to try next.

Calvin Lin Staff - 4 years, 2 months ago

I Upvoted your solution as brilliant, interesting, and helpful! I see a typo though. It says $b^\frac{15}{8}+c^{\frac{15}{8}}+d^{\frac{15}{8}}\geq 3a^\frac{3}{8}b^\frac{3}{8}c^\frac{3}{8}$ , when it should say $b^\frac{15}{8}+c^{\frac{15}{8}}+d^{\frac{15}{8}}\geq 3a^\frac{5}{8}b^\frac{5}{8}c^\frac{5}{8}$ . Note: the typo does not affect the correctness of the solution.

James Wilson - 5 months ago

Chew-Seong Cheong
Apr 11, 2017

$\color{#D61F06} \text{Sorry, the solution is incorrect.}$

Using AM-GM inequality , we have:

$\small \begin{aligned} \sqrt {\frac {a^3}{a^3+15bcd}} + \sqrt {\frac {b^3}{b^3+15cda}} + \sqrt {\frac {c^3}{c^3+15dab}} + \sqrt {\frac {d^3}{d^3+ 15abc}} & \ge 4 \sqrt [8] {\frac {a^3}{a^3+15bcd} \times \frac {b^3}{b^3+15cda} \times \frac {c^3}{c^3+15dab} \times \frac {d^3}{d^3+ 15abc}} \\ & \ge 4 \sqrt[8]{\left(\frac 1{16} \right)^4} \quad \quad \color{#3D99F6} \text{Equality occurs when }a =b=c=d \text{ (see note).} \\ & \ge \boxed{1} \end{aligned}$

Note: Equality occurs when:

$\small \begin{aligned} \sqrt {\frac {a^3}{a^3+15bcd}} = \sqrt {\frac {b^3}{b^3+15cda}} & = \sqrt {\frac {c^3}{c^3+15dab}} = \sqrt {\frac {d^3}{d^3+ 15abc}} \\ \implies a = b & = c = d \\ \implies 4 \sqrt [8] {\frac {a^3}{a^3+15bcd} \times \frac {b^3}{b^3+15cda} \times \frac {c^3}{c^3+15dab} \times \frac {d^3}{d^3+ 15abc}} & = 4 \sqrt [8] {\frac {a^3}{a^3+15a^3} \times \frac {b^3}{b^3+15b^3} \times \frac {c^3}{c^3+15c^3} \times \frac {d^3}{d^3+ 15d^3}} \\ & = 4 \sqrt [8] {\frac 1{16} \times \frac 1{16} \times \frac 1{16} \times \frac 1{16}} \\ & = 4 \sqrt [8] {\left(\frac 1{16} \right)^4} \end{aligned}$

Could you please explain the last part of the inequality? The one after you used AM-GM..

Ciprian Florea - 4 years, 2 months ago

I have added it in the note.

Chew-Seong Cheong - 4 years, 2 months ago

Unfortunately that is not correct.

Yes, it is true that
1. $\sum \sqrt{ a^3} { a^3 + 15 bcd } \geq 4 \prod \sqrt[4] { a^3 } { a^3+15bcd }$
2. Equality holds when $a = b = c =d$ .
3. When $a = b = c = d$ , then $4 \prod \sqrt[4] { a^3 } { a^3+15bcd } = 1$

However, that doesn't mean that $\sum \sqrt{ a^3} { a^3 + 15 bcd } \geq 1$ . Let me break it down why. What we have is:
1. $f(x) \geq g(x)$
2. Equality occurs at $x = x^*$ .
3. $g(x^*) = M$

Then, you are claiming that $f(x) \geq M$ . Do you see why this is not true? Are there obvious counter examples of $f(x), g(x)$ ?

Calvin Lin Staff - 4 years, 2 months ago

@Calvin Lin – Thanks. I get what you mean. But I can't find a counter example. If you can help. I always have problems with this.

Chew-Seong Cheong - 4 years, 2 months ago

@Chew-Seong Cheong – Counter example:
Take $f(x) = 2x^2 + x$ , $g(x) = x^2 + x$ .
Clearly $f(x) \geq g(x)$ .
Equality holds when $x^* = 0$ .
We have $g(0) = 0$ .
However, the minimum of $f(x)$ is not 0.

Looking at the graphs should give you a clearer picture of what is happening. Right now, we have $f(x) \geq g(x)$ , but no relationship between $g(x)$ and $g( x^* )$ . Becuse of that. it's possible to have some $x_0$ such that $g( x_0) < f( x_0) < g( x^* ) = M$ , as seen in the counter example.

In order to conclude that $f(x) \geq M$ , one possible condition to also requires is that "The minimum of $g(x)$ occurs at $x = x^*$ ". In that scenario, we then have the chain of inequalities $f(x) \geq g(x) \geq g( x^*) = M$ .

Calvin Lin Staff - 4 years, 2 months ago

@Calvin Lin – Thanks a lot.

Chew-Seong Cheong - 4 years, 2 months ago

Inequality 2017

The answer is 1.

2 solutions

0 pending reports