But none them resembles me!
2 a 3 ( b + c ) + 3 b 4 a + 3 c + 2 a + 3 c 1 2 ( b − c )
If a , b and c are positive real numbers, find the minimum value of the expression above.
Bonus : Find the values of a , b and c when the expression above is minimized.
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
how to know that the equality hold when p=q=r/2?
I 'm the head master, i created the problem .Just let you know, there are at least 6 solotions for this problem when i created it. Here is one that easily seen by anyone:
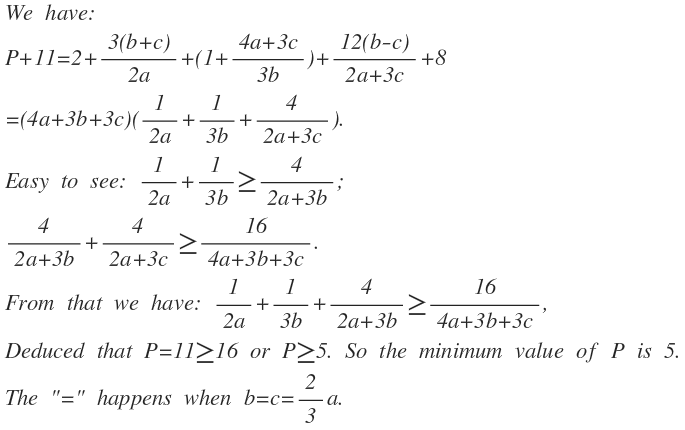
Interesting problem. Who were you creating this problem for?
Log in to reply
My friend, he co-found this problem, he did the math, i did the change.
The minimal point occurs when a = 2b/3 = 2c/3. Consider (2,3,3). What you have written in the last line is incorrect. It should be b = c = 3a/2 or a = 2b/3 = 2c/3.
Let x = 2 a 3 b + 3 c + 3 b 4 a + 3 c + 2 a + 3 c 1 2 b − 1 2 c .
Let a 1 = 2 a , b 1 = 3 b , c 1 = 2 a + 3 c .
By AM - GM we have x = a 1 b 1 + c 1 − a 1 + b 1 a 1 + c 1 + c 1 4 [ a 1 + b 1 − c 1 ] = a 1 b 1 + a 1 c 1 + b 1 a 1 + b 1 c 1 + c 1 4 a 1 + c 1 4 b 1 − 5 ≥ 5 .
Start by assuming that b = c. The motivation for this is simple, because we are trying to minimize the above expression, setting b-c = 0 allows us to get rid of the third term of the expression. Doing so also allows us to now minimize an expression that is in terms of two variables rather than three variables. So, we are trying to minimize 3b/a + 4a/3b + 1. Now, the simplest way to make 3b/a an integer is to allow the variable a to equal the minimum positive multiple of 3, which is 3. Letting a = 3 simplifies and minimizes our expression to b + 4/b + 1. Taking the derivative of this expression and setting it equal to zero allows us to find the critical points of the function to be b = +/- 2, but since a,b,c > 0, we know that b = 2. Now c = 2 since b = c, and it follows that (2,3,3) is the minimum point at which the expression is minimized. Thus, min(f(a,b,c,)) = f(2,3,3) = 5.
More generally, the minimal point happens when b = c and a = 2b/3 = 2c/3! Trivial!
The given expression can be written as :
[ 2 a 3 b + 3 b 2 a ] + 2 a 3 c + [ 3 b 2 a + 3 c + 2 a + 3 c 1 2 b ] − 2 a + 3 c 1 2 c
Applying AM GM inequality inside the brackets we get :
[ 2 a 3 b + 3 b 2 a ] + 2 a 3 c + [ 3 b 2 a + 3 c + 2 a + 3 c 1 2 b ] − 2 a + 3 c 1 2 c ≥ 6 + 2 a 3 c − 3 a + 2 c 1 2 c
The equality occurs when 2a = 3b = 3c
[ 2 a 3 b + 3 b 2 a ] + 2 a 3 c + [ 3 b 2 a + 3 c + 2 a + 3 c 1 2 b ] − 2 a + 3 c 1 2 c ≥ 1 + 2 a 3 c + 4 − 2 a + 3 c 1 2 c + 1
[ 2 a 3 b + 3 b 2 a ] + 2 a 3 c + [ 3 b 2 a + 3 c + 2 a + 3 c 1 2 b ] − 2 a + 3 c 1 2 c ≥ [ 2 a 2 a + 3 c + 2 a + 3 c 8 a ] + 1
Again applying AM GM inequality inside the brackets we get:
[ 2 a 3 b + 3 b 2 a ] + 2 a 3 c + [ 3 b 2 a + 3 c + 2 a + 3 c 1 2 b ] − 2 a + 3 c 1 2 c ≥ 4 + 1
Equality occurs when 2a = 3c
Hence the minimum value of the above expression is 5
The inequality is homogenous then we can suppose b=c By AM-GM the result is obvious
No, you cannot suppose that b=c, even though it is homogeneous.
What you could do is assume that a + b + c = 1 or that a b c = 1 . There is no reason to assume that b = c .
Log in to reply
i see,thanks
Log in to reply
As a,b,c are positive reals we can minimize the last part by putting b=c.The other two part can not be simplified because they will be b=-c and 4a=-3c.It is not possible because a,b,c are positive.
Log in to reply
@Kushal Bose – No, that is a very common mistake to make. It is not always true that "the minimum of f ( x ) + g ( x ) occurs at the minimum of f ( x ) or the minimum of g ( x ) ". There is apriori no reason why we want to minimize the third part.
Also, note that 0 isn't the minimum of the third part, since it could be negative with c > b .
L e t 2 a = p , 3 b = q , 2 a + 3 c = r p , q , r a r e l i n e a r l y i n d e p e n d e n t . N o w , 2 a 3 ( b + c ) + 3 b 4 a + 3 c + 2 a + 3 c 1 2 ( b − c ) = p q + r − p + q p + r + r 4 ( q − r + p ) = p p + q + r − 2 + q p + q + r − 1 + r 4 ( p + q + r ) − 8 = p p + q + r + q p + q + r + r 4 ( p + q + r ) − 1 1 b u t A M ≥ H M ∴ 4 p + q + 2 × 2 r ≥ p 1 + q 1 + 2 × r 2 4 ⇒ p p + q + r + q p + q + r + r 4 ( p + q + r ) ≥ 1 6 ⇒ p p + q + r + q p + q + r + r 4 ( p + q + r ) − 1 1 ≥ 5 e q u a l i t y h o l d f o r p = q = 2 r