Quadratic With Inequality Insane Level!
 The values of
k
for which the inequality
k
⋅
(
x
+
6
)
x
2
+
k
2
≥
1
is satisfied by all
x
∈
(
−
1
,
1
)
are
[
a
,
∞
)
.
The values of
k
for which the inequality
k
⋅
(
x
+
6
)
x
2
+
k
2
≥
1
is satisfied by all
x
∈
(
−
1
,
1
)
are
[
a
,
∞
)
.
Find the value of a (round off up to 3 decimal places).
The answer is 6.854.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice solution! +1
Why 400 pts?
This question required deep analysis of the function.
When I saw the question I thought of proceeding by substituting x by sinx. Can you tell me how I should proceed so that I get the answer.
The other possibility yields k^2>8
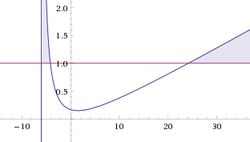
The problem can be solved by plotting f ( x , k ) = k ( x + 6 ) x 2 + k 2 for x ∈ ( − 1 , 1 ) for various k and inspect. It can be easily done with a spreadsheet.
The following shows the curves for integer k from − 2 to 8 except 0 .
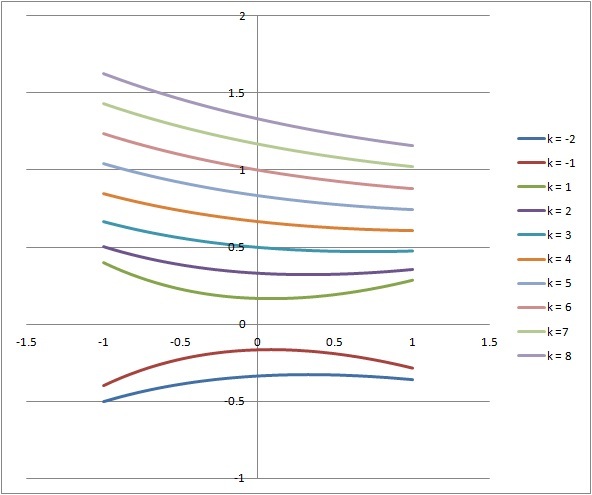
It can be seen that the smallest k , that is a is slightly smaller than 7 and that f ( x , a ) = 1 , that is the lowest point, when x = 1 . Therefore,
a ( 1 + 6 ) 1 2 + a 2 = 1 ⇒ a 2 − 7 a + 1 = 0 ⇒ a = 6 . 8 5 4 (the other smaller root is unacceptable).
can you explain why it happens i.e. why f(1,k) s the lowest point ? how do i know if i do not use a spreadsheet that f(1,k) would be least using mathematical arguments ? it would be great ! :)
i solved it my third attempt :( , can you help what was wrong with my approach , i thought if the function i.e x 2 + k 2 − k x − 6 k ≥ 0 is increasing , and moreover it has positive value for x=-1 , i can say it would be greater than equal to 0 for x=1 too .....and the given condition would be satisfied, so , i put x=1 and obtained the values for k , put x=-1 , obtained values of k and derivated it and put greater then zero , , the answer i got was for the equation in which i put x=1 , this was how i got the answer !
@Mark Hennings @Chew-Seong Cheong @Sandeep Bhardwaj
Check your arithmetic. What is k ⋅ ( x + 6 ) ?
Log in to reply
my arithmetic is alright but my latex is not , i just copy -pasted it from @Mvs Saketh 's solution ! can you figure out what went wrong with the logic i thought of ? thanks for seeing it sir @Calvin Lin
Log in to reply
True or false:
- If a ≥ b then a + c ≥ b + c .
- If a ≥ b then a c ≥ b c .
Log in to reply
@Calvin Lin – true if a,b,c >0
Log in to reply
@A Former Brilliant Member – Right. How does this apply to your solution? In particular, what is the mistake that you made?
As x only varies from ( − 1 , 1 ) , so x + 6 > 0
now if k < 0 , then the situation is not possible which one can easily check himself/herself in two steps, So let us move on,
if k > 0 , then we can simply move the denominator to the right and we get the quadratic
x 2 + k 2 − k x − 6 ≥ 0
Now there are two ways for this and we must check both cases
c a s e ( a ) - the equation has roots but no root lies between [-1,1] and further that the minima point 2 a − b lies outside [-1,1}
since k ≥ 0 so we automatically need 2 k ≥ 1 so k ≥ 2
also we need f ( − 1 ) f ( 1 ) ≥ 0
or ( k 2 − 7 k + 1 ) ( k 2 − 5 k + 1 ) ≥ 0
we simply have to observe that this is positive for large k and as we approach along the number line from ∞ will first become negative at the largest root of the equation, which is the greater root of the 1st quadratic namely 2 7 + 3 5
so k ≥ 2 7 + 3 5
which is answer
checking the other possibility where the equation has no root yields k ≥ 8 which is clearly larger than 2 7 + 3 5 and hence is not the answer