Infinite Atwood’s machine
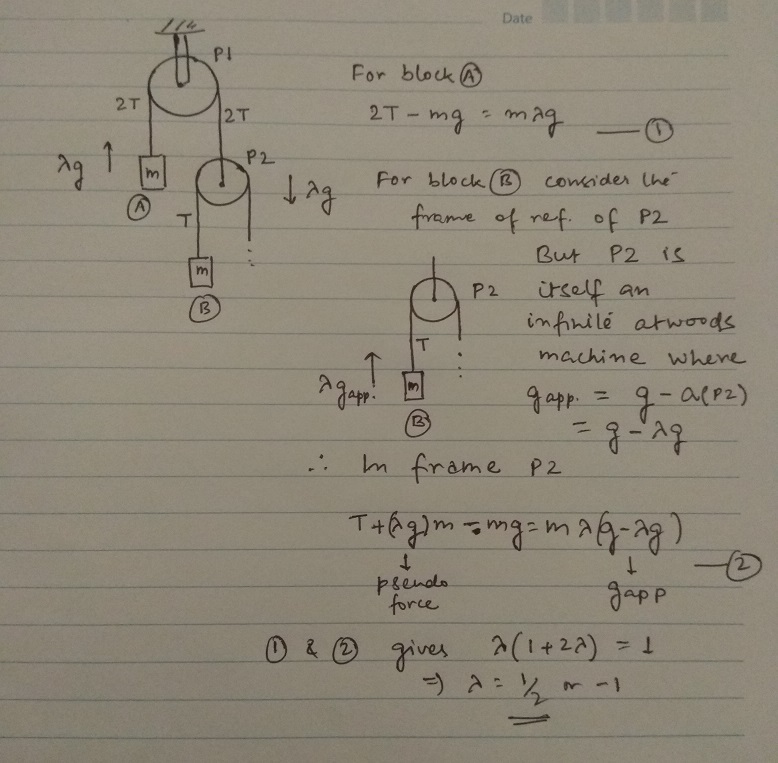
The infinite Atwood’s machine shown has a string passing over each pulley, with one end attached to a mass and the other end attached to another pulley.
The masses are held fixed and then released simultaneously, and the acceleration of the top mass is λ g .
What is λ ?
Details and Assumptions:
- All the masses are equal to M .
- All the pulleys and strings are massless.
- g is the acceleration due to gravity.
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
.5 is such a specific and tidy number for a question involving 2 objects. It reminds me of slopes in high school geometry. If you have 2 objects x and y, and 2 positions for each, you can substitute 'effective mass' for x2-x1 + y2-y1 which kind of equals 4 elements for 2 objects, or .5 'objects' (4/2) if we define objects by 'things doing things' (action/work/motion/discretion) ...effective mass = g = subtracting one line from another. I didn't have any knowledge of newton's laws, so this is my weird way of answering the question using an idiot's intuition. I was thinking of Claude Shannon here.
Are we actually sure that λ = 0 . 5 ? I am new here, and I'm not exactly sure how does this works.
I get λ = 1 (please see below) and I don't get what I'm doing wrong.
The physics/intuitive argument goes like this:
-
Imagine you have a finite number of pulleys.
-
on the last pulley you do not hang any counterweight or just a massless pulley & string with no mass M hanging (otherwise you just added one extra pulley which then becomes the last).
-
Since there is no counterweight there will be no tension on the string of the last pulley and the mass M will just free fall.
-
No tension on the last pulley means there will also not be any tension on the string of the pulley just above, and its mass will also just free fall, pulling with it the massless last pulley.
-
This domino effect propagates till the 1st pulley (the upper one) and all masses M in all pulleys will just free fall.
-
Finally you can keep adding pulleys to the end of the all thing and repeat the argument again.
The physics/mathematical argument goes like this:
1) For any given pulley the scenario is the same, i.e. every pulley has on its left side a mass M hanging and on the right side an infinite number of pulleys and therefore the string tension in 2 consecutive (any) pulleys should be equal: T n = T n+1
2) On the other hand on 2 consecutive pulleys the tension of the above pulley should be twice the one from below: T n = 2 T n+1
3) T n = T n+1 = 0 is the only solution that meets both 1) and 2)
4) But since T = 2 g M + m x M . m x => m x = 0
5) Since a = g M + m x M − m x then a = g
Log in to reply
I thought the answer would be either 1 or 0. My first answer was 1.
Your physical assumption number 1 is wrong. The scenario is not the same for all the pulleys as the first first pulley is attached to the ceiling, so its acceleration is 0, while the other pulleys are accelerating (with different accelerations). However apart from the accelerations the sceneario is the same. In fact you might use this to get the answer. Remember in an accelerated frame of reference the frames acceleration corresponds to a gravitational force.
Look at the first mass. From Newtons second law you get the tension in string number 1 is
T
1= mg*(1+\lambda). Remember the mass is accelerating upwards.
Pulley number 2 is accelerating downwards with the acceleration \lambda g (as the first mass is accelerating upwards and pulley 1 is lying still). So the effective gravitational acceleration in a frame attached to pulley number 2 is g
eff = g
(1- \lambda). As before (pulley 2 is sitting at rest in this accelerated frame) the tension in string number 2 is T_2 = m g_eff * (1 + \lambda) = m g * (1-\lambda)(1+\lambda). This expression for the tension is also correct in all other frames classically.
AS you state in your assumption number 2 from Newtons second law on the massless pulley number 2 is T_1=2
T
2.
Plugging in T
1= mg
(1+\lambda) and T_2 = m g * (1-\lambda)(1+\lambda) you get
1=2
(1-\lambda) (or \lambda = -1, which physically is a strange solution) and thus
\lambda = 1/2
Log in to reply
there are two answers, at least what I can think of so far, one is DOWNWARD acceleration g (i.e., \lambda=-1) for ALL mass and the tension in all string is ZERO. You can't find anything physically wrong with this answer. In fact if you approach the problem with a finite system, and keeping adding more and more pulley/mass to it, this is answer you will have (Imagine you have just one pulley and one mass, and release the sting from the right, and then go to the 2 pulley/ 2 mass one and do the same). The issue with this answer is that the relative acceleration between the pulley and the mass attached to it grows unbounded as you go downward.
The second solution is that first mass has an UPWARD acceleration 1/2g (i.e., \lambda=+1/2), and the accelerations of the subsequent masses are all different but they approach the limit of -g (i.e., DOWNWARD) as you keep going to the bottom of the system. In this solution the relative accelerations are all bounded. The solution is nicely written by Mark Hennings below.
You said that "\lambda = -1, which physically is a strange solution". This is NOT true. In fact, this is a more physically realistic solution for the following reason: the system depicted in this problem almost surely does NOT exist in the physically world! If you do an experiment with a realistic physical approximation to it, that is, a system with a large (but FINITE) number of components, you actually get \lambda = -1! Because the tension of the string attached to the last mass at the bottom is zero (or almost zero in experiment), and when you back propagate this to the top (for a FINITE number of stages), the tension will still be zero (or almost zero in experiment).
In my point of view, this is a textbook example of a singular problem where the answers to a family of finite models do not converge to the BOUNDED answer in the infinite model (the limiting case of the family of finite models).
Log in to reply
@Dennis Y – Thanks Dennis Y and Kasper Astrup Eriksen for your replies.
I now understand how the lambda=0.5 result is reached (which it is not very clear in the most upvoted comment) but, most importantly, that there are 2 solutions to the problem. My intuition was not so completely wrong after all :)
I feel that your two comments should be the most upvoted, not only b/c they explain better the standard/wanted solution of 0.5, they also bring up the issue of the 2nd (not so standard) solution which is is, in my opinion, very eye opening.
Log in to reply
@P S – You might want to look at my comments to Dennis Y following my solution. At the bottom line, the whole problem is unrealistic, and both solutions have their problems!
I don't get it ...
Yeah... I don't know how to do that first step.
Where did you get the equation for the effective mass from? I have never heard of that before.
For the first expression, why the 4 factor? I don't get this factor when I do it
Log in to reply
Read the proof of effective mass, I have added it now.
Log in to reply
Excellent copy-and-paste...
Log in to reply
@Mark Hennings – Yeah...lol... I left it because i didnt have time to write the proof, but now you wrote it so i copied and pasted!
Since a number of people are confused about this effective mass thing, here is a derivation...
If a pulley system is suspended with masses M 1 , M 2 on each side, then we have M 1 g − T = M 1 a T − M 2 g = M 2 a where T is the tension in the string, and a is the acceleration of the particles. Eliminating a , we deduce that T = M 1 + M 2 2 M 1 M 2 g Thus the tension in any string supporting the pulley must be 2 T = M 1 + M 2 4 M 1 M 2 g and so the effect on the system above the pulley would be the same if the pulley system was replaced by a mass of M 1 + M 2 4 M 1 M 2 .
I can't tell how I felt on reading this. My method was - Take the case of n strings, obtain n equations with variables as the accelerations of each pulley as seen by the one above it and the tension of the bottommost string.. Then I used Cramer's rule to get my answer for the tension of the topmost string as the ratio of two n×n matrices. After evaluating them my answer was [3{2^(2n-2)}]/{2^(2n-1)-1} mg . I made n tend to infinity to get that tension as 3mg/2. And then only did I get the upward acceleration of g/2. And then I found THIS.
This answer is INCORRECT.
In your setup, the positive direction of "a" for M1 is DOWNWARD, hence a = 1/2 g means that the first mass accelerates downward.
The correct answer (with bounded relative acceleration in the system) is that the first mass accelerates UPWARD with 1/2g. See the correct solution given by Mark Hennings. He defines x1 to be the distance between the first mass and first pulley, so the second derivative of x1 is -1/2g in his solution means that the first mass accelerates upward.
Log in to reply
Well, the sign doesn't really matters. We clearly know that the block has to accelerate upwards, What I have shown is the magnitude, If you will try to solve the problem by writing correct equations assuming proper direction, you will get a correct result.Your claim that the sign of my calculated acceleration is positive doesn't imply my solution is wrong.
Could the solution also be downward g? If there was a finite chain of pulleys and weights the lowest would have T=0 as there was no counterweight, if this is true, no number of additional steps would add any mass at all, you need an initial mass even of 10^-100 but you don't have that in a finite solution. Why should there be a initial counterweight in an infinite one? (This would lead to very low pulley setups to be over the speed of light practically instantly so not realistic)
Suppose that all the strings have length L , and let x j be the distance of the j th mass (for j ≥ 0 ) from the j th pulley. Then the distance of the j th mass below the top ( 0 th) pulley is d j = x j + k = 0 ∑ j − 1 ( L − x k ) = j L + x j − k = 0 ∑ j − 1 x k for j ≥ 1 , so that d ¨ j = x ¨ j − k = 0 ∑ j − 1 x ¨ k ( j ≥ 1 ) d ¨ 0 = x ¨ 0 If the tension in the j th string is T j then, since the j th pulley is weightless, T j − 1 = 2 T j , and so we can write T j = M τ 2 − j j ≥ 0 The equation of motion of the j particle is M d ¨ j x ¨ j − k = 0 ∑ j − 1 x ¨ k = M g − T j = g − τ 2 − j Thus x ¨ j + 1 − 2 x ¨ j = ( x ¨ j + 1 − k = 0 ∑ j x ¨ k ) − ( x ¨ j − k = 0 ∑ j − 1 x ¨ k ) = τ 2 − j − 1 and we can solve this recurrence relation, together with x ¨ 0 = g − τ , to deduce that x ¨ j = 2 j [ g − 3 2 τ − 3 1 τ 2 − 2 j ] j ≥ 0 Since these accelerations need to remain bounded, we deduce that τ = 2 3 g , so that d ¨ 0 = x ¨ 0 = − 2 1 g , making the answer 2 1 .
\tau = 0 (which mean all masses accelerate DOWNWARD at g and all tensions are ZERO) is another solution, but is neglected in the last step of your derivation in order to keep \ddot{x}_j bounded, which is of course every reasonable to do for this problem.
However, \tau = 0 is a more physically realistic solution for the following reason: the system depicted in this problem almost surely does NOT exist in the physically world! If you do an experiment with a realistic physical approximation to it, that is, a system with a large (but FINITE) number of components, you actually get \tau = 0! Because the tension of the string attached to the last mass at the bottom is zero (or almost zero in experiment), and when you back propagate this to the top (for a FINITE number of stages), the tension will still be zero (or almost zero in experiment).
In my point of view, this is a textbook example of a singular problem where the answers to a family of finite models do not converge to the BOUNDED answer in the infinite model (the limiting case of the family of finite models).
Log in to reply
The real problem is that this problem is totally unrealistic - where are you going to lay your hands on an infinite number of pulleys?
In the τ = 0 solution, x ¨ j is an unbounded sequence, and that means that somewhere down the system the pulleys would be rotating so fast that points in their rims were exceeding the speed of light. At least the "everything remains bounded" solution avoids that nonsense.
Log in to reply
If you were really to bring in the constraint due to the "speed of light" and do everything in that realm, then your whole derivation would become invalid too! There is NO instantaneous interactions, the strings can only propagate force at a speed no faster than light.
Log in to reply
@Dennis Y – There are plenty of examples of problems where you cannot obtain the infinite case by taking the limit of the finite case. Imagine trying to build a bridge over a river of length 1 by adding bricks of length 1 / 2 , 1 / 4 , 1 / 8 ,... If you only use a finite number of bricks, your bridge will fall into the river. If you could use an infinite number of bricks, you could span the river, and the bridge would stand up.
You are arguing that the finite analogy has to rule. I am pointing out that there are logical faults to that case, just as there are logical faults (namely impossibility) to the infinite. Since this problem is inherently unrealistic, we might as well leave things here, since noone will ever build a model to test the experiment!
Were the first mass not moving at all, that would apply that the first pulley (not the one hanged to the ceiling) doesn't accelerate, and the tension of the first string equals mg. Hence, the tension of the second string, which equals half the first string, is 2 g m
Solving the motion equation for the second mass, we get that its acceleration is 2 g
But what we've got here is actually the same problem as was presented!
That's true because the first pulley doesn't move, that is, it behaves as a ceiling. And there are infinite masses connected to the second mass from the right side, that is, the same situation as for the first mass.
Therefore we deduce that the acceleration of the first mass is 2 g
I am not getting it... Please tell me how you arrived at the first step
The method is incorrect - because the net acceleration of the first mass is upwards. Your method gives it downwards.
Looking the top mass you have a force Mg pulling down and the force from the series of pullys pulling up.
The net force can be written as F=Mg-(Mg-(Mg-...
Divide by factor M to get, a=g-(g-(g-...
This can be written at a=g-a.
Solve a=(1/2)g.
lambda = 1/2
I really like the way you coped with the infinite series. I used ma=mg(1-1+1-1+1-...) and used the convergent value of the series. Yours feels more elegant.
I know Physics more than Maths, so I prefer this solution because of this reason and I saw a BRILLIANT version of solution in an other weekly problem where an infinite sum is written to a form like your a=g-a. That was amazing, thank you!
Let us inspect the pulley hung directly from the ceiling. We can imagine that the pulley is supporting two masses, one on either side.
The mass on the left has a mass of M and the mass on the right n M , where n represents the total number of masses on that side - since they are all part of the system, their individual masses will add up.
We are now ready to construct equations from Newton's law of motion. Let's start from the left-hand side first.
(We are going to set the direction in which the right-hand side masses are moving as positive.)
T − M g = ( n + 1 ) M a
and the right-hand side:
n M g − T = ( n + 1 ) M a
Add both equations together.
( n − 1 ) M g = 2 ( n + 1 ) M a
Divide both sides by M
g ( n − 1 ) = 2 a ( n + 1 )
Rearrange so that a became the subject.
a = 2 ( n + 1 ) g ( n − 1 )
When n → ∞ :
2 ( n + 1 ) g ( n − 1 ) → 2 g
Thus, λ = 2 1
Isolate the second mass -- examine its motion relative to the second pulley. It's easy to see that it also has acceleration λ g (with acceleration toward the ground taken in the positive sense) with respect to the pulley, because the pulley setup is infinite and it mirrors the system as a whole. The first mass pulls the pulley upward with force M λ g by Newton's second law, and gravity pulls down with force M g . By Newton's third law, the forces M λ g and M g − M λ g are equal. Setting these two quantities equal and dividing by M g shows us that λ = 0 . 5
The effective mass (or you can call it reduced mass) of 2 blocks of masses M 1 and M 2 hanging from a pulley is given by M effective = M 1 + M 2 4 M 1 M 2
So, attach a block mass x on the string and note that it should be the effective mass of the whole system, so we have the equation x = M + x 4 M x and from here we get that x = 3 M
For the acceleration in this type of system, it is given by the ratio of difference in masses and the sum of the masses times the acceleration due to gravity, so a = ( 3 M + M 3 M − M ) g = 4 M 2 M g = 2 g , hence answer is 0 . 5
I am writing the derivation of the effective mass expression as given by @Mark Hennings in the comments section.
So, If a pulley system is suspended with masses M 1 , M 2 on each side, then we have M 1 g − T = M 1 a T − M 2 g = M 2 a where T is the tension in the string, and a is the acceleration of the particles. Eliminating a , we deduce that T = M 1 + M 2 2 M 1 M 2 g Thus the tension in any string supporting the pulley must be 2 T = M 1 + M 2 4 M 1 M 2 g and so the effect on the system above the pulley would be the same if the pulley system was replaced by a mass of M 1 + M 2 4 M 1 M 2 .
For a , eliminate T from these equations to get a = M 1 + M 2 M 1 − M 2 g