Infinite Limit?
n → ∞ lim ( e 2 1 1 + e 3 2 1 + e 4 3 1 + … + e n n − 1 1 ) = ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
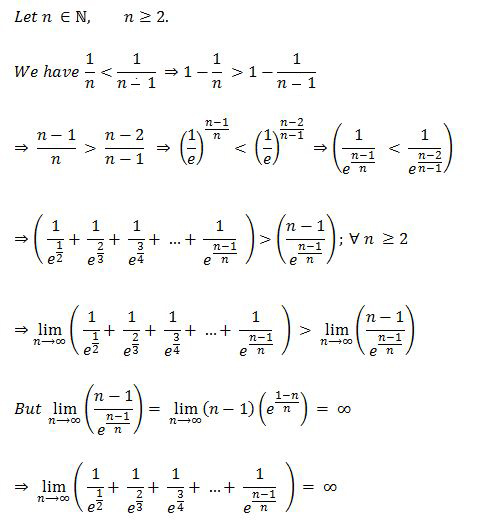
Moderator note:
There's a much simpler approach.
Hint : Consider a n = e − n n − 1 . What happens when we consider the limit n → ∞ lim a n ?
@Challenge Master , the value of that would be e 1 :)
Log in to reply
Hey bro which is greater half or one third.... .
Log in to reply
Wrong solution,kindly review it
Log in to reply
@Suyash Harsh – Hi @Suyash Harsh , Thank you for pointing out my silly mistake. The solution is definitely correct, I only had some typo-error in the second line. Actually, it'd be n 1 < n − 1 1 in the second line. Everything is correct from the third line onwards. :) I've edited the second line of the solution. :)
L L = e 1 / 2 1 + e 2 / 3 1 + e 3 / 4 1 + . . . > e 1 + e 1 + e 1 + . . .
Since the RHS diverges and L > RHS, L diverges, ⟹ L → ∞
n → ∞ lim ( e 1 − 1 / 2 1 + e 1 − 1 / 3 1 + . . . + e 1 − 1 / n 1 )
e 1 n → ∞ lim r = 2 ∑ n e r 1
Now
n → ∞ lim e n 1 = 1
and e 1 / 2 = 1 p o i n t s o m e t h i n g e 1 / 3 = 1 p o i n t s o m e t h i n g and so on
e 1 ( 1 . a b c + 1 . p q r + 1 . x y z + . . . . . i n f i n i t e t e r m s )
Answer is ∞