Infinite Recursive Logarithm Sequence

It is a nice question. As $a_n=\log_{a_{n-1}}{27}$ implies $a_{n-1}^{a_n}=27=3^3$ which means that if the limit exist (says the limit is $\displaystyle\lim_{n \to \infty} a_n = x=\lim_{n \to \infty} a_{n-1}$ , then $x^x=3^3$ ), it must be 3. I have not found any algebraic proof. I used Geogebra and notice that the result will still the same if $1.3 \le a_0 \le 12.73$ , and the limit does not exist if $a_0$ is out of the range. I wish to know why $\lim_{n \to \infty} a_n$ does not exist so such $a_0$ .

Start off by using change of base for logarithms to simplify the problem. $a_n=\log_{a_{n-1}}(27)=\frac{\log(27)}{\log(a_{n-1})}$ Now, let's start calculating the first few numbers in the sequence: $a_0=\pi \\ a_1 = \log_\pi(27)=\frac{\log(27)}{\log(\pi)} \\ a_2 = \log_{\log_\pi(27)}(27)=\frac{\log(27)}{\log(\log_{\pi}(27)}=\frac{\log(27)}{\log(\frac{\log(27)}{\log(\pi)})}$ In this way, we see that the each consecutive term in the sequence embeds the previous term in itself. Therefore, we can redefine the recursive sequence as: $a_0=\pi, a_n=\frac{\log(27)}{\log(a_{n-1})}$ Since infinity is not a number, but a concept, then we have $\lim_{n \to \infty} a_n = \frac{\log(27)}{\log(a_n)}$ Now we can solve for the limit: $a_n = \frac{\log(27)}{\log(a_n)} \\ \log(a_n)\cdot a_n = \log(27) \\ \log((a_n)^{a_n}))=\log(27) \\ (a_n)^{a_n}=27=3^3 \implies a_n = 3$ Bonus Because of the function we just made, we have proven that there is no initial value such that the limit as n approaches infinity is infinity. Therefore, the only way the limit could not exist is if the number eventually gets negative or when the value oscillates between 2 fixed values. So in other words $a_1=a_3=\frac{\log(27)}{\log(n)}=\frac{\log(27)}{\log(\frac{\log(27)}{\log(\frac{\log(27)}{\log(n)})})}$ and $a_0=a_2=n=\frac{\log(27)}{\log(\frac{\log(27)}{\log(n)})}$ . Let's just solve for one equation and make sure that the other is not equal. So, to make it simple, let's solve for the second case: $n=\frac{\log(27)}{\log(\frac{\log(27)}{\log(n)})}\\ \log(\frac{\log(27)}{\log(n)})\cdot n = \log(27) \\ \log((\frac{\log(27)}{\log(n)})^n)=\log(27) \\ (\frac{\log(27)}{\log(n)})^n= 27 \\ \frac{1}{(\log(n))^n}=\frac{27}{(\log(27))^n} \\ (\log(n))^n=\frac{(\log(27))^n}{27} \\ n \approx 1.29543 \textrm{ or } 12.73327$ Upon inspection, it is clear that the number becomes negative if it is not between these two numbers, so this means that the interval on which $a_0$ can exist is $a_0 \in (1.29543, 12.73327)$

The plot of $a_n$ against $n$ shows the convergence clearly.

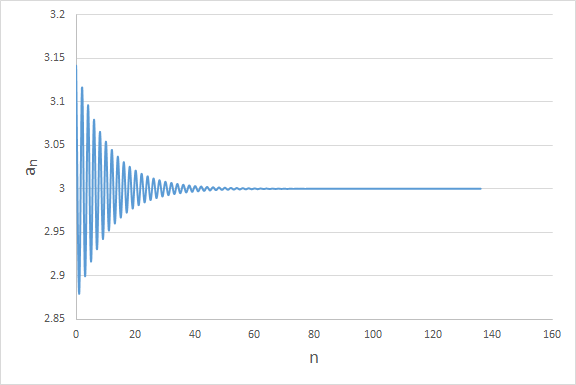
As mentioned by @Chan Lye Lee , $a_n = \log_{a_{n-1}} 27$ , $\implies a_{n-1}^{a_n} = 27 = 3^3$ . If $\lim_{n \to \infty} a_n$ exists, then $\lim_{n \to \infty} a_n$ = $\lim_{n \to \infty} a_{n-1} = \boxed{3}$

Bonus: We note from the graph that the values of $a_n$ oscillate up and down. The limit does not exist when $a_n$ oscillates between two values $a_0$ and $a_1$ . This happens when $a_0^{a_1} = a_1^{a_0} = 27$ . Let these two values be $\alpha$ and $\beta$ , then the limit exist if $\alpha < a_0 < \beta$ and it is found that $\alpha \approx 1.29543$ and $\beta \approx 12.73327$ . Note that $\alpha^\beta = \beta^\alpha = 27$ .

$a = \log _{\log _{\log _{...} 27} 27} 27$

$a = \log _{a} 27$

$a^a = 27$

$a = 3$

The first question one should ask is: What about $\pi$ is important in this problem? In this case, it is a property that $\pi$ has been known to have for thousands of years. A fundamental theorem everyone should know, that $\pi > 3$ . So how can we apply this? Well, notice that $27 = 3^3$ so $\log_3 27 = 3$ and therefore $a_1 = \log_{\pi} 27 < 3$ . But now that $a_1 < 3$ this implies that $a_2 = \log_{a_1} 27 > 3$ . So we have the general property that $a_{2n} > 3$ and $a_{2n+1} < 3$ . Now, we know that the limit exists so let's try to conjecture where that limit must be. If the limit is bigger than 3 then that would be contradictory as the $a_{2n+1}$ would never converge to a number bigger than 3. If the limit was smaller than 3 then that would be contradictory as the $a_{2n}$ would never converge to something smaller than 3. But we know the limit exists so it must be exactly $3$ .

My solution was: When you're lazy on a Sunday night, type '1, 2, and 3' into the answer box. Looks like I was correct.

Easy, just use an iterative method starting with π as the base of the logarithm