Infinite Series - 2
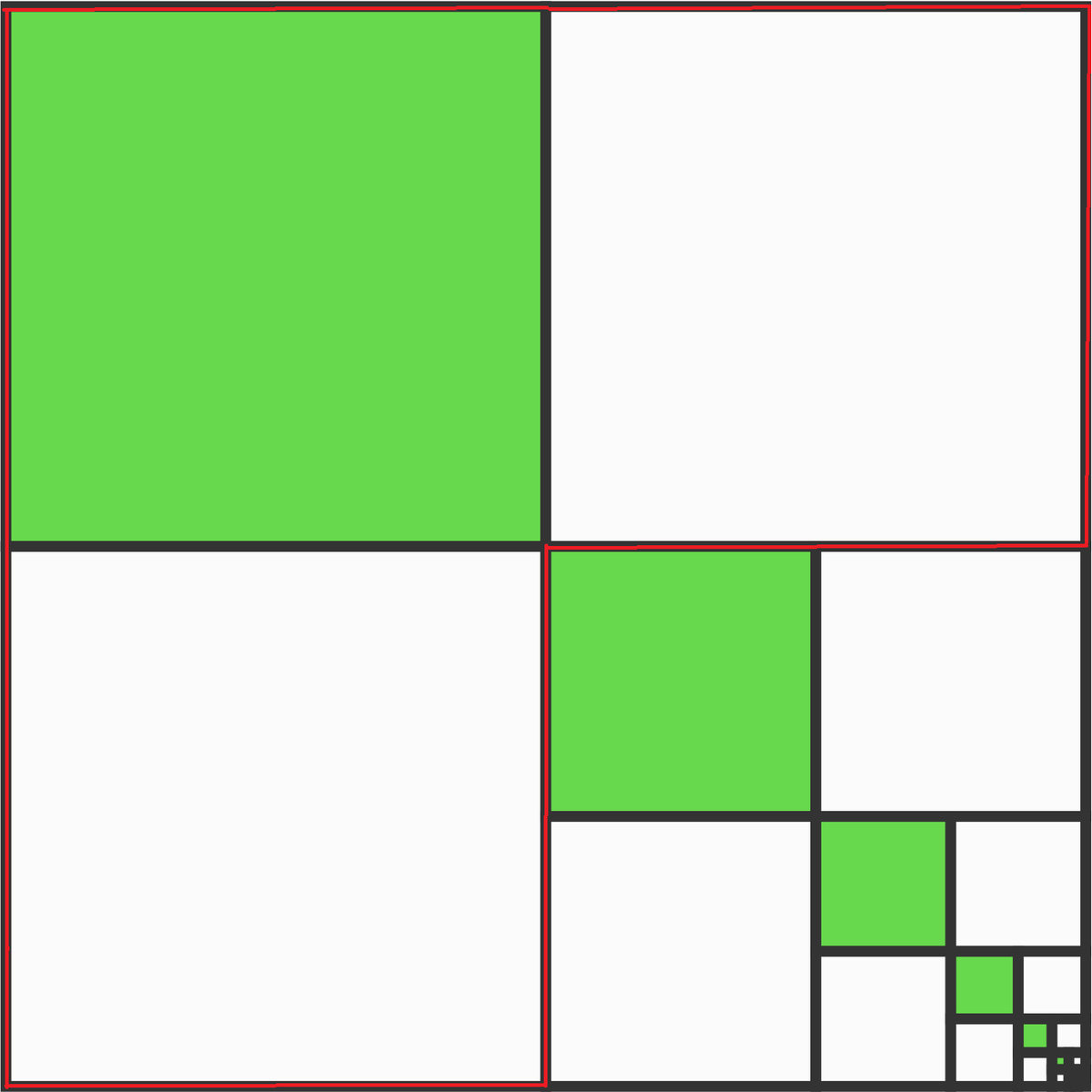
Every green square is one quarter of the square it's inscribed in.
If the pattern continues infinitely, what fraction of the total figure will be green?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
27 solutions
Moderator note:
If you liked this problem, note that in our Out of the Box Geometry course we have a whole section on infinite arithmetic. It is possible to justify the general formula for a sum of geometric series purely through geometry.
To expand this as a series, the green area is (1/3) (3/4) + (1/3) (3/16) + (1/3)*(3/64) + ... = (1/3)
It says outermost "square", which is why I'm confused that the L shape is highlighted. Is the wording wrong? Or am I missing something?
Log in to reply
If you divide the square into infintely many L shapes, you'll see that every green square is 1/3 of the L-shape it's in. Using some common sense, you'll get 1/3. The wording isn't wrong, you just can't see the perspective.
Yes, diagram is misleading. Perhaps staff could align their descriptions better with their diagrams.
This is correct, isn't it? Used the same exact logic and got that answer.
I added up the areas of the first few squares in this sequence and realised pretty quickly that the sum was closing in on 1/3 (by the time you have added the green square that is 1/256 of the area of the original big square to the existing sum the combined areas of the green squares is 85/256).
1 2 3 4 |
|
1 |
|
nice visual explanation. cool!
Beautiful!
elegant.... how might this visual helps students 'construct' the geometric progression formula? would love to know.... but out of all the solutions, i love how this one connects to the core concept of fraction. Thank you!
Just redefine the question. Simple. If you would state: one third is green, no matter how small the area. If you added up all the areas, how much would be green?
I guess I don't understand the question. It says "Every green square is one-quarter of the square it's inscribed in." So we're talking about a square that's split into 4 equal parts and one of the parts is green. That's one-quarter. The question does not say you need to account for the 4th (bottom-right section) that is also split into 4 section in an infinite pattern. I see how including the infinite pattern accounts for the solution given, but the first statement doesn't imply it. It only says every green square is one-quarter of the square it's inscribed in, which to me, means we are to ignore the bottom right quadrant in that sentence. The picture makes sense. The qualifying statement and following question doesn't.
Log in to reply
The only reason for the opening statement is for people to know we are dealing with exactly one-quarter; otherwise it'd be left out.
"the pattern continues infinitely" refers to the image.
Nice Brilliently asked question and a cool answer
Respected Sir and everyone , Please excuse me for posting this comment . Rather than saying that this is a comment this a burning issue in my heart . Please take it seriously .
I have a dream getting 100 or more up votes for an individual solution . I wrote a solution for the question water shadows (which is adjacent to this question) 6 days ago (on 21 April) . When I wrote the solution I thought it is a good one and will definitely accomplish my dream .
I am extremely happy when I saw that the question is in one of the problems of the week . I thought I am nearer to my dream because nobody posted any solution at that time expect me to this question and my solution is a clear and good one . But after these four days I am extremely sad because even more than 11,000 people solved that question only 83 people are discussing solutions . As a result at present I am only left now with 45 up votes . Although my solution deserves more than 100 up votes due silly reasons it is unable to accomplish my dream .
At first when I solved this question (infinite squares) on Monday morning I solved in the manner you did . I thought to post the solution but when I saw you have already posted the same solution (and now you got 299 up votes) . But I didn't worry at that time because I had hope that my solution to water shadows question will definitely cross 100 up votes .
Once see the up votes to the top solutions for the 5 questions of the problems of this week and see how odd it looks :
Infinite squares - Jason Dyer - 349 up votes
Water shadows - Ram Mohith - 57 up votes (see how odd it looks)
Third problem - Zain Majumder - 167 up votes
Fourth problem - Jeremy Galvagni - 129 up votes
Fifth problem - Micheal Mendrin - 250 upvotes
My point is that please try to discuss solutions to every question you solved and try to up vote the solution you admire as much as possible . If you do that many people like me will acheive what they deserve .
Please try to understand my problem .
Take a look at the L shape at the beginning. 1/3 of the shape is haded in green. If the pattern continues repeatedly, the green shading will always take up 1/3 of the total shape. To get to this conclusion, I drew the L shape diagram. To achieve the answer differently, I would try to look at the squares, since they are all the same size, it's pretty obvious that the green will take 1/3 of the shape. I would rate this problem a 1 because it was quite easy to solve. While solving it, I felt pretty confident about it.
Let the area of the original be 1. Then the area of first green square is 4 1 , that of second green square is 4 1 × 4 1 , the third, 4 1 × 4 1 × 4 1 and so on. Then the total green area is given by:
A green = 4 1 + 4 2 1 + 4 3 1 + ⋯ = 4 1 ( 1 + 4 1 + 4 2 1 + 4 3 1 + ⋯ ) = 4 1 ( 1 − 4 1 1 ) = 3 1 Sum of geometric progression (see note).
Note: Sum of geometric progression .
S n r S n S n − r S n ⟹ S n ⟹ S ∞ = 1 + r + r 2 + r 3 + ⋯ + r n = r + r 2 + r 3 + r 4 ⋯ + r n + 1 = 1 − r n + 1 = 1 − r 1 − r n + 1 = n → ∞ lim 1 − r 1 − r n + 1 = 1 − r 1 for ∣ r ∣ < 1
Could you explain the third step of simplification pls?
Log in to reply
Sum of geometric progression is given by k = 0 ∑ n r k = 1 − r 1 − r n + 1 . For n → ∞ , n → ∞ lim k = 0 ∑ n r k = 1 − r 1 for ∣ r ∣ < 1 .
Third step could be this way: A=1/4 * (1+A) and then a little algebraic magic: 4A=1+A A= 1/3 What I don't know: how to use Latex. (with an Android smart phone)
I have added a note to explain it. Check the wiki also.
hey can you explain the third step in a less complex way?
Log in to reply
I have added a note to explain. Check the wiki also.
Look for proofq about geometric series
Log in to reply
I have added a note to prove it. Check the wiki also.
Another way to express that would be:
A = 1/4 +1/(4^2) + 1/(4^3) + ...
=1/4*(1+1/4 +1/(4^2) + 1/(4^3) + ...)
=1/4*(1+A)
4A = 1+A
3A = 1
A = 1/3
Log in to reply
This is brilliant, so simple it makes me feel stupid! Please post this as a separate solution instead of as a comment here
Respected Sir and everyone , Please excuse me for posting this comment . Rather than saying that this is a comment this a burning issue in my heart . Please take it seriously .
Note : This post is regarding the Easy section of this problems of week .
I have a dream getting 100 or more up votes for an individual solution . I wrote a solution for the question water shadows (which is adjacent to this question) 6 days ago (on 21 April) . When I wrote the solution I thought it is a good one and will definitely accomplish my dream .
I am extremely happy when I saw that the question is in one of the problems of the week . I thought I am nearer to my dream because nobody posted any solution at that time expect me to this question and my solution is a clear and good one . But after these four days I am extremely sad because even more than 11,000 people solved that question only 83 people are discussing solutions . As a result at present I am only left now with 45 up votes . Although my solution deserves more than 100 up votes due silly reasons it is unable to accomplish my dream .
At first when I solved this question (infinite squares) on Monday morning I solved in the manner you did . I thought to post the solution but when I saw you have already posted the same solution (and now you got 299 up votes) . But I didn't worry at that time because I had hope that my solution to water shadows question will definitely cross 100 up votes .
Once see the up votes to the top solutions for the 5 questions of the problems of this week and see how odd it looks :
Infinite squares - Jason Dyer - 349 up votes
Water shadows - Ram Mohith - 57 up votes (see how odd it looks)
Third problem - Zain Majumder - 167 up votes
Fourth problem - Jeremy Galvagni - 129 up votes
Fifth problem - Micheal Mendrin - 250 upvotes
My point is that please try to discuss solutions to every question you solved and try to up vote the solution you admire as much as possible . If you do that many people like me will acheive what they deserve .
Please try to understand my problem .
Log in to reply
Have you reposted the problem after you have provided the solution? It would help other members attracted to the problem. I think members are up voting solutions they like or else how solutions get all the up votes. Do you use LaTex properly? I see that you leave a space before commas and periods (full-stops) consistently, which Microsoft Word marks them grammatically wrong.
Log in to reply
Thanks. I will look after the commas and full stops.
But the main point is that only 107 people are discussing the solution. If you want you can check how many people are discussing to each problem in this problems of the week.
Log in to reply
@Ram Mohith – It takes time. I have written (Solutions - 4955 total, ~34K upvotes). Was once voted as best solution writer with Brian Charlesworth in BSWC . I posted the solution before this problem is selected as weekly problem.
Log in to reply
@Chew-Seong Cheong – Ok. Thanks for you guidelines
Actually I am not worrying about my up votes . I am saying that people who deserve more up votes are not achieving that because less number of people are discussing the solutions .
Simple,
Green Area: 0 . 2 5 + 0 . 2 5 ∗ 0 . 2 5 + 0 . 2 5 ∗ 0 . 2 5 ∗ 0 . 2 5 + . . .
(It's a geometric progression with first term ( a ) 0 . 2 5 and common ratio ( r ) 0 . 2 5 , the infinite sum is given by 1 − r a )
Answer : 1 − 0 . 2 5 0 . 2 5 = 0 . 7 5 0 . 2 5 = 3 1
:)
Yeah a pretty simple way of solving it
Log in to reply
True, it's a straightforward problem...:)
Log in to reply
Could you solve this problem without explicitly knowing the geometric progression? I think that’s the hang up for most ppl on this problem...
Log in to reply
@Korey Hayes – Yes, the first solution by Jason does solve without using G. P. Let me know if you need any clarification...
Agree that it is somewhat simple to realize the first part. To me it was difficult to go on from there and see what that progression would converge to, not being familiar with geometric progressions in general.
If the fraction of the square that is green is f , then by considering each quarter of the square, we write down an equation: f = 4 1 + 4 f . This is because the top-right quarter is green, and the same fraction of the bottom-right quarter is green as the fraction of the whole square that is green.
Therefore, by multiplying by 4, 4 f = 1 + f , so 3 f = 1 , and we have that f = 3 1 .
waoo nice method..🤗🤗
Since the first green rectangle is a quarter of the hole/1 we can write its area as
4
1
, the term for the next square is a quarter of a quarter so
4
1
x
4
1
which is
4
1
to the power of 2, the third will be
4
1
to the power of 3 the fourth
4
1
to the power of 4 and so on.. (my images are different but the problem works the same)

We can write the series of numbers as:
 If we move the green rectangles one step down/right in my example this happens:
If we move the green rectangles one step down/right in my example this happens:
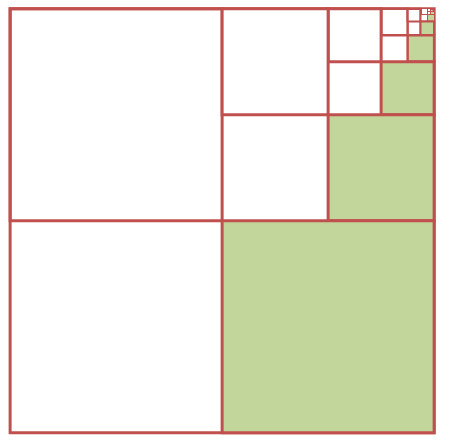 Now we can see that the green rectangles are lining up perfectly with one set of the unoccupied white squares. We can also perform a vertical translation of the green squares from their original position, to fill the other set of white squares:
Now we can see that the green rectangles are lining up perfectly with one set of the unoccupied white squares. We can also perform a vertical translation of the green squares from their original position, to fill the other set of white squares:
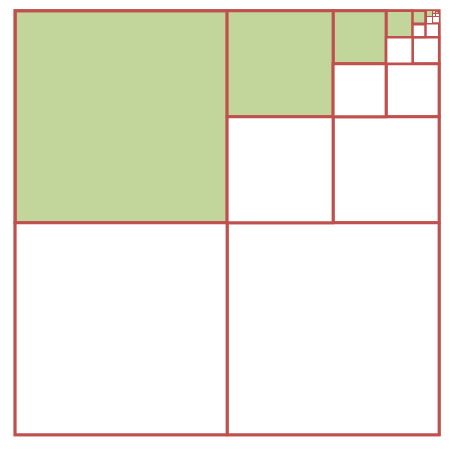 Since shifting doesn't change the area of the squares, we can see that by performing both shifts, we can fill the unit square completely with three copies of our series:
Since shifting doesn't change the area of the squares, we can see that by performing both shifts, we can fill the unit square completely with three copies of our series:
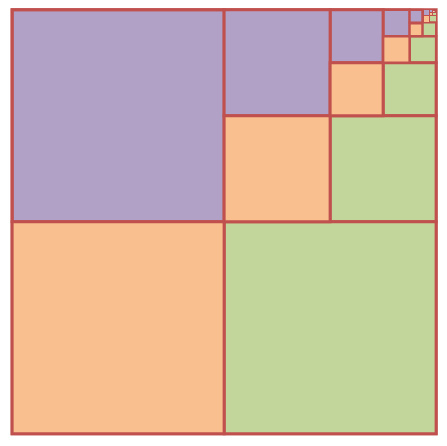 Thus we can see that the area of the original green rectangles were exactly equal to
3
1
Thus we can see that the area of the original green rectangles were exactly equal to
3
1
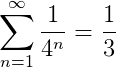 I didn't come up with this solution but I think its a nice way of visually confirming the answer without using any complicated algebra, I wouldn't answer this on a test though :)
I didn't come up with this solution but I think its a nice way of visually confirming the answer without using any complicated algebra, I wouldn't answer this on a test though :)
Each green square is placed between two white squares of equal area . So out of three squares two are white and one is green . This series goes on continuously till infinity .
Therefore , 3 1 of the outer square will be green .
I just figured it had to be the fraction that, when written out in decimals, just kept repeating forever. Does that make sense? And that only works because this was a multiple choice question.
That's how I did it too, having never learned the formula for an infinite progression as noted in an answer above. I could learn a lot from this app!
That's smart.
There’s a nice illustration of this sequence in the Number Theory course, chapter: Exploring Infinity that clearly illustrates that the series approaches 1/3 ...
Some of the solutions have used the general formula for finding the limit of this type of series. For the benefit of those who are not familiar with it here is a rough derivation:
Let x = r + r 2 + r 3 + ⋯ Notice that if you (a) multiply the series by r or (b) subtract r from the series you obtain the same result:
(a) r x = r 2 + r 3 + r 4 + ⋯ (b) x − r = r 2 + r 3 + r 4 + ⋯
Thus r x and x − r are equal, giving a simple equation that can be rearranged to give a general solution for x : r x = x − r x − r x = r x ( 1 − r ) = r Formula x = 1 − r r
Let the area of the original be 1. The first green square's area is 4 1 , the second green square's area is 4 2 1 , the third green square's area is 4 3 1 , and so on. So the total green area, represented by x is:
x = 4 1 + 4 2 1 + 4 3 1 … = 4 1 ( 1 + 4 1 + 4 2 1 + 4 3 1 … ) = 4 1 ( 1 + x )
Since we have x = 4 1 ( 1 + x ) , we can solve for x :
x = 4 1 ( 1 + x ) ⇒ 4 x = 1 + x ⇒ 3 x = 1 ⇒ x = 3 1
Therefore, the answer is 3 1 .
Using intuitive thought, I remembered that between all the solutions given to me, only 1/3 continues to have a "repetitive" pattern (i.e. 0.33333...), while 1/4, 3/8, and 2/5 are non-repeating decimals. Using this thought I concluded that the solution was 1/3 due to its infinite nature.
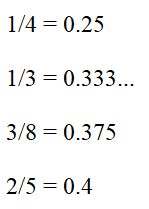
Good thinking . You deserve up votes
Let the area of the biggest square be equal to 1 . Then, we can write the green area S as the sum :
S = 4 1 + 1 6 1 + 6 4 1 + …
By putting 4 1 in evidence, we obtain :
S = 4 1 ( 1 + 4 1 + 1 6 1 + … )
Recognizing the original sum S in the parentheses, we can rewrite this last equation as :
S = 4 1 ( 1 + S )
and solve it for S :
S = 4 1 ( 1 + S ) ⇒ 4 S 3 S S = 1 + S = 1 = 3 1 ■
4 1 + 4 2 1 + 4 3 1 + . . . = 4 1 ( 1 + 4 1 + 4 2 1 + . . . ) = 4 1 ( 1 − 4 1 1 ) = 4 − 1 1 = 3 1
1/A + (1/A)^2 + (1/A)^3 ... (1/A)^n = [ 1-(1/A)^n ]÷(A-1)
You can check the above equation.
In this case n = infinite and A = 4 So the answer is 1÷(4-1) = 1/3
I just looked at the outermost square and it's 3/1
It only took less than a minute
either I did it to chance or did it with the right method
The Green area is in Geometric infinite series. Let the total green area equal 'S'. Then 4 1 + 4 2 1 + 4 3 1 + 4 4 1 + ⋯ = S Hence, S= 1 − 4 1 4 1 = 4 3 4 1 = 3 1
απλώς κάνοντας πράξεις το άθροισμα τείνει στο 0.33 (1/4+1/16+1/64+...)
The shape is self replicating: The green area of the whole shape is equal to the green quarter square (top left) plus one fourth of itself (bottom right).
This gives us:
A = 1/4 + A/4
Which simplifies down to:
A = 1/3
Working out the first 3 squares is enough. 0.25 + 0.0625 + 0.015625 = 0.328125 ; progression will never reach 0.4 (2/5) so answer must be 1/3.
x = 1/4 + 1/4(1/4) + 1/4(1/4)(1/4) ... 4x = 1 + x 4=1/3
think of a fractal .. the fraction of area of the inner square is the same as the fraction of the whole
f = 1/4 + f•(1/4)
subtract f•(1/4) .. 3f/4 = 1/4
multiply through by 4 .. 3f = 1
divide by 3 .. f = 1/3
n = 1 ∑ ∞ 4 n 1 = 3 1
But this works on TI-84 calcs
1 2 3 |
|
Infinite geometric sequence
S= A/(1-r) S=sum A= initial r= ration between - 1 to 1 exclusive
Answer is 1/3
The other three options are rational numbers.
emm....I just drew a little precisely and by looking at it, I can tell the area is between 1/4 and 3/8, so it must be 1/3
Suppose the area of the largest square is a^2. then, first green square is 1/4 (a^2), second green square is 1/4 ((a/2)^2 and so on. total = (1/4+1/16+1/64+.....inf) (a^2) =(1/4)/(1-1/4) a^2 = 1/3
1/4 + 1/16 + 1/64 + 1/256 = 0.33... = 1/3.
The figure consists of an infinite number of similar "L" shapes; one of them is marked above. In each "L", there are three congruent squares, one which is shaded green. Therefore the area that is green is 3 1 of the entire figure.