A calculus problem by Kunal Gupta
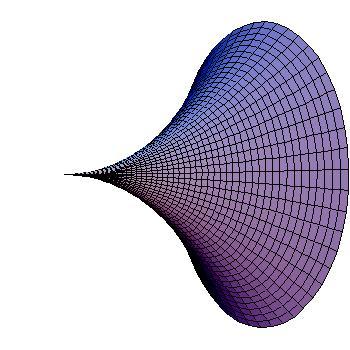Consider the curve
in the first quadrant. Now it's rotated about the
to obtain a solid of revolution. What is its surface area to 4 decimal places?
The answer is 7.2118.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Using the Formula for Surface Area: \[\begin{array}{} \text{ Area } & =\displaystyle \int _{ a }^{ b }{ 2\pi f(x)\sqrt { 1+{ (f'(x)) }^{ 2 } } \text{dx }} \\ & = \displaystyle \int _{ 0 }^{ \infty }{ 2\pi { e }^{ -x }\sqrt { 1+{ e }^{ -2x } } \text{dx} } \\ & =\pi \sqrt { 2 } +\pi \log \left[ 1+\sqrt { 2 } \right] \\ & \approx 7.2118 .\square \end{array} \]