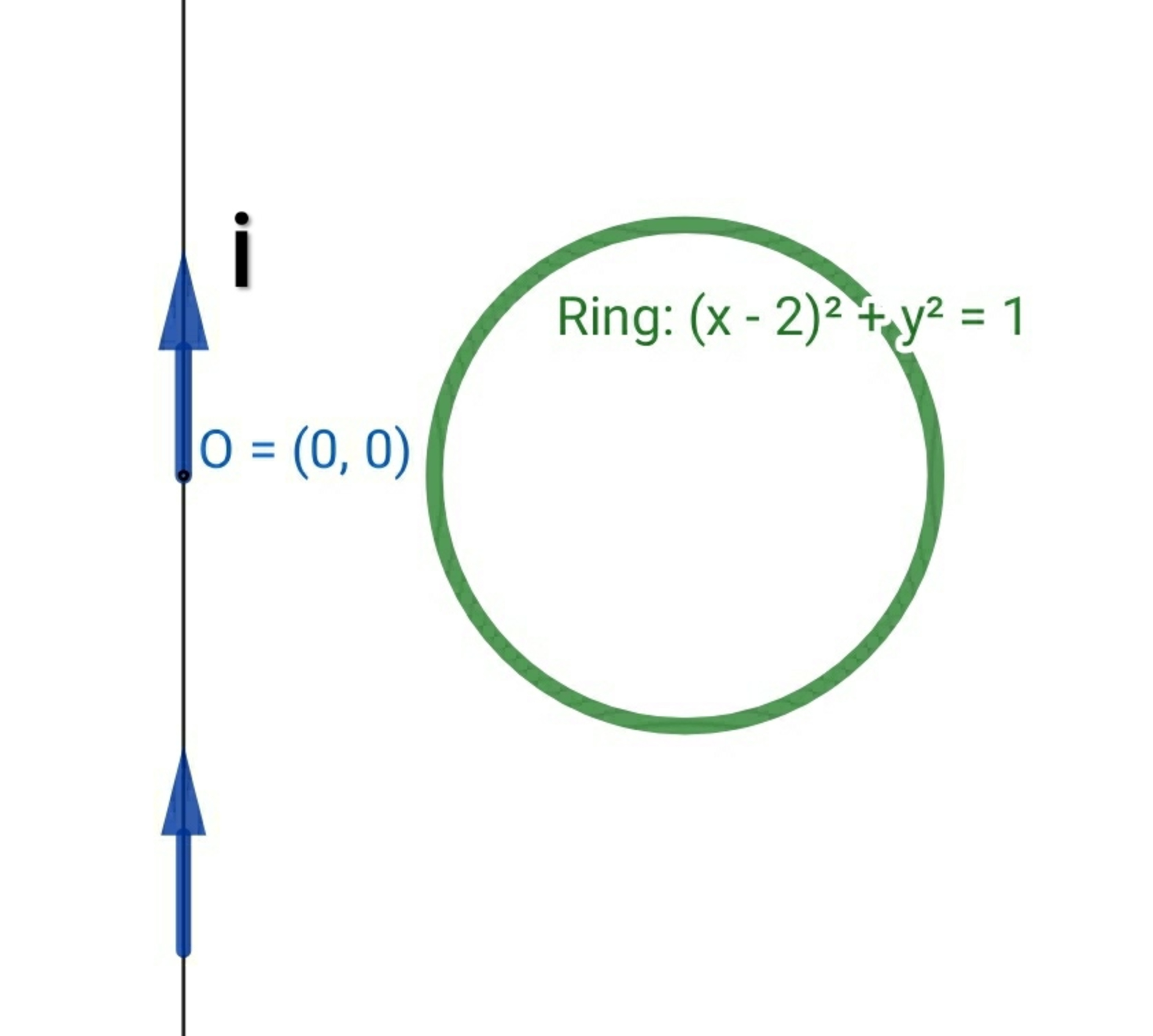
Infinite Wire with Sinusoidal Current
A infinitely long current carrying wire placed in
x
=
0
,in
x
y
plane
i
=
i
0
s
i
n
(
ω
t
)
.A circular ring of resistance
r
, parallel to
x
y
plane is located at
(
x
−
2
)
2
+
y
2
=
1
,
z
=
0
.
 Find
i
(
t
)
in the ring
Find
i
(
t
)
in the ring
Answer comes in the form of
i
(
t
)
=
μ
0
i
0
r
(
α
−
β
)
ω
cos
(
ω
t
)
Type your answer as
α
+
β
=
?
Bonus
1)
If electric field is generated,then calculate it also.
2)
Don't forget point
1
of bonus.
The problem is original.
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
@Alak Bhattacharya What about electric field? Please sir
Log in to reply
you should mention in the problem statement to ignore the magnetic field produced by the circular loop. also biot savart law is only an approximation for currents that change slowly with time, aka approximately magnetostatic. for an exact solution, use jefimenko's equations.
Log in to reply
Where arises the problem while applying Biot-Savart's law in the case of a time varying current?
Log in to reply
@A Former Brilliant Member – biot savart law does not take into account the magnetic field produced by a time varying electric field.
E = 2 π ( 2 − 3 ) μ 0 i 0 ω cos ω t .
Log in to reply
this is not correct. the electric field on the circular loop that is nearer to the infinite wire is stronger than the electric field on the farther side. you will see this if you use the differential form of faraday's law.
Log in to reply
@Ramon Vicente Marquez – It is curl of induced electric field that varies with the distance of the point where it is calculated from the current carrying wire. Integral form of any law gives an overall magnitude, not a particular magnitude at a point.
Log in to reply
@A Former Brilliant Member – well yes the E that you calculated is the "average" along the circular loop. but i would like to emphasize that the E actually varies at different points of the loop.
Log in to reply
@Ramon Vicente Marquez – @Ramon Vicente Marquez can you find E as a function of θ in the loop??
Log in to reply
@A Former Brilliant Member – how about finding E as a function of the distance from the infinite wire? what if we included the effect of time varying electric field? what if we consider the fields produced by the circular loop? the problem you posted is actually quite complicated, so make sure to state all assumptions.
@Ramon Vicente Marquez I am listening it for the first time Jefimemko's equation.
Φ m a g = π μ 0 i ∫ 1 3 x 1 − ( x − 2 ) 2 d x = μ 0 i ( 2 − 3 ) ⟹
induced e. m. f. = − d t d Φ m a g = ( 2 − 3 ) μ 0 d t d i = ( 2 − 3 ) μ 0 i 0 ω cos ω t ⟹
current through the ring is r ( 2 − 3 ) μ 0 i 0 ω cos ω t .
So, α = 2 , β = 3 and α + β = 5 .