Infinity is lovely
K = 5 + 5 − 5 + 5 − 5 + …
If K can be expressed in simplest form as c a + b , where a , b , c are positive integers, find the value of a 2 + b 2 + c 2 .
The answer is 294.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Nice solution,it avoids something like x^4...
Log in to reply
True, but if you use the "x^4 approach" you get to practice your skills in factorizing polynomials. Still, i love this solution
I saw this method stack exchange and used it to great effect on two nested radical problems. Thank you, sir. :)
Nice solution buddy up upvoted it
I've definitely seen it before...
Umm......
See the answer comes as c a + b and you are asking a 2 + b 2 + c 2 but in your solution , it says b = 1 7 but according to c a + b , b = 1 7 .
Please look over my problem.
Log in to reply
Im really sorry, the real problem said "is at the form (a+b)/c" but brilliant edited this.
Ya i also confirmed it by wolfram alpha
Log in to reply
Now i fixed this!, brilliant edited this c a + b to this! c a + b im really sorry for the trouble, but brilliant did a bad-edition.
ok,we don't talk about the problem ,I wonder how u recognized 「(x²-x-4)(x²+x-5)」?I finally ask Wolfram.
Log in to reply
This is my method.
x 4 − 1 0 x 2 + x + 2 0 = 0
4 x 4 − 4 0 x 2 + 4 x + 8 0 = 0
4 x 4 − 3 6 x 2 + 8 1 = 4 x 2 − 4 x + 1
( 2 x 2 − 9 ) 2 = ( 2 x − 1 ) 2
( 2 x 2 − 9 ) 2 − ( 2 x − 1 ) 2 = 0
( 2 x 2 + 2 x − 1 0 ) ( 2 x 2 − 2 x − 8 ) = 0
( x 2 + x − 5 ) ( x 2 − x − 4 ) = 0
This how i recognized the factors:- f a c t o r s o f t h e a b o v e p o l y n o m i a l c a n b e o f t h e f o r m : − ( a k 2 + b k 1 + c ) ( a ′ k 2 + b ′ k 1 + c ′ ) _ _ _ _ ( 1 ) N o w c o e f f i c i e n t o f k 4 i s 1 s o a = a ′ = 1 a l s o c o e f f i c e i n t o f k 3 i s 0 s o b = 1 a n d b ′ = − 1 N o w s u b s t i t u t i n g a , b , a ′ , b ′ a n d e x p a n d i n g ( 1 ) w e g e t k 4 − k 2 ( c + c ′ + 1 ) + k ( c − c ′ ) + c c ′ c o m p a r i n g i t w i t h t h e o r i g i n a l p o l y n o m i a l w e g e t c = 5 a n d c ′ = 4 s o t h e f a c t o r s a r e ( k 2 + k − 5 ) ( k 2 − k − 4 )
Log in to reply
How do you know that b,b' = ±1 not ±2,±3,±4,... ???
Log in to reply
@Anuchit Thanasrisurbwong – Rishi's got the right idea, but it can be a bit more involved.
First, the possible rational zeros don't produce any zeros, so we can see if there are 2 quadratics that fit the bill. The coefficient of the k 4 term is 1, so that makes things a tad easier.
( k 2 + a k + b ) ( k 2 + c k + d ) = k 4 + ( a + c ) k 3 + ( a c + b + d ) k 2 + ( a d + b c ) k + b d
From this, we can match coefficients and get 4 equations. If they can be solved, then this is possible.
1) a + c = 0
2) a c + b + d = − 1 0
3) a d + b c = 1
4) b d = 2 0
Trying to solve them (at least for me) yields:
1) ⇒ c = − a
3) ⇒ a ( d − b ) = 1 ⇒ d − b = a 1
For this to work a 1 must be an integer, so a must be 1 or -1. Choosing either works (I chose 1)
1) a = 1 ⇒ c = − 1
3) ⇒ d = b + 1
4) ⇒ b ( b + 1 ) = 2 0 ⇒ b 2 + b − 2 0 = 0 ⇒ b = 4 , − 5
If b = 4 then d = 5 , but then equation 2 doesn't work. So:
4) b = − 5
3) ⇒ d = − 4
2) 1 ( − 1 ) − 4 − 5 = − 1 0 Check
Therefore, the assumption that a = 1 works and you are left with ( k 2 + k − 5 ) ( k 2 − k − 4 ) .
@Anuchit Thanasrisurbwong – see @louis w's solution.. you can easily notice that two get the simplest possible valuse of the unknowns it is important to keep b and b' unity. even if you change the values you will get the same values but a little more complex.
(K^2 - 5)^2 = 5 - K
K^4 - 10 K^2 + K + 20 = 0
K^4 + (u - 10) K^2 - u K^2 + K + 20 = 0
u^3 - 20 u^2 + 20 u - 1 = 0 is having 3 real roots but 1 simplest which is 1.
Therefore (K^2 - K - 4)(K^2 + K - 5) = 0
As we know that K = 2.56 approximately from the original expression,
K^2 - K - 4 = 0 is the one contains 2.56,
(K - 1/ 2)^2 = (1/ 2)^2 + 4 = 17/ 4
K = 1/ 2 +/- Sqrt (17) / 2 initially but not negative,
K = [1 + Sqrt (17)]/ 2 = 2.561552812808830274910704927987
1^2 + 2^2 + 17^2 = 294
K 2 = 5 + 5 − 5 + 5 − 5 + . . . .
K 2 − 5 = 5 − 5 + 5 − 5 + . . . .
( K 2 − 5 ) 2 = 5 − 5 + 5 − 5 + . . . . = 5 − K
K 4 − 1 0 K 2 + 2 5 = 5 − K → K 4 − 1 0 K 2 + K + 2 0 = 0
K 4 − 1 0 K 2 + K + 2 0 = 0 → ( K 2 − K − 4 ) ( K 2 + K − 5 ) = 0
Using the quadratic formula, we get the roots:
2 1 ± 1 7
2 − 1 ± 2 1
We choose the root with all positive numbers.
Moderator note:
Both 2 − 1 + 1 7 and 2 − 1 + 2 1 are positive numbers, how do you know which one is the right answer?
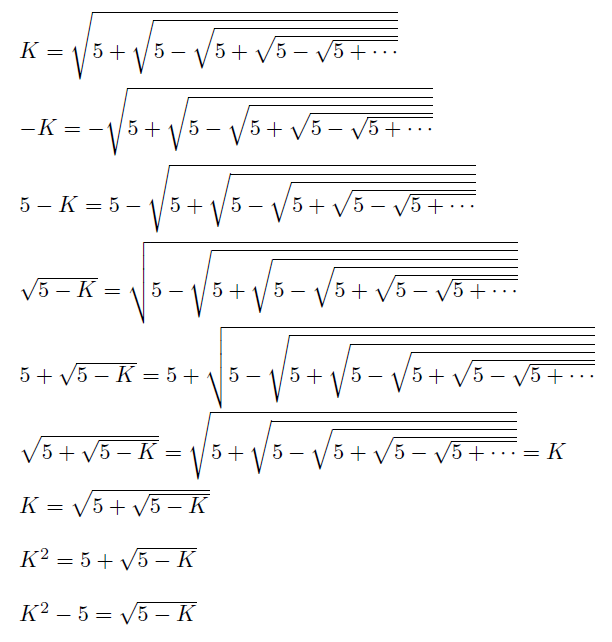
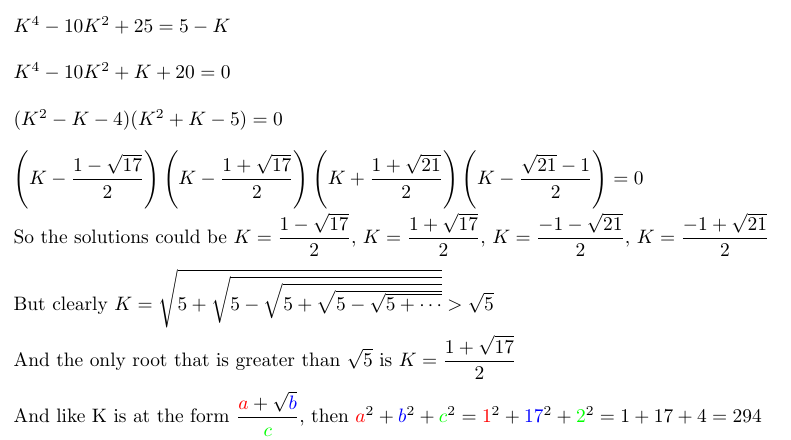
Another approach:
K = 5 + 5 − 5 + ⋯ L = 5 − 5 + 5 − ⋯
Then K = 5 + L and L = 5 − K . Square both equations: K 2 = 5 + L and L 2 = 5 − K and subtract them: K 2 − L 2 = K + L ⟹ ( K + L ) ( K − L ) = K + L . Since K + L = 0 : K − L = 1 ⟹ L = K − 1 .
Finally substitute that in the first equation:
K 2 = 5 + K − 1 ⟹ K 2 − K − 4 = 0
Using the quadratic formula we obtain, and with the fact that K > 0 :
K = 2 1 + 1 7
Comparing we get a = 1 , b = 1 7 and c = 2 . Hence the answer is 1 2 + 1 7 2 + 2 2 = 2 9 4 .