Insufficient Information On Areas?
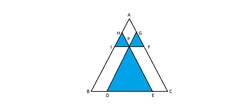 If P is a point inside the triangle ABC, and line segments DPG, HPE, FPI are drawn parallel to sides AB, AC and BC respectively through the point P. If area of triangles PDE, PFG and PHI are 36, 9 and 4 respectively, find the area of triangle ABC.
If P is a point inside the triangle ABC, and line segments DPG, HPE, FPI are drawn parallel to sides AB, AC and BC respectively through the point P. If area of triangles PDE, PFG and PHI are 36, 9 and 4 respectively, find the area of triangle ABC.
The answer is 121.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
This solution is better than the rest.
This question is very similar to a past AIME problem :)
Used the same method.
Note: Trianges PDE , PFG , PHI , and ABC are all proportional. Futhermore, the sum of the width of the inner triangles equals the width of ABC , and the sum of the height equals the height of ABC .
3 6 = 6 9 = 3 4 = 2 ( 6 + 3 + 2 ) 2 = 1 2 1
can u explain your reasoning behind the last two steps and why the sum of the heights
Log in to reply
I will try to explain with an example:
Suppose you have 3 similar right triangles with the given dimensions:
Triangle A has L =1, W =8, A =4. Triangle B has L =2, W =16, A =16. Triangle C has L =4, W =32, A =64. Then:
Between any two triangles, the ratio between each corresponding side is equal. Furthermore, that same ratio is also equal to the ratio between the squareroot of their area.
L B L A = W B W A = A B A A
You can further expand on this idea and we can say the ratio of corresponding sides of the sum of any two and the third are equal. The same is true for the squareroot of their area.
L C L A + L B = W C W A + W B = A C A A + A B
Now suppose, we didn't know anything about triangle C . If, I said the ratio between the sum of the lengths of A and B , and the length of C is 4 3 then we could solve the ratio to find L C .
L C 1 + 2 = 4 3 → 3 ⋅ L C = 4 ⋅ 3 → L C = 4
We can do the same with the widths and the squareroot of the areas.
W C 4 + 8 = 4 3 → W C = 1 6 A C 4 + 1 6 = 4 3 → A C = 8
Now to solve the problem you have to realize that segment IP = BD and segment PF = EC . This means that the sum of the widths of triangles PDE , PFG , and PHI is equal to the width of traingle ABC . In other words, the ratio between the sum of the widths of PDE , PFG , and PH , and the width of ABC is 1.
And, as I explained in the example, that same relation is going to be true for the squareroot of the areas. Therefore:
Area A B C 3 6 + 9 + 4 = 1 → Area A B C = 3 6 + 9 + 4
So we dont need to know the dimensions of the width or height of the triangles, using just the areas and the ratio, we found the squareroot of the area of ABC and thereby found the area.
Area A B C = ( 3 6 + 9 + 4 ) 2 = ( 6 + 3 + 2 ) 2 = 1 2 1
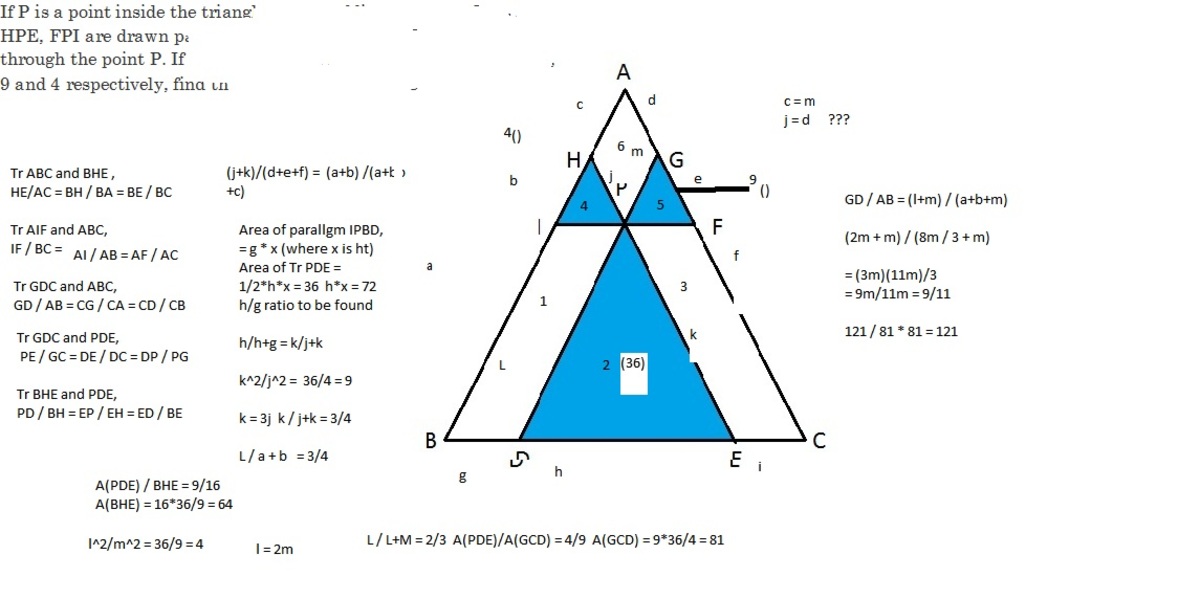 Labeling of sides, BI = a , IH = b, AH = c, AG = d, GF =e, FC = f, BD = g, DE=h, EC = i, PH = j, PE=k, PD = L PG = m
Labeling of sides, BI = a , IH = b, AH = c, AG = d, GF =e, FC = f, BD = g, DE=h, EC = i, PH = j, PE=k, PD = L PG = m
Gist of strategy : :
We first find ratio of corresponding sides of triangles PDE, HPI and PGF.
Then we move to finding ratio of corresponding sides of triangles PDE and BHE and PDE and GDC and then the rato of their areas and hence the areas of triangles BHE and `GDC (One of them will do).
Then we move from GDC to the triangle ABC ,try to find ratio of the sides and hence their areas and since we know A(GDC), we are done.
We consider similar triangles HPI and PDE..
Using the idea that areas of similar triangles are proportional to the squares of their corresponding sides , essentially A(PDE) / A(HPI) = k^2/j^2 = 36/4 = 9
Therefore, k=3j and k/(j+k) = 3/4
L/(a+b) = 3/4
Using the same principle of ratios of areas of similar triangles being proportional to square of corresponding sides, A(PDE) / A(BHE) = 9/16
A(BHE) = 16*36/9 = 64
Similarly L^2/m^2 = 36/9 = 4
Therefore L = 2m
L / (L + m) = 2/3
A(PDE)/A(GCD) = 4/9
A(GCD) = 9*36/4 = 81
Now, all we have to do is to connect A(GDC) to ABC
We We use the ratio GD/AB = (L+m) / (a+b+m) (l(AB) = a + b +c and c=m since they are opposite sides of a parallelogram). Alternatively, we could have considered triangle FAI and used the fact that DE/FI = PD/(AH+HI) and hence found AH / c. But that would be more work
Now, we know L=2m and L/(a+b) = 3/4
Therefore (a+b) = 4L / 3 = 4*2m / 3 = 8m / 3
GD / AB = (2m+m) / (8m/3 + m)
= 9/11
A(ABC) / A(GDC) = (11/9)^2 = 121 / 81
Therefore A(ABC) = 121/81 * A(GDC) = (121/81)*81
= 121
I felt a diagram would have been ideal and i had one ready but i could not find any means of attaching it to this post
Log in to reply
if you upload an image to image hosting site and insert the following code without quotations into you post you can attach an image:
" ![insert any caption here]{insert http address of image here} "
*Note: The caption inside the square brackets is not required. Only the web address inside the curly braces is required.
Log in to reply
testing ![this is a test]{http://www.revisionworld.co.uk/sites/revisionworld.com/files/imce/similar%20triangles.gif}
hrm, I guess it doesn't work in comments?
Log in to reply
@Skylar Saveland – my bad its not curly braces for the web address, its parentheses. It should show up in the preview if its works.
 this is a test
this is a test
Log in to reply
@Julio Reyes – How do i upload the images to the hosting site ? Do i send mail to brilliants ? I could always post something in one of the discussions group
Log in to reply
@Sundar R – image hosting is not done by Brilliant. They would have to be a third party website. I've been using postimage.org . You can upload your image there or any other image hosting site, and then copy the direct link to place inside the code to display the image.
Actually, there is 1 step that seems unnecessary in hindsight : Finding the area of the triangle BHE
Diagram should be there
Alternate Solution (without using the fact that l(AH) = l(PG) :(without using properties of parallelogram) :
Comparing Triangles AIF and PDE we know that l(DE) / l(IF) = l(DE) / [ l(IP) + l(PF) ] = 6/(2+3) = 6/5
We know that PD/(AH+IH) = 6/5 and we know that PD / IH = 2 and hence through property of similar triangles, PD/AH = 3 and AH = PG
The rest of the steps are similar to the above
Log in to reply
Sorry, there is a typo above. L(DE)/([l(IP) + I(PF)] = 6/(3+2) and not the other way since DE/IP = 3 Therefore PD/IH = PE/PH = k/j = 3 (from above explanation) and hence PD/AH = 2 (and this makes sense since AH = c = PG = m and PD = L = 2m in the explanation above.)
Since all the four triangles are similar, hence IP : DE : PF = 2 : 6 : 3
But, since IPBD and PFCE are parallelogramms, therefore, IP=BD and PF=EC
Thus, BD : DE : EC = 2 : 6 : 3 and BC= BD+DE+EC=11
Therefore, DE : BC = 6 : 11 and thus area=121*36/36 = 121
this one's more clear and more precise. it's just that BC <> 11. You could have just stated: If DE = 6x (for some x) then BC = BD+DE+EC = 11x making DE:BC=6:11
2 × A = 2 × 3 6 + 2 × 9 + 2 × 4
A = 1 2 1
Just an application of basic proportionality theorem
Shortest approach. Congratulations. +1)
3 6 = 6
9 = 3
4 = 2
6 + 3 + 2 = 1 1
1 1 2 = 1 2 1
Similar to my solution here: https://brilliant.org/community-problem/simple-cones/?group=XDaYBRWVrt5S
All 3 small triangles and the big triangle are similar. The ratio of their areas is the ratio of their side length, squared.
Log in to reply
You could improve this solution greatly by explaining the steps in words.
For example, you could say that P I : D E : P F = 2 : 6 : 3 , and hence B D : D E : E C = 2 : 6 : 3 . Thus B C : D E = 1 1 : 6 and hence by ratio of similar triangles, the area is 6 2 1 1 2 × ( 6 + 2 + 3 ) 2 .
Why do you add them and square it? I've seen that with a trapezoid before but why does it work?
As the 3 triangles are similars (because parallels sides), their ratio of areas are proportcional to the square ratio of sides. ( P F P I ) 2 = [ P G F ] [ P H I ] = 9 4 ∴ P F P I = 3 2 .
So, we can state P I = 2 k a n d P F = 3 k
With a similar argument, we can state D E = 6 k .
and, because the parallel lines, B D = P I = 2 k a n d E C = P F = 3 k
and so, B C = 2 k + 6 k + 3 k
Therefore, ( P I B C ) 2 = [ P H I ] [ A B C ] ⇒ ( 2 k 1 1 k ) 2 = 4 [ A B C ] ⇒ 4 1 2 1 = 4 [ A B C ]
[ A B C ] = 1 2 1