Ingenious Cat

Let us say the acceleration of cat is $a$ down the incline, the system of cat ladder would have same acceleration as mass of ladder is assumed $0$ . Component of acceleration in horizontal direction is $a \cos \alpha$ , and that in vertically downward direction is $a \sin \alpha$

Let $R_{1}$ be the reaction force at upper end and $R_{2}$ at lower end,

Apply Newton's Law on the system,

$R_{1} = ma \cos \alpha$ ,

$mg - R_{2} = ma \sin \alpha \Rightarrow R_{2} = m(g - a \sin \alpha)$

Say, cat has descended a distance $x$ .

Since rod is in static equilibrium, we can balance torque about any point on it, for convenience we choose the point at which cat is standing,hence , we get

$R_{2}(L-x) \cos \alpha = R_{1} x \sin \alpha$

$\Rightarrow m(g - a \sin \alpha)(L-x) \cos \alpha = xma \cos \alpha \sin \alpha$

$\Rightarrow a = \frac{g}{L \sin \alpha} (L-x)$

$\ddot t = -\frac{g}{L \sin \alpha} t$ ( $t = L-x$ )

This is equation of SHM and equilibrium position is $x=L$ , ( $t=0$ ) , hence time taken(from $t = L$ to $t = 0$ ) = $\frac{T_{shm}}{4}$

= $\frac{\pi}{2} \sqrt{\frac{L \sin \alpha}{g}} = \boxed{1.141s}$

The first thing in such problem is always to draw a force body diagram.

Lets make it for the plank. It is shown in the figure below:

where

$N_1$ is the normal reaction due to floor.

$N_2$ is the normal reaction due to wall.

$N_3$ is the normal reaction due to cat. Its magnitude is $mg\cos\alpha$

$f$ is the friction due to motion of cat. Since the friction on Cat acts in the upward direction along the plank, then due to Newton's third law, the friction on plank acts downward along the plank.

As the problem states that the plank is in rest so we balance the forces in x and y direction.

$\displaystyle \sum F_x=0 \Rightarrow f\cos\alpha+N_2=N_3\sin\alpha \,\,\, (*)$

$\displaystyle \sum F_y=0 \Rightarrow f\sin\alpha+N_3\cos\alpha = N_1 \,\,\, (**)$

We have three unknowns and only two equation. So we find the third equation by balancing the moments.

We balance moments about the lowermost point, that gives us:

$\displaystyle N_3(L-x)=N_2L\sin\alpha \Rightarrow N_2=\frac{N_3}{\sin\alpha}\left(1-\frac{x}{L}\right)$

where $x$ is the distance travelled by cat along the plank in time $t$ .

Substitute this in (*) to obtain $f$ ,

$\displaystyle \Rightarrow f=\frac{mg}{\sin\alpha}\left(\sin^2\alpha-1+\frac{x}{L}\right)$

Now apply Newton's second law on the cat. We get:

$\displaystyle mg\sin\alpha-f=m\ddot{x}$

Substitute $f$ and simplify to:

$\ddot{x}=\frac{g}{\sin\alpha}\left(1-\frac{x}{L}\right)$

Substitute $u=1-x/L \Rightarrow \ddot{x}=-L\ddot{u}$

Hence, we get:

$\displaystyle \ddot{u}=-\frac{g}{L\sin\alpha}u$

The solution of the above differential equation is $u(t)=A\sin(\omega t)+B\cos(\omega t)$ where $\omega=\sqrt{g/(L\sin\alpha)}$ .

The initial conditions are $u(0)=1$ and $\dot{u(0)}=0$ . From these initial conditions, we have $A=0$ and $B=1$ . Hence,

$\displaystyle u(t)=\cos(\omega t)$

When $x(t)=L$ we have $u(t)=0$ , $\Rightarrow 0=\cos(\omega t)$ . This gives

$\displaystyle t=\frac{\pi}{2\omega}=\frac{\pi}{2}\sqrt{\frac{L\sin\alpha}{g}}$

Substituting the values, $\boxed{t=1.143 \,\, \text{seconds}}$

Discovering such motion, I would say the cat is quite genius. :P

When I saw this problem for the first time I thought it was nearly impossible, then I started to think of how the forces were related to each other and how should be the force acting on the plank so the cat were able to descend it without losing contact.

The first thing I've done was draw all the forces acting on the plank in the simpler way: two normal forces exerted by the wall and by the floor and the interaction force between the cat and the plank. To determine the direction of the interacting force F I used a theorem called "Three-Force Theorem" here in Brazil, which is just saying that if a rigid body is subjected to forces acting at only three points the line of action of the three forces must be either concurrent or parallel.

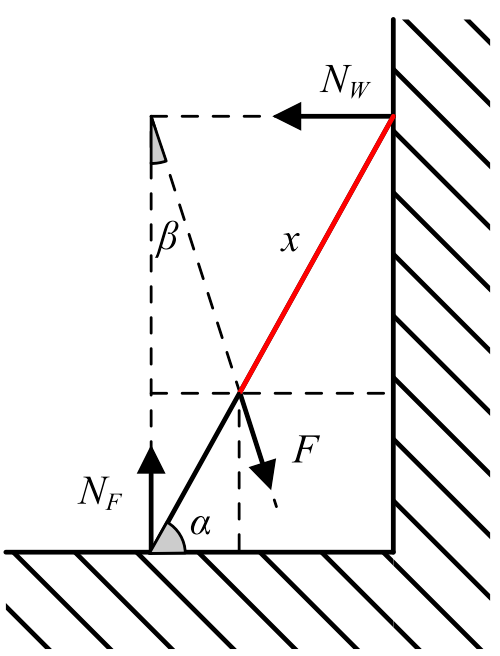Plank force diagram

The second thing I've done was draw a free-body diagram for the cat itself using the Newton's Third Law to represent the reaction of the interacting force with the plank:

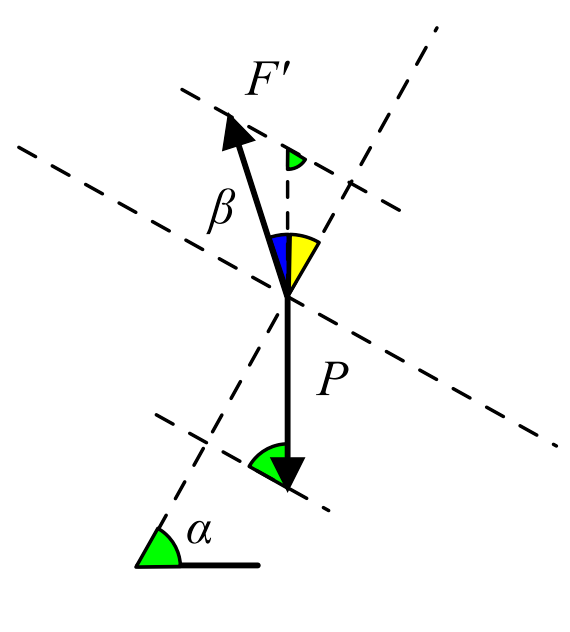Cat force diagram

From the first picture we can write the tangent of the angle $\beta$ as:

$\tan \beta = \left( \frac{L}{x} -1 \right) \frac{1}{\tan \alpha}$

Using the second diagram and the normal equilibrium of the cat with respect to the plank direction we can write:

$F \sin \left( \beta + \frac{\pi}{2} - \alpha \right) = P \cos \alpha$

Now in the plank direction itself there's net force:

$F_r = P \sin \alpha - F \cos \left( \beta + \frac{\pi}{2} - \alpha \right)$

Using the tree equations above and the Newton's Second Law:

$M a = M g \sin \alpha - M g \cos \left(\tan \left( \beta + \frac{\pi}{2} - \alpha \right) \right)^{-1}$

$\frac{a}{g} = \sin \alpha - \cos \alpha \left( \frac{\tan \alpha - \tan \beta}{1+ \tan \alpha \tan \beta} \right)$

$\frac{a}{g} = \sin \alpha - \cos \alpha \left( \frac{\tan \alpha - \left( \frac{L}{x} -1 \right) \frac{1}{\tan \alpha} }{1+ \tan \alpha \left( \frac{L}{x} -1 \right) \frac{1}{\tan \alpha} } \right)$

$\frac{a}{g} = \sin \alpha - \cos \alpha \tan \alpha \left( \frac{1-\left(\frac{L}{x}-1\right) \frac{1}{\tan^2 \alpha}}{\frac{L}{x}} \right)$

$\frac{a}{g} = \sin \alpha \left( 1- \frac{1-\left(\frac{L}{x}-1\right) \frac{1}{\tan^2 \alpha}}{\frac{L}{x}} \right)$

$\frac{a}{g} = \sin \alpha \left( \frac{\frac{L}{x}-1+\left(\frac{L}{x}-1\right) \frac{1}{\tan^2 \alpha}}{\frac{L}{x}} \right)$

$\frac{a}{g} = \sin \alpha \left(\frac{\left(\frac{L}{x}-1\right) \left( 1+\frac{1}{\tan^2 \alpha}\right)}{\frac{L}{x}} \right)$

$\frac{a}{g} = \sin \alpha \left( 1 - \frac{x}{L} \right) \left( \frac{1}{\sin^2 \alpha}\right)$

$\boxed{a = \frac{g}{\sin \alpha} \left( 1 - \frac{x}{L} \right) }$

Note that this acceleration is identical to the acceleration of a mass attached to a vertical spring hanging on the ceiling inside a gravitational field. For the analogy consider a mass m attached to a spring with constant k under a gravitational field G:

$ma = m G - k x$

$a = G - \frac{kx}{m}$

$a = G \left( 1 - \frac{x}{\frac{mG}{k}} \right)$

To go from the analogy to the problem itself its only needed to make the following substitutions:

$G \to \frac{g}{\sin \alpha}$

$\frac{m}{k} \to \frac{L \sin \alpha}{g}$

Now note that the time spent by the cat to go from $x= 0$ to $x = L$ is the same time spent by the mass to go from the initial position to the equilibrium position $x= 0$ to $x = \frac{mG}{k}$ . This time is equal a quarter of the total period of motion:

$t = \frac{T}{4}$

$T = 2\pi \sqrt{\frac{m}{k}}$

Using the second substitution:

$\boxed{ t = \frac{\pi}{2} \sqrt{\frac{L \sin \alpha}{g}} }$

$t = \boxed{1.14379\; s}$

*The jist of the problem is to identify how the cat makes the plank balance . as the cat moves down, the torque on the plank [about point of contact with the wall] due to normal by the cat on the plank changes. this change is nullified by the friction [between cat and plank] indirectly changing the normal of the ground on the plank changing its torque on the plank[ about point of contact with the vertical] *

. write the force equations and balance torque about point of contact with the vertical . obtain friction as a function between cat and plank of displacement of the cat{x} .write equation of motion then obtain velocity and finally time as a function of displacement by integrating and putting appropriate conditions on solving we get $\boxed{t=1.14seconds}$