Inscribe triangle
Triangle A B C is inscribed in a circle. The angle A B C is obtuse, and the altitude C H is tangent to the circle.
If H B = 1 0 and B A = 8 , what is the radius of the circle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Moderator note:
Briefly to note, as it came up a few times in the comments:
How you know the perpendicular bisector passes through the center of the circle?
Every point on the perpendicular bisector is equidistant from the endpoints of the chord. Since all radii are congruent and two radii connect the endpoints of the chord, the center of the circle is on the bisector.
Sorry I am new to this
How do you know that the perpendicular bisector of AB passes through the center of the circle?
Is it to do with the obtuse angle?
Log in to reply
The perpendicular bisector of a segment AB is, by its definition, composed of each points which are equidistant of A and B. So, if O the center of the circle passing by A and B, is not on the perpendicular bisector then OA is not equal to OB. Which is impossible. So O is on it.
The reason why in this case is true is because the triangle OAB is isoceles (OA=OB)
Oh I see now, I didn't Read the question right. Sorry
IMO, the perpendicular which starts from O and passes AB also passes the bisector of it (Because AB is a chord). You can easily prove this.
The only reason that the angle is specified as obtuse is to ensure H is to the left of B as in the diagram. If an acute angle is allowed, H would be to the right of B (and also A, given the lengths specified), and the radius would be 6 ( = 10 - 4) instead
I had no idea the perpendicular bisector of a chord passed through the center of the circle. Come to think of it it should be kind of obvious, but I can't explain why. Thanks for sharing the solution anyways.
Log in to reply
Ends of a chord are two points on the circle. Therefore the perpendicular bisector of a chord is every point which is equidistant from the two ends of a chord. Since the centre will form radii with both ends of the chord, it is equidistant, and on the perpendicular bisector
I think of it in the opposite way - the bisector of a chord from the circle's center must be perpendicular to it.
I did it the hard way, by relating two variables h=HC and r=OC through trigonometry. It produced 14 as the answer.
Log in to reply
Same. And after all the trigonometries I saw this solution...
How would you know the perpendicular bisector of AB passes through the center of the circle?
Log in to reply
Every point on a perpendicular bisector of a line segment is equidistant from the endpoints. In fact, the way to construct the center of a circle is to find the intersection of the PBs of two chords.
Alternatively, you can easily prove the bisector of AB from the center must be perpendicular to the chord pretty easily. (The two triangles formed are congruent because (a) one shared side, (b) bases formed by bisection are equal length, (c) third sides are both radii of the circle.)
My first posted problem of the week! My geometer's sketchpad picture was rather crummy (looks like my solution without rectangle lines) so I'm glad it was replaced.
Your solution lacks the main argument : The three perpendicular bisectors of a triangle's three sides intersect at the circumcenter (center of the circle which passes through all the vertices). Here by defintion the circumcenter is O. Therefore XB = 4.
I think you should add this : 'HBA is a straight line. '
Log in to reply
I think this is by the construction of H
It's the definition of the altitude of a triangle (look for the phrase "extended base").
Log in to reply
HC is the altitude of triangle CHB, but not necessarily of CHA. I agree that clarification would have been helpful.
Log in to reply
@Scott Rudell – Technically, H C is a side of CHB. HC (or as it's called, CH) is specifically called the altitude in the problem, of triangle ABC. Again, it's the definition of what an altitude of a triangle is.
I didn't realize that "inscribed in the circle" meant that all the sides of the triangle were chords of the circle. Much clearer, now. 😊
Nice! Its good to learn new concepts like perpendicular bisector. Another tool in my belt. I took me a moment to figure out why the perpendicular bisector passes through the center, but then I realized that it must be the case because AB is perpendicular to CH
Log in to reply
The perpendicular bisector of any chord passes through the center of the circle.
i still dont see how line BA is known to be parallel to HB. how do you know A has the same X axis as H?
Log in to reply
If it wasn't you would see the dotted line from the corner to B. Instead you see the line of the triangle, showing prefectly parallel lines.
It is so by definition. CH is the altitude of triangle ABC. By definition the point H is the unique point on AB produced such that CH is perpendicular to HB. If HB and AB did not lie in a straight line, HC would not be the altitude.
https://brilliant.org/wiki/triangles-circumcenter/
Because BA is horizontal, its position is central/symmetric; simply add another 10 to the right, for 10 + 8 + 10, which has to be equal to diameter 2r = 28, or r = 14.
Straight forward. Thank you!
Where is the proof that H-B-A is a straight line? Its something that your method definitely requires.
Log in to reply
Please read the problem statement closely. CH is defined as the altitude of triangle ABC (think “extended base”). Thanks.
The radius of the diagram is about 187 pixels wide on my screen. HA is about 241 pixels, or 18 units. This means the conversion of units to pixels is about *13.38. 187 divided by the conversion is very close to 14.
Although I did not do a detailed calculation as above I solved this in a similar way. I observed that the radius was equal to 10 (HB) plus half of AB. Half of eight (the length of AB) is 4, so r is in tota; 10 + 4 = 14.
Log in to reply
I didn't think of it that way at all. I was completely stumped but did see that the diagram is proportioned correctly and so I just measured it with a browser extension. Your solution is far better!
Log in to reply
Cheating. Lol
Log in to reply
@Pleayo Tovaranonte – Yeah I'm inclined to agree with that assessment, although there is something to be said for using all information at one's disposal when problem solving
Same technique! Yeah!!
I guesstimated also based on the pic being an accurate representation of those distances. But if OP drew the pic purposefully inaccurate, guessing wouldn't work. I am reading the comments to follow the mathematical solution...
easiest solution is.... the width of the horizontal chord is 8. the half length of the chord is 4. 10 + 4 is the half length of one side of the square the circle is inscribed in. hence... r = 1/2s. r`=14
But the picture doesn't seem to be on scale, the 8 units segments looks too munch shorter than the other
Please, this solution is a joke?
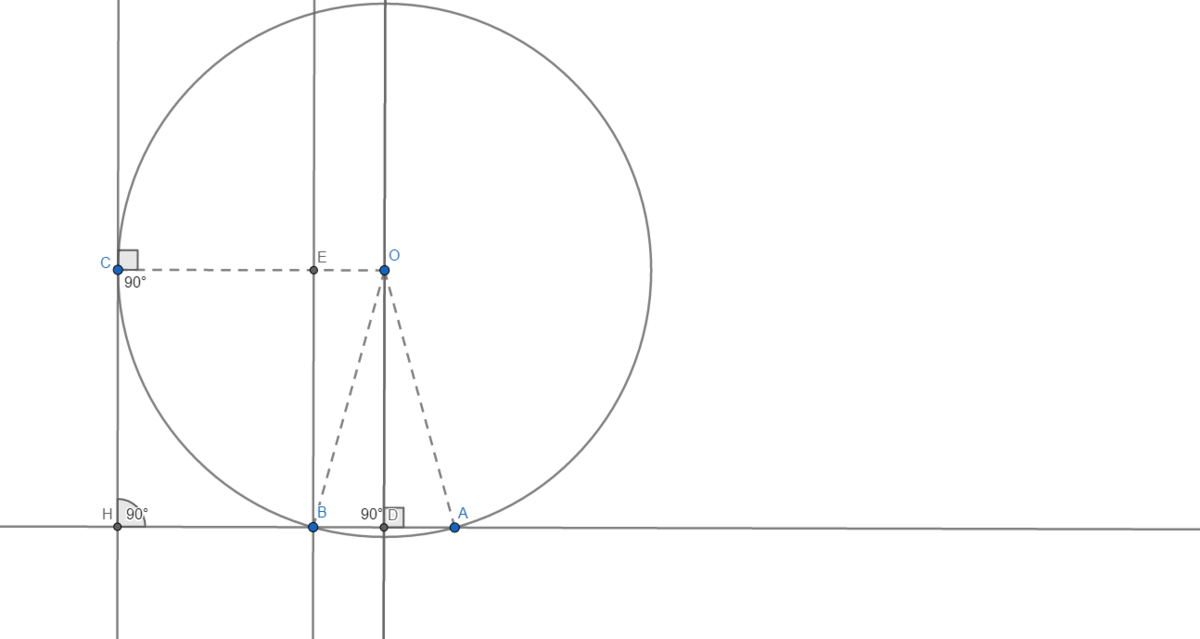
Construct radii OA and OB and OC, then OA = OB = OC because all radii in a circle are congruent. Since radii are congruent, it formed an isosceles triangle BOA that has congruent segments OA and OB. Then, construct an "altitude" OD. Since CH is an altitude and a radius and a tangent are perpendicular, angles CHA, ODH, and OCH measure 90 degrees. Since these three angles are right, angle COD is also right. Since these 4 angles are right, the quadrilateral CODH is a rectangle. From O to D, OD is a perpendicular bisector since triangle BOA is isosceles and then BD and AD is 4. Since BD = 4, construct segment BE that is parallel to OD, then EO = 4. In the diagram, if EO = 4, then CE = 10 because CEBH is a rectangle. CE + EO = CO = the measure of the radius. So, 10 + 4 = CO CO = 14
By Power of a Point Theorem,
C H 2 = ( H B ) ( B A )
⟹ C H = 1 8 0 = 6 5
By Pythagorean Theorem,
C B 2 = C H 2 + H B 2 , C A 2 = C H 2 + H A 2
⟹ C B = 2 8 0 = 2 7 0 , C A = 5 0 4 = 6 1 4
Also sin A = 6 1 4 6 5 = 1 4 5
Using the fact that 2 R = sin A C B , where R is the circumradius of the triangle
⟹ R = 1 4
From the circumference equation we know that: x 2 + y 2 = r 2
we also know from the problem that the following points are present in the circunference ( x 1 , y 1 ) = ( 1 8 − r , y ′ ) and ( x 2 , y 2 ) = ( 1 0 − r , y ′ ) . From that we can build a simple system to solve the problem:
{ ( 1 8 − r ) 2 + y ′ 2 = r 2 ( 1 0 − r ) 2 + y ′ 2 = r 2
Removing the term dependent on y ′ is easy and we just need to subtract one equation for the other. Solving the system will get us to ( 1 8 − r ) 2 = ( 1 0 − r ) 2 where taking the square root will give us a ( 1 8 − r ) = ± ( 1 0 − r ) where one can find that r = 1 4 .
☺
Why can you assume that y1=y2?
- CH=HB=10cm (tangents arising from the same point to a circle are equal )
- Circumradius-r
- formula for circumradius -** r=abc/4 area of triangle
- area of triangle =1/2 b h * =1/2 8*10=40
- Using pythagoras we can find the length of CB
- CH^2+HB^2=CB^2=10*(2^1/2)
- Similarly we can find AC
- AC=20.5
- Now putting all the values in the formula we get
- r=8 * 20 * 10/4*40 ( assuming 10(2^1/2) to be approximately 10 and 20.5 as 20)
- r=14
CH and HB are not equal!
Log in to reply
2 tangents arising from the same point to a circle are equal , it’s a property of tangents and circles
Log in to reply
The problem is that HB is not a tangent to the circle but slices through it, creating line AB.
Tricky but easy problem. No need to overthink and complicate things. By looking at the screen of your phone you can see the answer. 10+4= 14

Relevant wiki: Circles Problem Solving - Basic