Inscribed and Circumscribed Spheres.
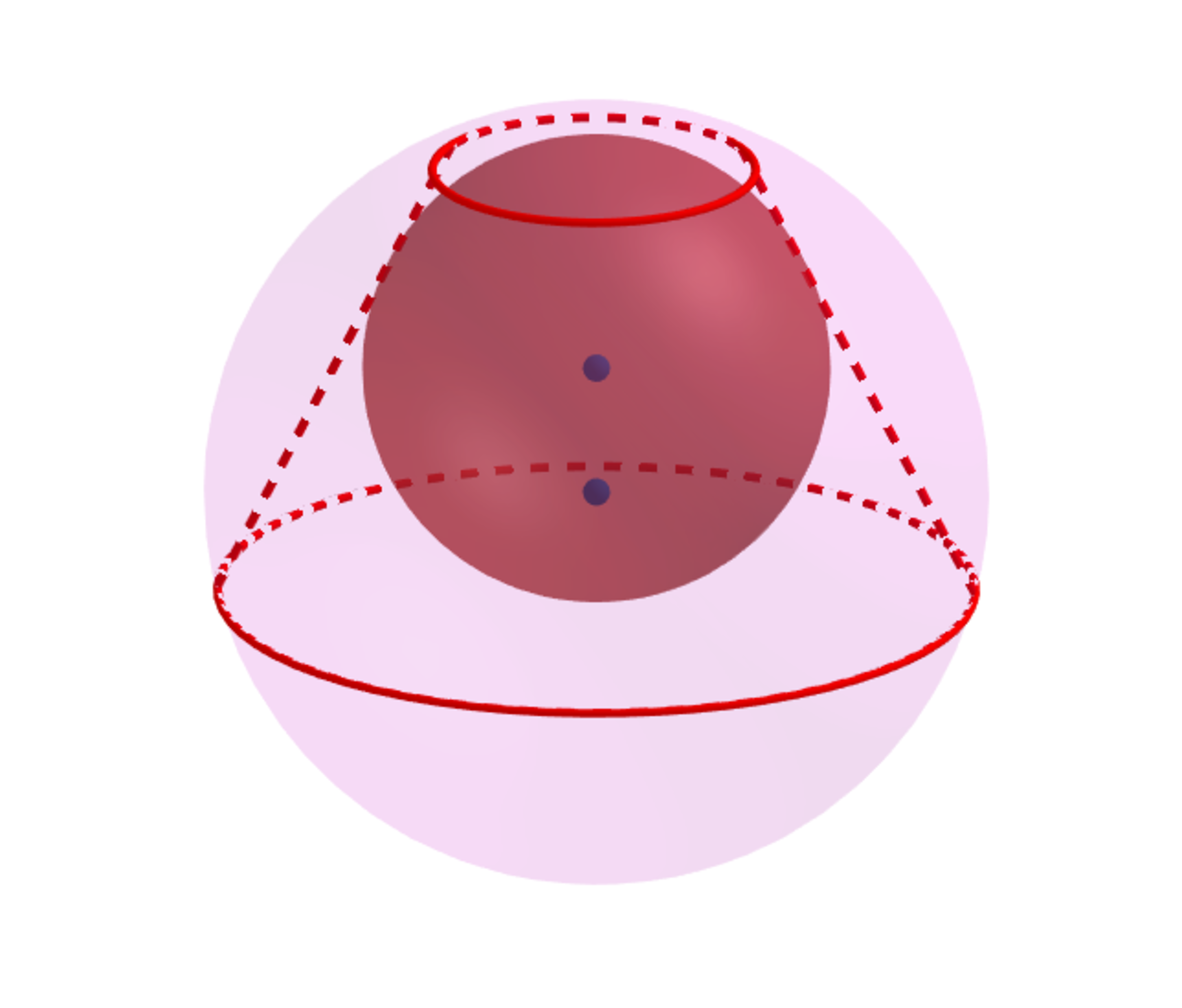
In the diagram above, a sphere is inscribed in a truncated cone such that the volume of the truncated cone is twice the volume of the inscribed sphere and another sphere is circumscribed about the truncated cone.
Let m be the radius of the smaller base of the truncated cone and R be the radius of the circumscribed sphere.
If m R can be expressed as m R = b a ( c + c ) , where a , b and c are coprime positive integers, find a ∗ b − c .
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Why not 0.375*(5+sqrt(5))?
Log in to reply
It can be simplified to 8 3 ( 5 + 5 ) .
Log in to reply
This is the same issue as the last problem, though - you only get that particular unsimplified form if you use a certain solution root. If you're simplifying along the way, you get the neater form posted by @Saya Suka .
Perhaps an alternative would be to ask for the value of the ratio; you can insist on a certain level of precision by asking for ⌊ 1 0 d ⋅ S ⌋ as a solution. I get that this hides the elegance of the "true" form, but it would avoid this issue.
(By the way, this is an elegant set of shapes - the golden ratio is cropping up everywhere in my solution.)
Log in to reply
@Chris Lewis – I would like to repost the problem using the simplified form, but people had done the problem already.
I restated the problem as follows:
If m R can be expressed as m R = b a ( c + c ) , where a , b and c are coprime positive integers, find a ∗ c + b .
This way the result is 1 9 .
By the way, you could write m R = 4 3 5 ϕ .
Log in to reply
@Rocco Dalto – I was about to say "good save" but isn't the ratio 8 3 ( 5 + 5 ) ? (So you could change the required answer to a b − c , I suppose!)
Log in to reply
@Chris Lewis – Thanks. I made a mistake and accidently wrote 4 3 .
First we find w in terms of m using the inscribed sphere below.
Using the fact that tangents to a circle from an outside point are congruent we obtain the diagram above.
The height h of the truncated cone is h = 2 r
Using right △ A B C we have:
( w + m ) 2 = ( w − m ) 2 + 4 r 2 ⟹ w 2 + 2 w m + m 2 = w 2 − 2 w m + m 2 + 4 r 2 ⟹ 4 w m = 4 r 2 ⟹ r 2 = w m ⟹
r = w m .
The volume of the inscribed sphere V s = 3 4 π ( w m ) 2 3
and
The volume of the truncated cone is V T = 3 2 π ( w 2 + w m + m 2 ) ( w m ) 2 1
V T = 2 V s ⟹ w 2 + w m + m 2 = 4 w m ⟹ w 2 − 3 w m + m 2 = 0 ⟹ w = ( 2 3 ± 5 ) m
Since m w > 1 we choose w = ( 2 3 + 5 ) m
Next we use the circumscribed sphere to find m R .
R 2 = z 2 + w 2 = R 2
R 2 = ( h − z ) 2 + m 2
⟹ z 2 + w 2 = h 2 − 2 h z + z 2 + m 2 ⟹ z = 2 h h 2 − w 2 + m 2
Using the values for w and h above and simplifying we obtain:
z = 4 2 3 + 5 7 + 5 m
Using R 2 = z 2 + w 2 and simplifying we obtain:
R = 4 3 3 + 5 5 ( 7 + 3 5 ) m ⟹
m R = 4 3 3 + 5 5 ( 7 + 3 5 ) = 8 3 5 ( 7 + 3 5 ) ( 3 − 5 ) =
8 3 3 0 + 1 0 5 = 8 3 ( 5 + 5 ) 2 = 8 3 ( 5 + 5 ) = b a ( c + c ) ⟹ a ∗ b − c = 1 9 .