Inscribed perimeter
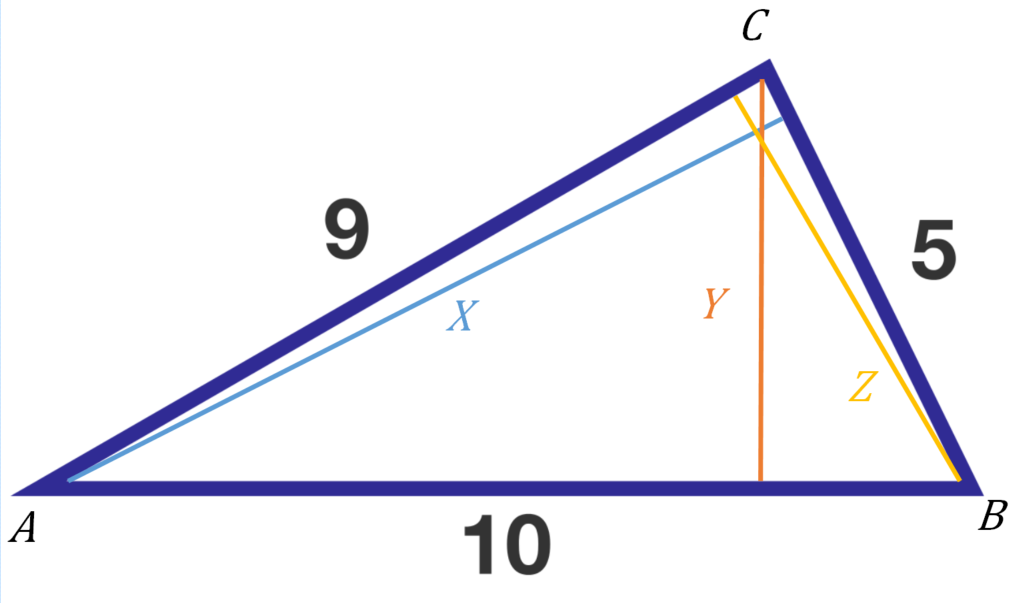
Suppose you inscribe a smaller triangle in the triangle below such that its three vertices are on different sides of the given triangle.
What is the smallest possible perimeter of the inscribed triangle?
The answer is 8.96.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
Where can I get the result of orthic triangle??
I wonder whether it is right to use the "Light always takes the shortest path" trick here, because I used and got it correct. Since incentre of orthic triangle is orthocentre of main triangle, this means orthic triangle is the path traced by a light ray if the three sides were mirrors.
Log in to reply
Forget it. It is clearly mentioned in the solutions below. Didnt see them before.
We can fix the vertices on the 9 and 10 sides as shown in the picture and then determine where to put the third vertex on the 5 side such that the sum of the two new sides is minimized. The sum of the two new sides is minimized when the angles with the 5 side are equal. This result is made obvious by reflecting one of the points across the 5 side (as shown in the second picture), and seeing that the shortest distance between any two points is a straight line.
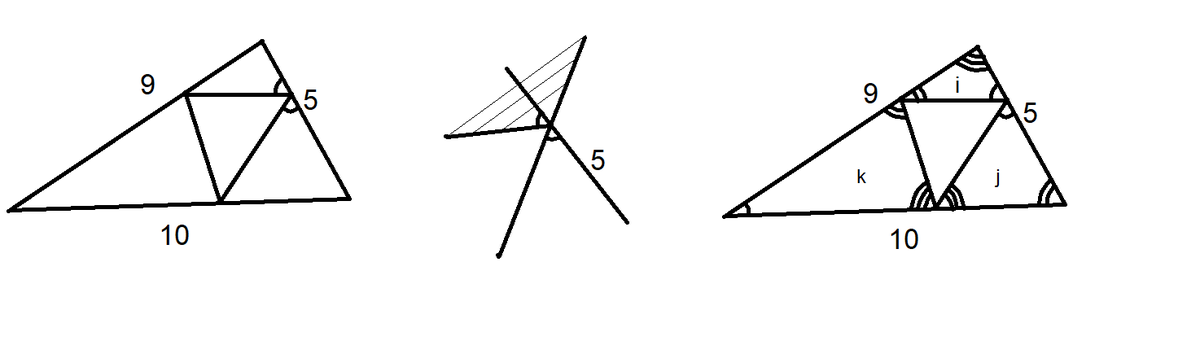
We can label the other two pairs of angles in the same way. Notice that the three straight angles have to add up to 540 degrees. Subtracting off the angles of the inscribed triangle and dividing by 2 tells us that the three angles we marked must add up to 180 degrees. With this fact we can label the angles of the of the original triangle. We have four similar triangles, so we can label the scaling factors of the three new triangles i , j , and k (scaled from the original triangle). By similar triangles, we can solve for the sides of the original triangle to get 5 i + 1 0 k = 9 , 9 k + 5 j = 1 0 , 1 0 j + 9 i = 5 . Solving this system gives i = 1 5 1 , j = 2 5 1 1 , k = 1 5 1 3 . The perimeter of the inscribed triangle is 1 0 i + 9 j + 5 k , so the answer is 8 . 9 6
That's the fastest way yet in coming up with 8 . 9 6 . But the orthic triangle is not the only one that has equal angles where its vertices meet the sides of the main triangle. How would you show that the orthic triangle in fact has the minimum perimeter?
Log in to reply
I am not quite sure what you are asking. I proved that the minimum total perimeter is acheived when corners of the inner triangle make equal angles with the side that they touch (as shown in the third picture). The third picture is the only way to make that happen, so I am not sure why you say that there can be multiple triangles that make equal angles. You can write and solve the system of equations directly from the picture and find the exact values. Is my logic incorrect? Do you have an example that has equal angles, but is not in the form of the picture?
Log in to reply
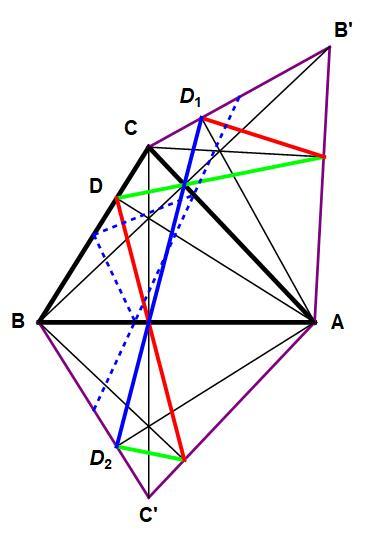
Okay, have a look at my figure with the refected triangles. Any blue line where C D 1 = C ′ D 2 is a path that makes equal angles with the sides. In fact, the litlte calculus exercise I included is for finding the one with the shortest path, which is the orthic triangle.
Log in to reply
@Michael Mendrin – I see the other two because of reflections, but what makes you say that the agle at point D is optic? If all three angles are optic, there is only one inscribed triangle of that form (and you can solve for it as shown by the system of equations.)
Log in to reply
@John Ross – I'm saying that points D 1 , D 2 can be chosen arbitrarily to create other optic "circuits".
Log in to reply
@Michael Mendrin – Yes, but for only one choice of C D 1 will the corner at D be optic, so there is only one completely optic circuit.
Log in to reply
@John Ross – Okay, I've revised my figure and solution, based on yours and Mark's comments.
I have added a note to my original comment. In your construction, and mine, we considered inscribed triangles with a fixed vertex D . We constructed a triangle D X Y which was "optical from D ", in the sense that equal angles were subtended at X and Y (and so a light beam emitted from D would return to D . The subtended angles at D did not have to be equal, The orthic triangle is the only inscribed triangle which is optical from all of its vertices. The construction here finds it, if it does not recognise the other properties of the orthic triangle.
Log in to reply
The added note says that given point D there can only be one optic circult starting and ending at D . However, as your original comment has pointed out, there are many "optical" triangles possible. Any optic path will make equal angles with the sides of the triangle. Using calculus, however tedious that is, does show that the orthic triangle has the least perimeter. What are other ways of showing it? You've described one way in your original comment.
Log in to reply
@Michael Mendrin – Given any D , the other two corners of the triangle will be "optical" (angle of incedence equals angle of reflection), but the corner at point D will not neccessarily be optical. Only for one particular choice of D will the corner at D be optical and there be a completely optical inscribed triangle. Given the 5-9-10 triangle, there is only one completely optical inscribed triangle.
@Michael Mendrin – For each point D , there is one “optical from D ” triangle, namely a triangle which would mark the first three legs of a light beam emitted from D that returns to D . In that sense, there are infinitely many “ optical from...” triangles. An “optical from D ” triangle has the smallest perimeter of all inscribed triangles possessing D as vertex. Choosing D to be the foot of the altitude from A , and picking the “optical from that D ” triangle then obtains the inscribed triangle with shortest perimeter, and no calculus. That was my argument in my original comment.
Of course, what happens is that the orthic triangle is the “optical from” triangle for each of its vertices , and not just for one vertex. This means that we have all the angles as in John’s proof...
Log in to reply
@Mark Hennings – Okay, this problem is getting to be more fun. Let me expand on that figure that I have.
Log in to reply
@Michael Mendrin – If D E F is the "optical from D " triangle where D is the foot of the altitude from A , and E , F lie on A C , A B respectively, then D E F is the inscribed triangle with smallest perimeter. It must therefore also be the "optical from E " and "optical from F " triangle, and hence (i) D E F is fully optical, (ii) E is the foot of the altitude from B , (iii) F is the foot of the optical from C . Thus D E F is indeed the orthic triangle
Log in to reply
@Mark Hennings – Okay, it seems like I've now come around the full circle. Let me revise the figure that I have and build on yours and Ross' comments.
This has given me a great idea for a new problem, let me think about that.
You have got i and k swapped in your equations (or else mislabelled in your diagram).
See Henning's explanation about the orthic triangle and his following comment below. In this figure, the blue line D 1 D 2 is the straight path through the refections of the triangle, so that it makes equal angles with the sides of the triangle at the feet of the altitudes of the triangles, as if a ray of light bounced the sides of the triangle to the point of beginning. Necessarily, C D 1 = C ′ D 2 . The blue line D 1 D 2 is shortest when A D 1 = A D 2 is shortest, or the base of the altitude of triange A B C . The dotted blue line (which does not have minimum perimeter) also makes equal angles with the triangle except where it touches side B C . Only the orthic triangle makes equal angles with the triangle at all three vertices. Please see John Ross' elegant solution to this, based on the similarity of smaller triangles with triangle A B C .
The dimensions of the triangle has been altered for clarity.
One can instead make this a calculus problem by finding the mininum length of the blue line, given the condition that it must start and end in the same place, from D 1 to D 2 , involving a single variable proportional to C D 1 . Let's try that.
Given triangle with sides ( 9 , 5 , 1 0 ) as shown above in the problem statement, with the left bottom vertex at ( 0 , 0 ) . Let k = C B ′ C D 1 = C ′ B C ′ D 2 . Then the coordinates of the top and the bottom ends of the blue line are
(
1
2
5
3
(
3
2
5
+
3
4
7
k
)
,
1
2
5
6
1
4
(
2
5
+
1
9
k
)
)
(
5
3
9
(
1
−
k
)
,
−
5
6
1
4
(
1
−
k
)
)
so that the mininum distance is 8 . 9 6 at k = 2 7 1 , and the blue line passes through the feet of altitudes as shown.
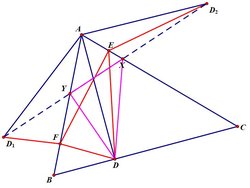 Your geometric argument is not quite complete, since there are many "optical" triangles that can be inscribed in an acute-angled triangle. Fix a point
D
on the line
B
C
and consider an inscribed triangle
D
E
F
with
D
as vertex. Reflect
D
in both
A
B
and
A
C
to form
D
1
and
D
2
respectively. Then
D
1
F
+
F
E
+
E
D
2
is equal to the perimeter of
D
E
F
, and hence the perimeter of
D
E
F
is greater than or equal to
D
1
D
2
, and we can find an inscribed triangle with perimeter
D
1
D
2
with
D
as vertex by picking the "optical" triangle
D
X
Y
. We have an optical triangle for each point
D
, and so need to choose the point
D
to give the optical triangle with smallest perimeter.
Your geometric argument is not quite complete, since there are many "optical" triangles that can be inscribed in an acute-angled triangle. Fix a point
D
on the line
B
C
and consider an inscribed triangle
D
E
F
with
D
as vertex. Reflect
D
in both
A
B
and
A
C
to form
D
1
and
D
2
respectively. Then
D
1
F
+
F
E
+
E
D
2
is equal to the perimeter of
D
E
F
, and hence the perimeter of
D
E
F
is greater than or equal to
D
1
D
2
, and we can find an inscribed triangle with perimeter
D
1
D
2
with
D
as vertex by picking the "optical" triangle
D
X
Y
. We have an optical triangle for each point
D
, and so need to choose the point
D
to give the optical triangle with smallest perimeter.
Now A D 1 D 2 is isosceles, and ∠ D 1 A D 2 = 2 ∠ A , and hence D 1 D 2 = 2 A D sin ∠ A . Thus the perimeter of the optical triangle with vertex D is made as small as possible by choosing D so that A D is as small as possible. Thus D must be the foot of the altitude from A , and we do obtain the orthic triangle as the inscribed triangle with least perimeter.
NB The triangle D X Y and its brothers are "optical" at D , in the sense that a light beam emitted from D and reflected off the other two sides of the original triangle will return to D . A light beam emitted at X will not return to X , since the subtended angles at D are not, in general, equal. The orthic triangle is the only triangle which is optical with respect to each of its vertices.
Log in to reply
I'll refer to your comments to complete the explanation, noting that the distances between the vertices (such as AD) be made as small as possible.
One could make this an optimisation problem indeed
Please what got this to do in our daily life ... i like maths but i dont meet such equations on field or in anywhere... but we always learning it.
This solution is by no means elegant or even that mathematical, but if this problem was to be solved in under 30 seconds here is how to do it. First, let's consider some easy triangle like an isosceles triangle and let's imagine we had to find the smallest possible perimeter of the inscribed triangle. Intuitively, it would look something like this:
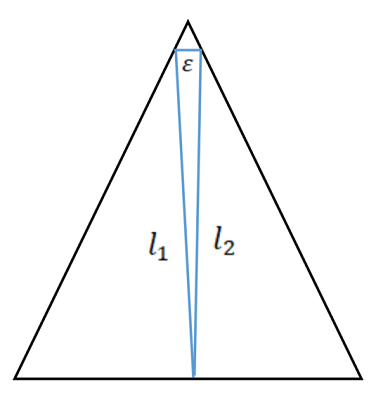 Where
ε
is some tiny distance, so we can say
l
1
=
l
2
. Since we are minimizing distance
l
1
and
l
2
are perpendicular to the line on the base of the triangle. Now finding the smallest perimeter is merely calculating 2
×
l
1
or 2
×
l
2
(not that it matters).
Now let's consider the triangle given:
Where
ε
is some tiny distance, so we can say
l
1
=
l
2
. Since we are minimizing distance
l
1
and
l
2
are perpendicular to the line on the base of the triangle. Now finding the smallest perimeter is merely calculating 2
×
l
1
or 2
×
l
2
(not that it matters).
Now let's consider the triangle given:
 The line
Y
seems to be the shortest (one could check, but we will proceed assuming
Y
is the shortest).
Since
Y
⊥
A
B
we can form a right triangle at
∠
A
B
C
where the side
Y
multiplied by
2
will give the smallest perimeter. First to find
∠
A
B
C
we use the cosine law.
The line
Y
seems to be the shortest (one could check, but we will proceed assuming
Y
is the shortest).
Since
Y
⊥
A
B
we can form a right triangle at
∠
A
B
C
where the side
Y
multiplied by
2
will give the smallest perimeter. First to find
∠
A
B
C
we use the cosine law.
∠ A B C = cos − 1 ( − 2 ( A B ) ( B C ) A C 2 − A B 2 − B C 2 ) = cos − 1 ( − 2 ( 1 0 ) 5 ) 9 2 − 1 0 2 − 5 2 ) = 6 3 . 8 9 6 ∘
From here, we use sin ratio (since Y ⊥ A B ) to calculate the distance from A B to the vertex C which is Y
Y = 5 × sin 6 3 . 8 9 6 ∘ = 4 . 4 8 9 9
So the smallest perimeter is P = 2 ( Y ) = 2 ( 4 . 4 8 9 9 ) = 8 . 9 7 (yes this is slightly off, but much easier)
I applaud your attempt to solve this in under 30 seconds. This only works in this case because the triangle is close to right angled and two of the feet of the altitudes you've drawn (which is actually the real clue) are close together.
Strangely, you've drawn an acute isosceles triangle to develop an intuition. It is much clearer in an obtuse isosceles triangle.
It is very interesting to think about this problem in a way of physics. Suppose the three sides of the given triangle are three rigid rods with zero friction. Then we put a elastic band around the rods, and it will surely try to shrink to a minimum length. And by analyzing the forces in the final balance, the conclusion of orthic triangle will be obvious.
That is an interesting approach, but how it is immediately obvious that the forces cancel out only in the case of the orthic triangle?
Log in to reply
The angles between one side of the original triangle and two sides of orthic triangle are the same.
What a cool solution. Here I was trying to minimize the sum of distances in function of the given angles, when it could have been so obvious.
Calculated the (x,y) cordinates of the given triangle and it's orthic triangle and the perimeter= (13/3)+(2/3) +(99/25) = 8.96,
Answer=8.96
I solved the problem by using analytic geometry concepts, setting intersection of lines 9, and 10 as (0,0) and setting intersection of lines 5 and 10 as (10,0). Then, I solved for the point of intersection of lines 9 and 5 using the concepts of distance formula. I solved it to be (7.8, 4.4899).
I generalized a certain triangle with vertices as lying in the 3 lines. Thus, I expressed perimeter as an equation dependent on 3 variables.In this equation, it is composed of 3 addends: length of arbitrary point from 9 to 10, length of arbitrary point from 10 to 5, length of arbitrary point from 5 to 9.
Then, I created a Python code and used exhaustive enumeration with 0.01 increments in substituting it in the equation. I generated the minimum perimeter as 8.979977728257978.
I solved this for 2 hours, (1 and a half hour for the written solution, 30 minutes for the Python code). Wew. Got it correct, I guess.
Seemed like if it had been an quilateral triangle, the answer would have been “half the perimeter of the original” but 12 was wrong, so I figured it was a related number. I guessed 9 and the app rounded down. I don’t really think this was a clever solution, so why I’m really here just asking why it worked well enough?
To minimize the perimeter of this triangle, it is best to use points around the incenter of the triangle. This means that the triangle we seek is formed by the triangle's 3 points of tangency with it's incircle. Using a bit (a lot) of cheating from https://www.triangle-calculator.com/?what=sss&a=9&b=5&c=10&submit=Solve , I got this graph:
https://www.desmos.com/calculator/in5bn70a9y
Then, by finishing with the Pythagorean Theorem and adding up all the lengths of the triangle we get 8 . 9 6 .
I guessed and got it right on my second try
Although the more precise answer appears to be 8.96, my answer of 8.981 was also accepted as correct.
To arrive at this answer, I first determined that the smallest internal triangle will be an infinitely acute triangle with its 2 longest sides running from the longest side of the outer triangle (the side of length 10) to two points infinitely close to the outer triangle's opposite vertex (the vertex connecting sides of length 9 and 5).
I calculated the height of the triangle (the distance between that vertex and the side of length 10) to be 4.49. I then accepted 4.49 as the length of the 2 longest sides of the inter triangle.
With just 3 significant digits to work with, I estimated that the length of the inner triangle's 3rd side (connecting the outer triangle's sides of length 9 and 5) to be .001.
Addition to find the perimeter of the inner triangle: 4.49 + 4.49 + .001 = 8.981.
My conclusion: Given the precision in the other solutions, I'm surprised that 8.981 is an acceptable answer. And at the same time, despite the precision of the other solutions, I also don't understand how the perimeter of the inner triangle can be smaller than 8.98 (or twice the height of the outer triangle, or 2 * 4.49).
Let theta = the angle included between the sides of length 9 and 5. By the Law of Cosines, cos theta = 1/15 and sin theta = (4/15)sqrt 14. Let C be the vertex of theta and let F be the foot of the altitude from C. By Heron's formula the area of the triangle is 6sqrt 14, CF = (6/5)sqrt 14. Let X and Y be images of F upon reflection in the sides of length 9 and 5 respectively. Since CX = CF = CY, triangle XCY is isosceles with base XY equal to the perimeter, P, of the inscribed triangle of minimum perimeter (orthic triangle))...Why? Now notice that angle XCY = 2theta, so dividing triangle XCY into two congruent right triangles yields the equation (XY/2) / CX = (XY/2) / CF = XY/(2CF) = sin theta, or equivalently, XY/ ((12/5)sqrt 14) = (4/15)sqrt 14. Therefore, the perimeter P of the inscribed triangle of minimal perimeter = XY = 224/25 = 8.96.

It is a standard result that the inscribed triangle in an acute-angled triangle with the shortest perimeter is the orthic triangle, which has the feet of the altitudes as vertices.
This triangle is acute-angled (just), and the orthic triangle has side lengths a cos A , b cos B , c cos C . Thus the minimum perimeter is P = a 2 b c b 2 + c 2 − a 2 + b 2 a c a 2 + c 2 − b 2 + c 2 a b a 2 + b 2 − c 2 = 2 a b c 2 ( a 2 b 2 + a 2 c 2 + b 2 c 2 ) − ( a 4 + b 4 + c 4 ) which makes the minimum perimeter 8 . 9 6 for this triangle.