Inscribing Circles
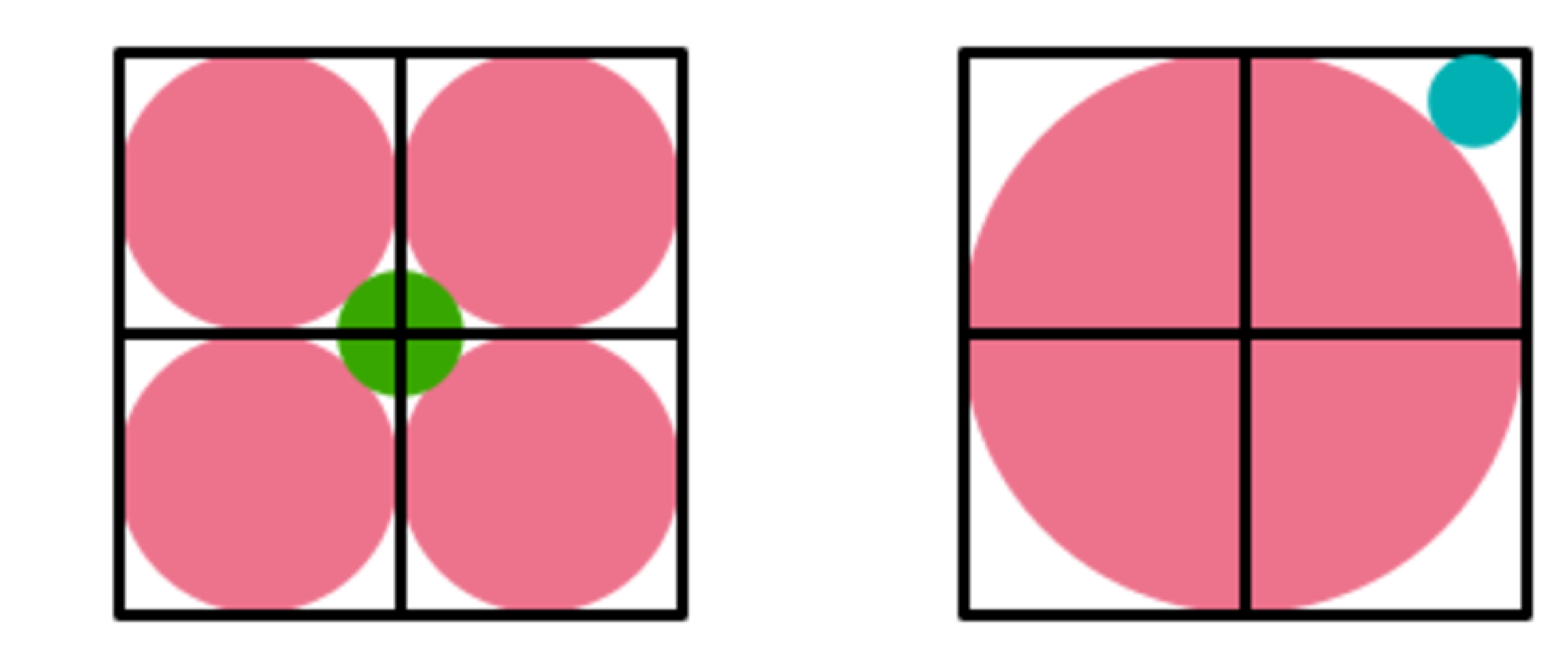
Which circle has a larger area, the green circle or the blue circle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
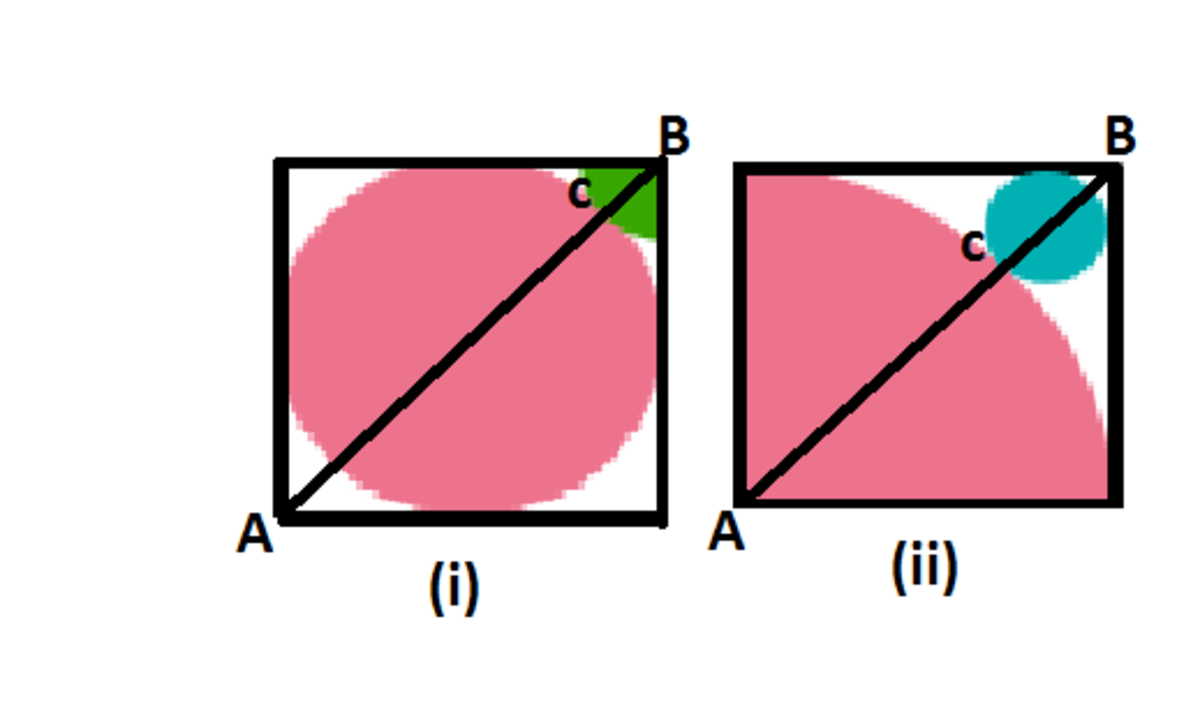
There is a quick way of knowing the fact by visualizing the picture. Keeping another identical green quarter at bottom left corner of figure (i) completely completes the diagonal length while small area is left out in figure (ii) which implies that area of green circle must be greater
Here is the lengthier way, where we figure out the lengths.
Here is the a quarter of each square.
Let the length of each quarter be x .
In fig (i),
AB = x 2
Diameter (pink) = x
Also,
Since there is space for another green circle quarter in the bottom left
Diameter (pink) + 2 Radius (green) = AB
x + 2 Radius (green) = x 2
Radius (green) = 2 x 2 − x -----------------------------------(i)
In fig (ii)
AB = x 2
Radius (pink) = x
Since the circle doesn't touch the vertex of square
Radius (pink) + Diameter (blue) < AB
x + 2 Radius (blue) < x 2
Radius (blue) < 2 x 2 − x --------------------------------------(ii)
From (i) and (ii),
Since, Radius (blue) < Radius (green)
So, Area of green circle > Area of blue circle
Yes, that's the idea that I had. Do you see a pictorial way to state the inequality so that it falls out immediately?
Log in to reply
Yes, keeping another green quarter at bottom left corner of figure (i) completely completes the diagonal length while small area is left out in figure (ii)
Log in to reply
Perfect! Could you add that version? It makes reading the rest of your solution much clearer.
Log in to reply
@Calvin Lin – Thank You Sir. I have made the changes
This graphic should be self-explanatory, as to why the blue circle has less area than the green circle. Note that the big blue circle has the same area as four of the small blue circles which have half the diameter.