Inscribing Regular Polygons in Circles

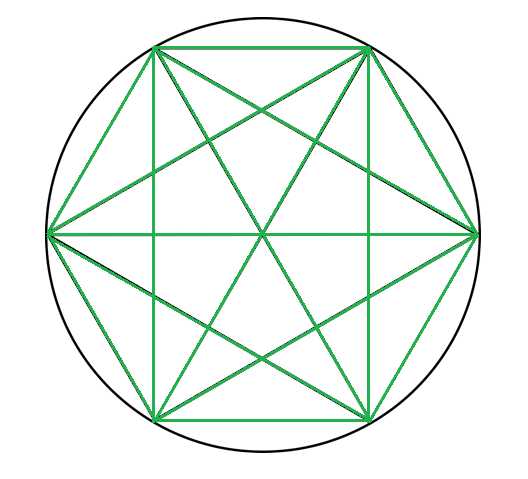Let $O$ be the centre of the circle. If we draw a line segment from $O$ to every vertex, this would divide the circle into $n$ equal parts. Therefore, for each pair of vertices $A,B$ there must be a integer $k$ with $1 \le k \le \dfrac{n}{2}$ such that $\angle AOB = \dfrac{2\pi k}{n}$ .

Suppose first that $n$ is odd. Then for each $1 \le k \le \dfrac{n-1}{2}$ , there are exactly $n$ line segments $AB$ such that $\angle AOB = \dfrac{2\pi k}{n}$ . (Why that? Because there is exactly one line segment that starts from each vertex and goes counterclockwise by the specified angle.)

Now it's fairly simple to prove that if $\angle AOB = \dfrac{2\pi k}{n}$ , then $AB = 2\sin{\left(\dfrac{\pi k}{n}\right)}$ . Since there are exactly $n$ line segments of each length, we get the formula: $L_n = \sum_{k=1}^{\frac{n-1}{2}} 2n\sin{\left(\dfrac{\pi k}{n}\right)}$ $\frac{L_n}{n^2} = \frac{2}{n}\sum_{k=1}^{\frac{n-1}{2}} \sin{\left(\dfrac{\pi k}{n}\right)}$ Now let's rewrite this as a Riemann sum. Let $f(x) = \sin{\pi x}$ , and $x_k = \frac{k}{n-1}, x^{*}_k = \frac{k}{n}$ for $0\le k\le \dfrac{n-1}{2}$ . Then $\dfrac{k-1}{n-1} < \dfrac{k}{n} <\dfrac{k}{n-1}$ so $x_{k-1} < x^{*}_k < x_{k}$ . Furthermore, we have $x_k - x_{k-1} = \dfrac{1}{n-1}$ .

Therefore, our expression can be rewritten as follows: $\dfrac{L_n}{n^2} = \dfrac{2(n-1)}{n} \sum_{k=1}^{\frac{n-1}{2}} f(x^{*}_k)(x_k - x_{k-1})$ Therefore we do indeed have a Riemann sum. Now $x_0 = 0$ and $x_{(n-1)/2} = \frac{1}{2}$ , so as $n$ approaches infinity, we get: $\lim_{n\to\infty} \frac{L_n}{n^2} = \lim_{n\to\infty}\frac{2(n-1)}{n} \int_{0}^{1/2} \sin{(\pi x)} dx = 2 * \frac{1}{\pi} = \boxed{\dfrac{2}{\pi}}$ Note that if $n$ is even, we get a similar formula: $\frac{L_n}{n^2} = \frac{1}{n}\left(-1 + \sum_{k=1}^{n/2} 2\sin{\frac{\pi k}{n}}\right)$

This solution is kinda sketchy just saying.

As n approaches infinity, we are looking at a circle inscribed in a circle (it's circleception :3 lol)

Fix a point $T$ on the circle's circumference. Draw a radius from the circle's center $O$ and place another point $S$ on the circle's circumference. Label angle $\angle SOT=\theta$ and line segment $\overline{ST}=x$ . We are looking at the average length of $x$

By law of cosines $x^2=2+2\cos(\theta$ )

$x^{2} = r^{2}+r^2- 2 r^2\cos(\theta)) = 2r^{2}(1 - (2\cos^{2}(\frac{\theta}{2}) - 1)) =$

$4r^{2}(1 - \cos^{2}(\frac{\theta}{2})) = 4r^{2}\sin^{2}(\frac{\theta}{2})$

$\Longrightarrow x = 2r\sin(\frac{\theta}{2})~\text{for} 0 \le \theta \le \pi.$

Using probability distribution function

$\displaystyle\dfrac{1}{\pi}\int_{0}^{\pi} 2r\sin(\frac{\theta}{2}) d\theta = \dfrac{4r}{\pi}\int_{0}^{\pi} \sin(\frac{u}{2}) du = \dfrac{4r}{\pi}[-\cos(\frac{\pi}{2}) - (-\cos(0))] = \dfrac{4r}{\pi}$

Here $r=1$ so we have the average length equal to $\dfrac{4}{\pi}$

The number of diagonals in a figure is $\dfrac{n(n-3)}{2}$ . To include the number of sides this becomes $\dfrac{n(n-1)}{2}$ .

Multiplying the number of diagonals by the average diagonal length (remember that this only works as n approaches infinity).

$L_n=\left(\dfrac{4}{\pi}\right)\cdot\left(\dfrac{n(n-1)}{2}\right)= \dfrac{2n (n-1)}{\pi}$

Dividing through by the number of sides gives us $\dfrac{2 (n-1)}{n\pi}$

As $\displaystyle \lim_{n\rightarrow \infty} n=\displaystyle \lim_{n\rightarrow \infty} (n-1)$

Thus our result is

$\displaystyle \lim_{n\rightarrow \infty}\dfrac{L_n}{n^2}=\displaystyle \lim_{n\rightarrow \infty}\dfrac{2 (n-1)}{n\pi}=\dfrac{2}{\pi}\approx \boxed{0.637}$