Inspired by Abhay Kumar
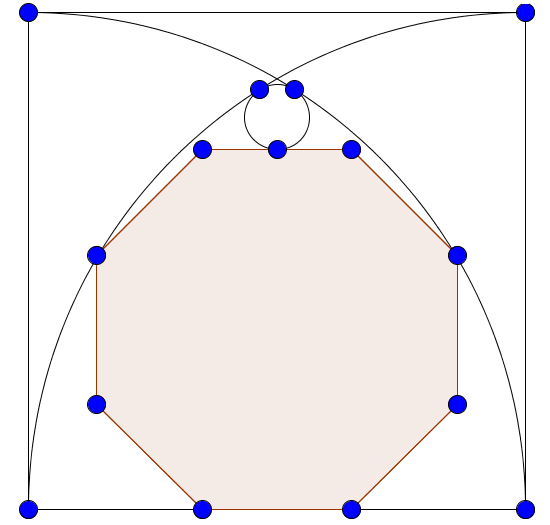 Two quarter circles are inscribed in a square of side length 5. A regular octagon is inscribed in between the two quarter circles and a circle of radius
is inscribed in between the regular octagon and the two quarter circles. What is
?
Two quarter circles are inscribed in a square of side length 5. A regular octagon is inscribed in between the two quarter circles and a circle of radius
is inscribed in between the regular octagon and the two quarter circles. What is
?
The answer is 0.33489.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
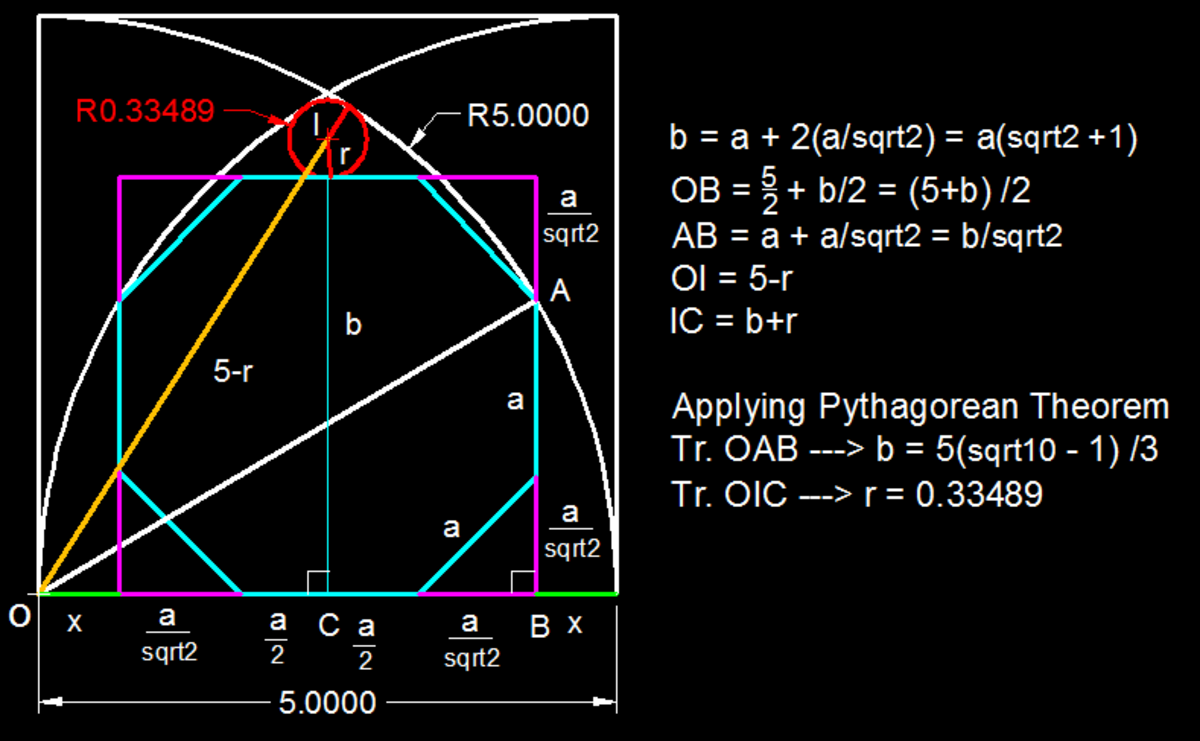
Let a be the side of the 8-gon. To simplify calculations, I have introduce a variable X = a ∗ ( 2 + 1 )
Solving right triangle GBE will give us the value of X. How to obtain the side lengths is shown in middle top Fig.
The top last Fig. shows GBE with sides in term of X.
On applying Pythagoras Theorem we get a quadratic,
4 3 ∗ X 2 + 2 5 ∗ X − 4 1 ∗ 7 5 .
On solving to get a +tive answer we get X = 3 5 ∗ ( 1 0 − 1 )
After getting the value of X, solving right triangle ODE will give us the value of r. How to obtain the side lengths is shown in bottom two Fig.
The last bottom Fig. gives the right triangle ODE in terms of X, r and constants.
Solving this by Pythagoras Theorem we directly get value of r, since we now know the value of r. the r 2 term is canceled off.