Inspired By Arjen Vreugdenhil

First let us see if there actually exist $x,y\in \mathbb{R}$ satisfying the above equations. Hence we use the identity:

$x^2+y^2=(x+y)^2-2xy=3^2-2(5)=9-10=-1$

But since $x,y\in \mathbb{R}$ , we have $x^2+y^2\geq 0$ and above we are getting $x^2+y^2=-1$ which is less than $0$ . Hence , a contradiction and no solution exists for the given system.

$AM=\frac{3}{2}$ and $GM=\sqrt{5}>2$ , violating $GM\leq AM$ for positive real numbers. There is no solution.

$\textbf{Method 1}$ We know, For real numbers $x,y$ . $\large \begin{aligned} (x-y)^2\geq 0\\& \implies (x+y)^2-4xy\geq 0 \\&\implies xy\leq \dfrac{(x+y)^2}{4}=\dfrac 94=2.25\end{aligned}$ But here $xy=5>2.25$ - A contradiction. Hence $\textbf{No Solutions exist}$ . $\textbf{Method 2}$ Placing value of $x$ from $xy=5$ . $x+\dfrac{5}{x}=3$ $\implies x^2-3x+5=0$ Discriminant of this equation is negative hence no real $x$ and as a result no real $y$ exist. $\textbf{Method 3}$ Clearly graphs of $x+y=3$ and $xy=5$ does not give any common $x,y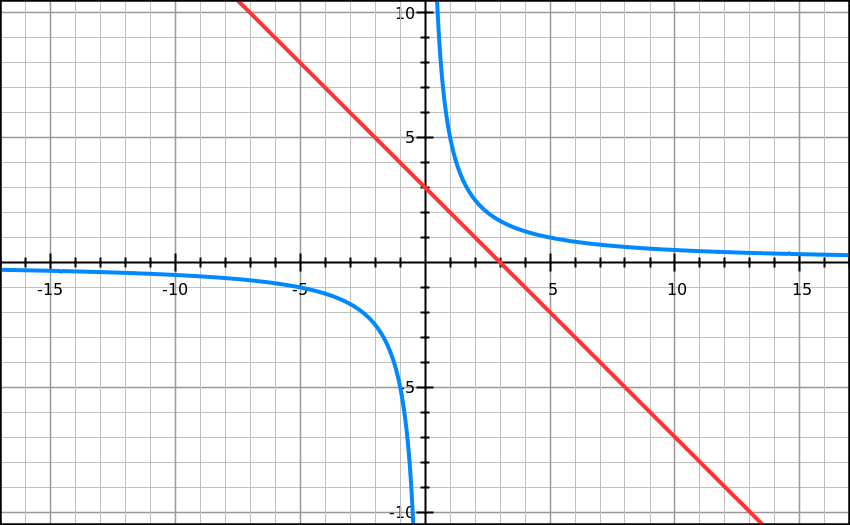$ . In fact, $x+y=2\sqrt 5$ is the line which is parrallel to the given line and is tangent to the curve $xy=5$ while the line in the question is at less distance than this line from origin hence no common point.

X = 3 -Y
X x Y =(3-Y)Y = 5
Y^2 -3Y + 5
b^2 - 4ac =-11
The roots of this equation are imaginary. So there are no real solutions.

With a problem carrying my name, least I can do is submit an alternative solution :)

Lemma : Under the constraint $x + y = c$ the maximum value of $xy$ for real $x, y$ occurs when $x = y = c/2$ .

Application: In this case, that maximum value is $xy = (3/2)^2 = 2\tfrac14$ . Therefore there are no real solutions for $xy = 5$ .

Proof of the lemma : quadratic functions have a vertex; here that is clearly a maximum, because we can make $xy$ very strongly negative by letting $x =$ very big number and $y = 3-x$ ; finally, symmetry requires that the maximum is reached when $x = y$ . Of course there are more boring, symbolic proofs, but this is more fun.

$\begin{aligned} &(x + y)^3 = x^3 + y^3 + 3xy(x + y) \\ &\therefore x^3 + y^3 = (x + y)^3 - 3xy(x + y) \\ &\therefore x^3 + y^3 = -18 \end{aligned}$

But wait, let's observe the conditions given we have:-

$\begin{cases} x+y&=&3 \\ x\times y&=&5 \\ x^3 + y^3 &= &-18\end{cases}$

Now observing the $3^{rd}$ case we can say that $x$ and $y$ cannot be positive real number as $x^3 + y^3 = -18$ . Assuming $x$ is negative and $y$ is positive such that $|x| > |y|$ , may satisfy the $3^{rd}$ condition but it will not satisfy $2^{nd}$ condition which says that $xy = 5$ since we have assumed $x$ is negative, product cannot be positive. Same goes if we assume $y$ negative and $x$ positive.

Another way that may satisfy the condition is that both $x$ and $y$ are negative. It may satisfy $3^{rd}$ and $2^{nd}$ condition but not $1^{st}$ condition that is $x + y = 3$ . Sum cannot be positive if both $x$ and $y$ are negative!!

Observing all the possible conditions, we can say that no real values can satisfy above conditions.

Squaring equation 1 we get $x^2+y^2+2xy=9$ . From equation 2 se get that $x^2+y^2=-1$ . This is not possible as square of any real number is always non-negative. Hence no real solution.

$(x-y)^2 \ge 0$

or, $(x+y)^2 \ge 4xy$

Here, $3^2 < 4.5$ . Thus no solution exists

From the system, we see that $x$ and $y$ are the roots of the equation $X^2-3X+5=0$ which has no roots so the correct answer is "No solution exist"