Inspired by Chester Robinson
What is the minimum number of straight lines that are needed to cover all 16 spots if you were using a pen that could not be removed from the page?
Treat the spots as a 0-dimensional object. They do not have length or width.
Treat the lines as a 1-dimensional object. They do not have width.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
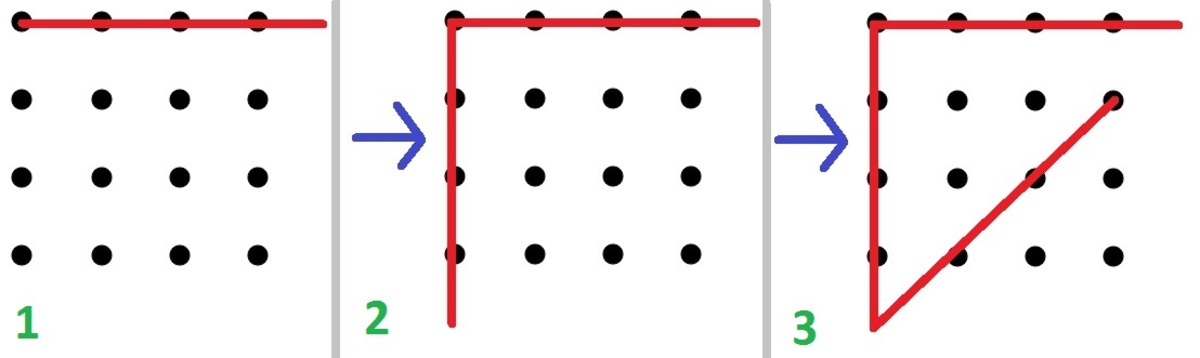
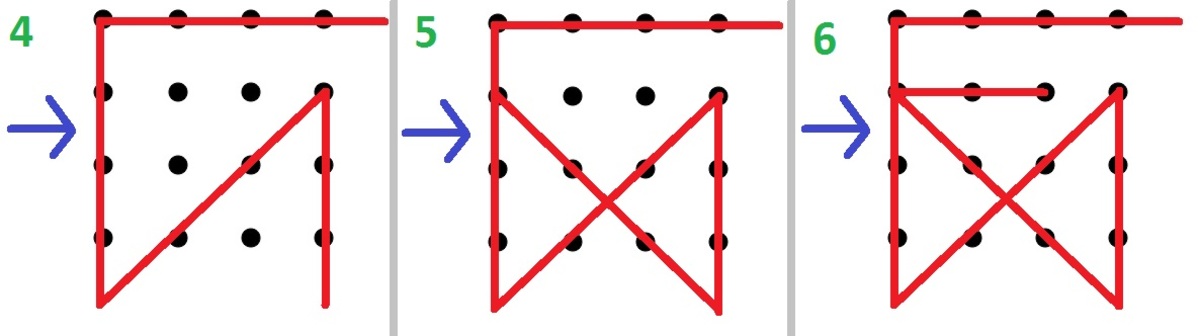
Nice visual explanation! In fact, we can see the 3 by 3 case in the lower right corner :) This is how the induction approach starts off.
Note that you would also need to show that it cannot be done with 5 lines.
Log in to reply
Thanks! I'll figure out a way to prove that it cannot be done with 5 lines. It'll be a fun challenge haha.
Read this note which generalizes the problem .
There are 2 parts to this construction question:
1. First, show that this can be done with 6 lines. We suspect that this is the answer.
2. Next, show that this cannot be done with 5 lines. This shows that 6 is indeed the minimum.
Label the columns from A to D (from left to right) and label the rows from 1 to 4 (from top to bottom). Now start from C3 and go to D2 and beyond, before going to the left to A1. From there diagonally make a L shape until you go slightly beyond D4. Then go diagonally to B2, before finally going down to B3.
Now we need to prove that the task can't be done in 5 or less goes. If you've got 4 goes then you need to get 4 dots per go. However, if you draw any line you will immediately get options of which none offer 4 collinear dots, as one is taken from your starting position.
To attempt to complete the task in 5 lines, means drawing one line of 4, because if we have a line of 3: 4 1 3 = 3 r 1 > 3. Now this leaves us with the challenge of trying to cover 12 dots in 4 moves, so 3 dots have to be covered each time. If we start from a main diagonal then there are only choices for paths (which are symmetrical). After choosing one we are left with 3 possible triples, but they all have one point in common so 3 lines isn't enough! The only other option is to avoid the main diagonal altogether and draw an U-shape where we are left with no more triples. Hence, our proof is complete :)
Note that it is not necessary that the dots are evenly distributed across all the lines. We could possibly have 2 vertical lines with 4 dots each, and then 3 other lines with 2-3 dots on them.
The natural follow on question: Can you generalize?
Log in to reply
Given the pattern for an n by n grid, n ≥ 3 , with the fewest lines, we can always embed this pattern in the minimal pattern for an ( n + 1 ) by ( n + 1 ) grid and add two lines covering the "new" dots, (connecting them at one of the ends to the embedded pattern), to complete the new pattern. So given that the minimal number of lines for a 3 by 3 grid is 4 , (call it P 3 = 4 ), we will have P n = 4 + ( n − 3 ) ∗ 2 = 2 ( n − 1 ) . Perhaps this only serves as an upper bound, but I can't see how we can go from n to n + 1 , n ≥ 3 , and have P n + 1 = P n + 1 .
(For n = 2 it would appear that P 2 = 3 , so the formula doesn't apply for this value. I guess that P 1 = 1 if a line can be a dot, :) )
Log in to reply
RIght. There is a very simple way to extend from P n to P n + 1 by adding 2 more lines in a spiral nature.
The harder part would be to show that P n = 2 n − 2 (for n ≥ 3 ) is indeed the minimum.
To do this, think about the number of horizontal lines, vertical lines and diagonal lines.
Log in to reply
@Calvin Lin – Was your approach similar to the one I outlined in your generalization note, or is there a simpler way of looking at the problem?
To point out, a common mistake made in arguing that 2 n − 2 is indeed the lower bound, is to assume that P n + 1 must be built from a configuration of P n . Especially in this problem, there is no reason why we can assume that there exists a P n in the best P n + 1 configuration.
In these type of construction cases, forward induction rarely applies. Backward induction might be applicable, but only if we can guarantee that the is a P n in every P n + 1 , which could be hard to show.
but wouldn't those 2 vertical lines have to connected such that you would have 3 lines connecting 8 dots
Log in to reply
Right, but that is not stated, nor clearly argued, in your proof.
Log in to reply
@Calvin Lin – Plz mention whether diagonals were allowed....moron....if diagonal lines weren't then how many minimum lines it would take???
N another one for you... A train 100 metres long travelling at 40 knots per hour passes an oncoming train travelling at the same speed...all you need to do is tell me how old is my father.... Hint: I'm crazy....not completely....pessimistic approach half empty glass sorts
For n x n the number of minimum lines = [n + (n - 2)] = 2(n - 1).
Log in to reply
While I agree it can be done with 2 n − 2 lines, it's not immediately clear to me that's the minimum. Do you know how we can establish that?