Just Find Its Antiderivative Right?
Evaluate the Riemann integral
∫ 0 1 x 1 d x .
Note : The Riemann integral of f equals S if the following condition holds:
∀ ϵ > 0 , ∃ δ such that for any tagged partition x 0 , … , x n and t 0 , … , t n − 1 whose mesh is less than δ , we have
∣ ∣ ∣ ∣ ∣ i = 0 ∑ n − 1 f ( t i ) ( x i + 1 − x i ) − S ∣ ∣ ∣ ∣ ∣ < ϵ .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Calvin I was taught that if f : ( a , b ] → R is Riemann integrable for all interval [x,b] with a < x < b . In this case, if there exists the limit x → a , x > a lim ∫ x b f ( t ) d t and the limit is finite , then the impropial (Riemann) integral ∫ a b f ( t ) d t converges and the value of this integral is the value of this limit....
Log in to reply
It's an improper integral, which is the limit of Riemann integrable functions. The function isn't Riemann integrable. Quoting from Wikipedia ,
Often one is able to compute values for improper integrals, even when the function is not integrable in the conventional sense (as a Riemann integral, for instance) because of a singularity in the function or because one of the bounds of integration is infinite... The narrow definition of the Riemann integral also does not cover the function 1 / x on the interval [ 0 , 1 ] . The problem here is that the integrand is unbounded in the domain of integration (the definition requires that both the domain of integration and the integrand be bounded). However, the improper integral does exist if understood as the limit.
We have to be careful with the conditions of the theorems under which we can apply them. For example (but not a perfect example), quoting from Ruidin's Principle of Mathematical Analysis,
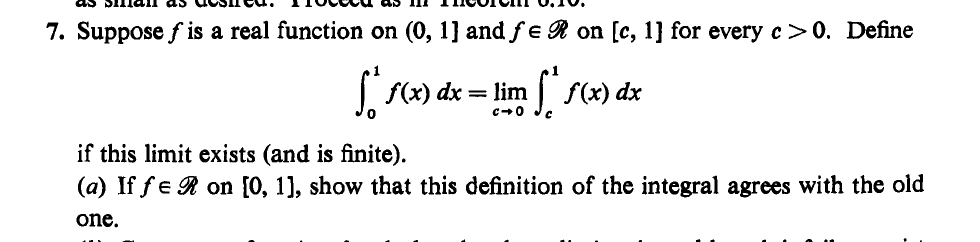
we see that we need the assumption that f is Riemann integrable, which again requires that f is bounded (on the closed interval [ 0 , 1 ] ).
It is because of reasons like this (and more), that we abandon the Riemann integral in favor of the Lebesgue integral.
Yes, we are relying on the definitions of these terms and working from first principles in order to understand these terms fully and ensure that we're not using preconceived notions/simplifications/generalizations.
Log in to reply
Ok, I think I'm getting you. But I have still some doubts, for example, consider ϵ > 0 , ϵ ∈ R and ϵ very small. Let's suppose the Riemann integral ∫ ϵ 1 x 1 d x . This integral exists, doesn't it? Let's make the change x = t 2 1 with t > 0 then, applying U- substitution d x = t 3 − 2 d t we get ∫ ϵ 1 x 1 d x = 2 ∫ 1 ϵ 1 t 2 1 d t , don't we? The function f ( t ) = t 2 1 is continuous and bounded in this interval and it's Riemann integrable, then my question is: what can we say about its improper integral in the interval [ 1 , ∞ ) ? Quoting Wikipedia
The problem here is the domain of integration (the definition requires that both the domain of integration and the integrand be bounded). However, the improper integral does exist if understood as the limit
Log in to reply
@Guillermo Templado – The improper integral isn't an actual Riemann integral. From the line "if understood as the limit", that means that "If we attach this additional meaning, we can come up with a (separate) theory that extends what we've done in this particular scenario. However, we still have to check if all the previous conclusions apply to this scenario".
As a somewhat similar definition, we can add the symbol ∞ into addition and multiplication of complex numbers, and it could have the (seperate) theory that ∞ + x = ∞ and ∞ × x = ∞ . However, we have to check various precious conclusions, and we realize that ∞ − ∞ doesn't work well in the associative / commutative system that we've created.
Log in to reply
@Calvin Lin – ∞ − ∞ is indetermined or it depends where we are (for example, if we are in a complexion of the complex plane, sorry I don't know what is the exact word in English...) It's clear for me, but this is not the case. I know also a lot of times many considerations depend on agreements. Is this the case here? This is my question, I think only we can consider this integral asking about its Riemann integral as an improper Riemann integral, because it's impossible consider this Riemann integral as proper, due to your previous arguments...
Log in to reply
@Guillermo Templado – As I said,
Now, let's see why the bounded criteria is necessary in the theorem, by working from first principles of the Riemann integral.
Using the definition of the Riemann integral, this function isn't integrable. If you have an alternative definition (through a reputable source), you can also verify that unbounded functions are not Riemann integrable.
I believe that the "agreement" of the definition is consistent in the mathematical community, but it could be that internationally some countries deal with it differently (E.g. "positive" is "non-negative" in some places). If this were the case, please let me know.
Log in to reply
@Calvin Lin – Give me some time , please, I'm a bit lost right now and I need to meditate. I think the problem is: you consider this Riemann integral from a point of view distinct to mine, from first principles,integrand bounded and compact, etc... and I consider this Riemann integral as an improper Riemann integral and I have a meaning of this like a limit, and this is not the case, I think... Please, give me some time to meditate your words and your proof...
Log in to reply
@Guillermo Templado – That is indeed the point of my question. "I know that most of you chose the answer of 2, because that was what your teacher told you." For those who do not have a firm grasp of the definition, they might think that the Riemann integral exists.
Here's a better analogy in calculus. Many people learnt continuous functions are those that "you can just draw with your pen without lifting it up from the paper". It seems to work well in high school, where every continuous / discontinuous function that they see obeys that property, and school teachers do not bother to dissuade that idea because it helps them avoid a thorny discussion (and makes the intermediate value theorem proof immediate). However, the students learn the proper approach through epsilon-delta definition of a limit , not many would realize that this claim is false. This in turn hampers them in understanding the proof of intermediate value theorem and why it's much more complex than "Well, clearly the pen must cross this line". (I see that we only have the "intuitive proof", instead of a proper rigorous proof. Will make a note to improve this page)
So yes, sometimes intuition is helpful, and we can say "Well, most of the time this works". However, we also have to be careful with when it fails, and ensure that it doesn't impact anything else we're doing.
Log in to reply
@Calvin Lin – I agree, you are completely right here.
Log in to reply
@Guillermo Templado – Calvin, whith this definition of Riemann- integral the answer is right.... But there are more than 10000 problems on Brilliant than are using the improper integral Riemann. Then, what do we have to do? Following this definition? or being answered the question as a limit?( what is the general case)? Do you want examples...?
Can you evaluate the exact form of this definite integral?
What integral is he using?... (lebesgue integral, improper Riemann integral, Riemann Stieljes...?
Practice: a nice definite integral.
Log in to reply
@Guillermo Templado – As always, problems have to be interpreted from the proper context. When no context is provided, we assume that it's the typical general context. In the 2 problems that you provided, since no context is given we take the context in which the integrals make sense, which would be the improper riemann integral or the lebesgue integral.
However, if context is given, e.g. "Riemann integral" in this case, or "take the zeta-regularization value" or "evaluate in base 8...", then we have to answer accordingly.
Log in to reply
@Calvin Lin – ok, in this case, then all is just clear for me... Only, good, this problem originally didn't have the definition, ok it's equal...
The limit does not exist (solved this on my phone, and it moved to the wrong answer. It's not continuous at 0. and does not follow Reimann definition of an integral.
Log in to reply
Not being continuous at 0 isn't a sufficient reason for the Reimann integral not existing. The explanation has to be more detailed than that.
E.g. the function f ( x ) = 1 when x = 0 and f ( x ) = x for 0 < x ≤ 1 is Riemann integrable.
I know that most of you chose the answer of 2, because that was what your teacher told you. Specifically, that
∫ 0 1 x 1 d x = [ 2 x ] 0 1 = 2
However, you are not performing the Riemann integral when you evaluate this way! The Riemann-Lebesgue theorem states that
I know that most of you learnt that the riemann sums is calculated as a left sum and as a right sum, and if the sums converge then the Riemann integral exists. However, they neglected to explain the criteria under which we only need to consider left and right sums. There are various criteria on the functions, like having a bounded+continuous function, or having a monotonic function on a compact interval.
As an explicit example, we know that the function
f ( x ) = { 0 1 x ∈ Q x ∈ Q is not Riemann-integrable. However, if we simply took the intervals with endpoints n k , we would calculate that the left and right Riemann sums are always 0. We see that this function is neither bounded+continuous, nor monotonic, and hence we cannot just consider left and right sums.
Similarly, in the case of x 1 , because the function isn't defined at 0, the function isn't continuous at 0. On the other hand, if we tried to fix this by removing 0 from the domain, we do not have a compact interval (even though the function would be monotonic). As such, we once again cannot just consider left and right sums.
Now, let's see why the bounded criteria is necessary in the theorem, by working from first principles of the Riemann integral. The Riemann integral of f equals S if the following condition holds:
If the function is unbounded and tends to (positive) infinity at the point p = 0 , then given any partition, we can always find a sequence of tags such that x i ≤ p ≤ x i + 1 and t i n with t i n → + ∞ . With this sequence of tags, we see that ∑ i = 0 i = n − 1 f ( t i ) ( x i + 1 − x i ) is unbounded, and thus the Riemannian integrability condition cannot hold. Thus, all unbounded functions are not Riemann-integrable.
The entire Riemann-Lebesgue theorem takes a bit more machinery to prove. Give it a shot!
Note: For those people who try and justify the initial equation using the fundamental theorem of calculus , once again we have to note the conditions under which the theorem holds. In particular, we need that f is continuous on the closed interval [ a , b ] , which isn't true for x 1 as it is not defined at x = 0 , and removing that point leaves us an open interval (which is not compact).