Inspired by Inspired by Inspired by π han
Let f ( x ) denote a 7 th degree polynomial satisfying f n = 3 n for n = 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 . Find f ( 8 ) .
Inspirations : First link , Second link , Third link .
The answer is 6305.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Nice! So can we deduce a general form for this? My method was by method of differences.
Log in to reply
I hesitate to call the method "general", but it is an option when fitting a polynomial to exponential data points.
Same, even I used the method of differences.
But i see that the equation you have is not a polynomial one expansion of (1+2)^x so how does this satisfy the question
This was a long time ago, but what exactly is this motivation for coming up with that polynomial?
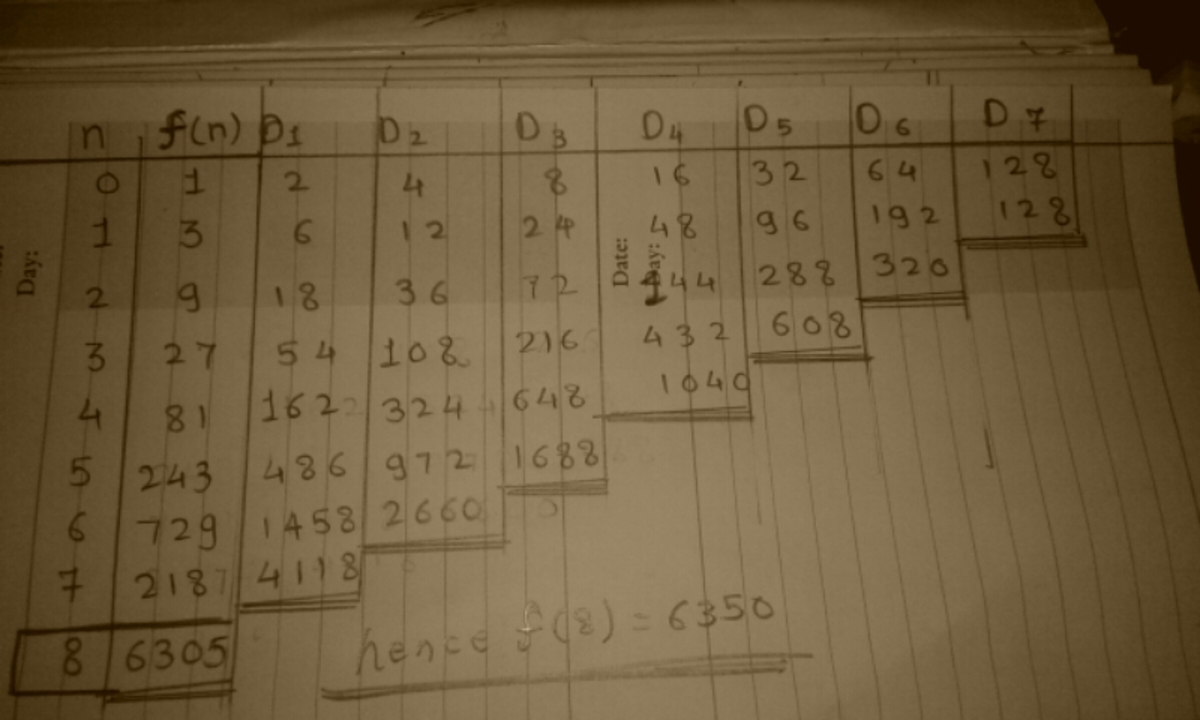
I used method of differences It is rather longer method though...
Even I used the same :-P
PS-Why don't you display it in L A T E X ?
Log in to reply
I want to show of my nice handwriting hahahaha...
I dont know how to make a diff.table in latex bro...
Log in to reply
OK ! See my solution on this problem.
Log in to reply
@Akshat Sharda – Ah , I can do toggle latex now thanks !!!
'#'SuchMehnat
Log in to reply
Haha , It took me nearly 20 min to draw this table ,,,
MOD is really amazing theorem.
Cheap solution here.
By the Super Automatic Regressionator v1.1.2 , setting 8 points to (0, 1), (1, 3) etc. gives L(x) and L(8) happens to be 6305.
I'm glad I made that stupid calculator >.>
s̶t̶u̶p̶i̶d̶ efficient calculator
I found a veeery weird solution using table of differences... I don't know why it works, though...
The sum is also equal to i = 0 ∑ 7 3 i 2 7 − i = 6 3 0 5
You have got Eagle's eye.....:D
Yes, good observation! You can see that our solutions are the same since 3 8 − 2 8 = ( 3 − 2 ) ∑ i = 0 7 3 i 2 7 − i
Log in to reply
Here is my solution , neatly made Table of differences , in my best handwriting...
Let f ( x ) = ∑ k = 0 7 2 k ( k x ) and find f ( 8 ) = 3 8 − 2 8 = 6 3 0 5