Tricky Congruence

$a^x \equiv a-2 (mod (a-1)) \\ \Rightarrow \exists\ n \in \mathbb{Z}: a^x = n(a-1) + a - 2 \\ \Rightarrow n = \frac{a^x - a + 2}{a-1}$

Since $a^n - b^n = (a - b)(a^{n-1}+a^{n-2}b+a^{n-3}b^2+\cdots+ab^{n-2}+b^{n-1})$ , we know that $a^x - 1^x = (a - 1)(a^{x-1}+a^{x-2}+a^{x-3}+...+1)$ .

Thus, $n = \frac{(a^x - 1) - a + 3}{a - 1} = (a^{x-1}+a^{x-2}+a^{x-3}+...+1) - \frac{a - 3}{a - 1}$ .

Since n is an integer, and all the other terms are integers, we know that $\frac{a - 3}{a - 1}$ is also an integer.

We know that $a \gt 2$ , and if $a \gt 3$ , our denominator would exceed our numerator, and we could never get an integer.

At $a = 3$ , $\frac{a - 3}{a - 1} = 0$ , providing a valid value of n. Thus, $a = 3$ . QED.

Let $b:=a-1\geq2$ , then the equality reads $(b+1)^x\equiv b-1\pmod{b}\iff 1^x\equiv-1\pmod{b}\iff 2\equiv 0\pmod{b}.$ This means that $b|2$ , so necessarily $b=2$ . Therefore, $a=3$ .

$a^x\equiv a-2 \equiv -1 \pmod{a-1}\\ \Longrightarrow a^x+1\equiv 0 \pmod{a-1}\\ \Longrightarrow \dfrac{a^x+1}{a-1}\text{is and integer}\\ a^x\equiv 1\pmod{a-1}\\ \Longrightarrow a^x+1\equiv 2\pmod{a-1}\\ \Longrightarrow (a-1)|2\\ a=3$ .

a congruent to 1 ( mod a-1 )

a^x congruent to 1^x (mod a-1)

hence 1=a-2

so a=3

We know $\begin{aligned} a & \equiv 1\ \textrm{mod}\ (a-1)\\ \Rightarrow a^{x} & \equiv 1^{x}\ \textrm{mod}\ (a-1) \end{aligned}$ for all positive integers $x$ , and $\begin{aligned} a-2 & \equiv -1 \textrm{ mod}\ (a-1). \end{aligned}$ So the equation above reads $\begin{aligned} 1 & \equiv -1 \textrm{ mod}\ (a-1) \end{aligned}$ or $\begin{aligned} 2 & \equiv 0 \textrm{ mod}\ (a-1). \end{aligned}$ This means $2$ is divisible by $a-1$ , which is only true for $\boxed{a= 3}$ if we assume $a>2$ .

Subtracting 1 from both sides does not defy the congruence: $a^x-1 \equiv a-3 \pmod{(a-1)}$ Now, since $(a-1)$ is a factor of $(a^x-1^x)$ : $a-3 \mod{(a-1)} = 0$ This implies that $a - 3$ is congruent to $a - 1$ itself , since $a - 1 \mod{(a-1)} = 0$ . It is clear then that the system cycles over a modulus of 2.

$a-1 = 2$ $\boxed{a=3}$

We notice " $a\equiv 1\mod a-1$ " to simplify the congruence: $\begin{aligned} 1&\equiv 1^x\equiv a^x\equiv a-2\equiv 1-2\equiv -1\mod a-1&&&\Leftrightarrow &&&& 2=1-(-1)&\overset{!}{=}k(a-1),&k\in\mathbb{Z} \end{aligned}$ We find $a-1$ must divide $2$ , that is $a-1\in\{\pm1;\:\pm2\}$ . With $a>2$ , we only have one solution $a=\boxed{3}$

Since nothing is mentioned about x except x >2 ,lets take a special case of x=3.Now according to question, a^3-a+2 must be perfectly divisible by (a-1) .So go for long division.2 will come at last and hence (a-1) must be 2 for a perfect division.Thus a=3!!!!

Just ask yourself, : "" Hmm, this looks like it could be Fermat's Little Theorem. What would be needed for it is be so ? "" Well, the right needs to equal 1.

Then you'll notice that the right side equals 1 if a = 3.

Then you will also notice that the modulus will equal 3 -1 = 2. So this means that P = 2.

Then you will also notice since x must be the same as P-1 , it means that x = 1. So we also got x !

Then we confirm this by noticing that

3^1 - 1 = 2. which gives an integer when divided by the modulus 2.

Done !

• a^x is congruent to a-2 modulo (a-1)
• a^x=-1 modulo(a-1)
• a^x+1=0 modulo (a-1)
• 1 + 1=0 modulo(a-1)
• since a=1 modulo(a-1)
• 2=0 modulo(a-1)
• Therefore a-1 divides 2.
• either a-1=1 (which gives a=2) or a-1=2(which gives a=3)
• but it is given a and x are greater than 2.
• Thus,The only solution is a=3.

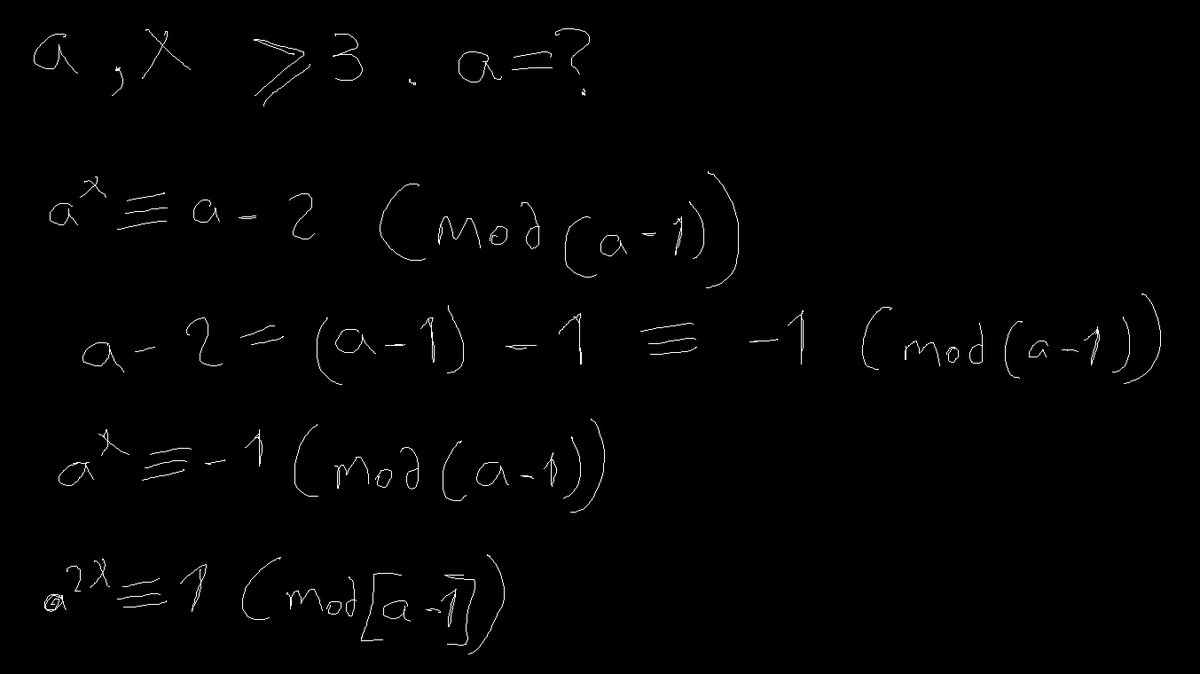
I didn't something wrong and ended with an equation that validate (a) to be any integer I just want to understand my mistake, would someone tell me where is the wrong step? and why?