AP/GP

$\begin{array}{lrll} \text{We know that } & \dfrac{1}{1-x} & = 1 + x + x^2 + x^3 + x^4 + x^5 + ... & \text{for } -1 < x < 1 \\ \text{Differentiate both sides } & \dfrac{1}{(1-x)^2} & = 1 + 2x + 3x^2 + 4x^3 + 5x^4 + ... \\ \text{Differentiate again } & \dfrac{2}{(1-x)^3} & = 1\times 2 + 2\times 3x + 3\times 4x^2 + 4\times 5x^3 + ... \\ \text{Multiplied by }x & \dfrac{2x}{(1-x)^3} & = 1\times 2x + 2\times 3x^2 + 3\times 4x^3 + 4\times 5x^4 + ... \\ \text{Let }x = \dfrac{1}{10} < 1 & \dfrac{\frac{2}{10}}{\left(1-\frac{1}{10}\right) ^3} & = \dfrac{1\times 2}{10} + \dfrac{2\times 3}{10^2} + \dfrac{3\times 4}{10^3} + \dfrac{4\times 5}{10^4} + ... \\ & & = \dfrac{200}{729} \end{array}$

$\Rightarrow A + B = \boxed{929}$

A non-calculus approach,

Let, $S=\frac { 1\times 2 }{ 10 } +\frac { 2\times 3 }{ { 10 }^{ 2 } } +\frac { 3\times 4 }{ { 10 }^{ 3 } } +\frac { 4\times 5 }{ { 10 }^{ 4 } } ....................\infty \quad \quad -------\quad (1)\\ \Rightarrow \frac { S }{ 10 } =\frac { 1\times 2 }{ { 10 }^{ 2 } } +\frac { 2\times 3 }{ { 10 }^{ 3 } } +\frac { 3\times 4 }{ { 10 }^{ 4 } } +\frac { 4\times 5 }{ { 10 }^{ 5 } } ....................\infty \quad \quad \quad --------(2)\\ Subtracting\quad (1)\quad from\quad (2),\\ \\ \frac { 9S }{ 10 } =\frac { 1\times 2 }{ 10 } +\frac { 2\times 2 }{ { 10 }^{ 2 } } +\frac { 3\times 2 }{ { 10 }^{ 3 } } +\frac { 4\times 2 }{ { 10 }^{ 4 } } ....................\infty \\ \Rightarrow \frac { 9S }{ 20 } =\frac { 1 }{ 10 } +\frac { 2 }{ { 10 }^{ 2 } } +\frac { 3 }{ { 10 }^{ 3 } } +\frac { 4 }{ { 10 }^{ 4 } } ....................\infty \quad --------(3)\\ \Rightarrow \frac { 9S }{ 200 } =\frac { 1 }{ { 10 }^{ 2 } } +\frac { 2 }{ { 10 }^{ 3 } } +\frac { 3 }{ { 10 }^{ 4 } } +\frac { 4 }{ { 10 }^{ 5 } } ....................\infty \quad \quad \quad --------(4)\\ Again\quad Subtracting\quad (3)\quad from\quad (4),\\ \frac { 81S }{ 200 } =\frac { 1 }{ 10 } +\frac { 1 }{ { 10 }^{ 2 } } +\frac { 1 }{ { 10 }^{ 3 } } +\frac { 1 }{ { 10 }^{ 4 } } .................\infty \quad =\frac { \frac { 1 }{ 10 } }{ 1-\frac { 1 }{ 10 } } =\frac { 1 }{ 9 } \\ \therefore \quad S=\frac { 200 }{ 729 } =\frac { A }{ B } \\ \\ Therefore\quad A+B= \fbox{929}$

By binomial expansion,

$\left(1-x \right)^{-3} = 1 + \binom{3}{1} x + \binom{4}{2}x^2 + \binom{5}{3}x^3 + \ldots$

$2 \left(1-x \right)^{-3} = 1 \times 2 +2 \binom{3}{1} x +2 \binom{4}{2}x^2 + 2 \binom{5}{3}x^3 + \ldots$

$2 \left(1-x \right)^{-3} = 1 \times 2 +2 \times 3 x +3 \times 4 x^2 + 4 \times 5 x^3 + \ldots$

$2 x \left(1-x \right)^{-3} = 1 \times 2x +2 \times 3 x^2 +3 \times 4 x^3 + 4 \times 5 x^4 + \ldots$

Taking $x= \dfrac{1}{10}$ . We get,

$\dfrac{1 \times 2}{10} + \dfrac{2 \times 3}{10^2} + \dfrac{3 \times 4}{10^3} + \dfrac{4 \times 5}{10^4} + \ldots = 2 \times \dfrac{1}{10} \times \dfrac{1}{1- \left( \dfrac{1}{10} \right) ^3} = \dfrac{200}{729}$

Therefore, $a=200$ and $b=729$ . $\boxed{a+b = 929}$ .

---

Using Calculus:

Since $1+x+ x^2 +x^3 + x^4 + \ldots = \dfrac{1}{1-x}$

Differentiate it w.r.t $x$ ,

$1+ 2x + 3x^2 + 4x^3 +5 x^4 + \ldots = \dfrac{1}{\left(1-x \right)^2}$

Differentiate it again w.r.t $x$ ,

$1 \times 2 + 2\times 3 x + 3 \times 4 x^2 + 4 \times 5 x^3 + \ldots = \dfrac{2}{\left( 1-x \right)^3}$

Multiplying with $x$ on both sides, we get

$1 \times 2x +2 \times 3 x^2 +3 \times 4 x^3 + 4 \times 5 x^4 + \ldots = \dfrac{2x}{\left(1-x \right)^3}$

Taking $x=\dfrac{1}{10}$ .

$\dfrac{1 \times 2}{10} + \dfrac{2 \times 3}{10^2} + \dfrac{3 \times 4}{10^3} + \dfrac{4 \times 5}{10^4} + \ldots = 2 \times \dfrac{1}{10} \times \dfrac{1}{1- \left( \dfrac{1}{10} \right) ^3} = \dfrac{200}{729}$

Therefore, $a=200$ and $b=729$ . $\boxed{a+b = 929}$ .

Another solution employing differentiation: Let $f(x) = \sum_{n=1}^\infty n(n+1)x^{n-1},$ then the required value is equal to $\tfrac1{10}\ f(\tfrac1{10})$ .

Now $f(x) = \sum_{n=1}^\infty n(n+1)x^{n-1} = \sum_{n=1}^\infty \frac{d^2}{dx^2} x^{n+1} = \frac{d^2}{dx^2} \sum_{n=1}^\infty x^{n+1} \\ = \frac{d^2}{dx^2} \frac{x^2}{1-x} = \frac{d}{dx} \frac{2x-x^2}{(1-x)^2} = \frac{d}{dx} \left(1-\frac{1}{(1-x)^2}\right) = \frac{2}{(1-x)^3};$ therefore $\tfrac1{10}\ f(\tfrac1{10}) = \tfrac1{10}\ \frac{2}{(\tfrac9{10})^3} = \frac{2\cdot 10^2}{9^3} = \frac{200}{729}.$ Thus the answer is $200 + 729 = \boxed{929}$ .

'Alternatively'.

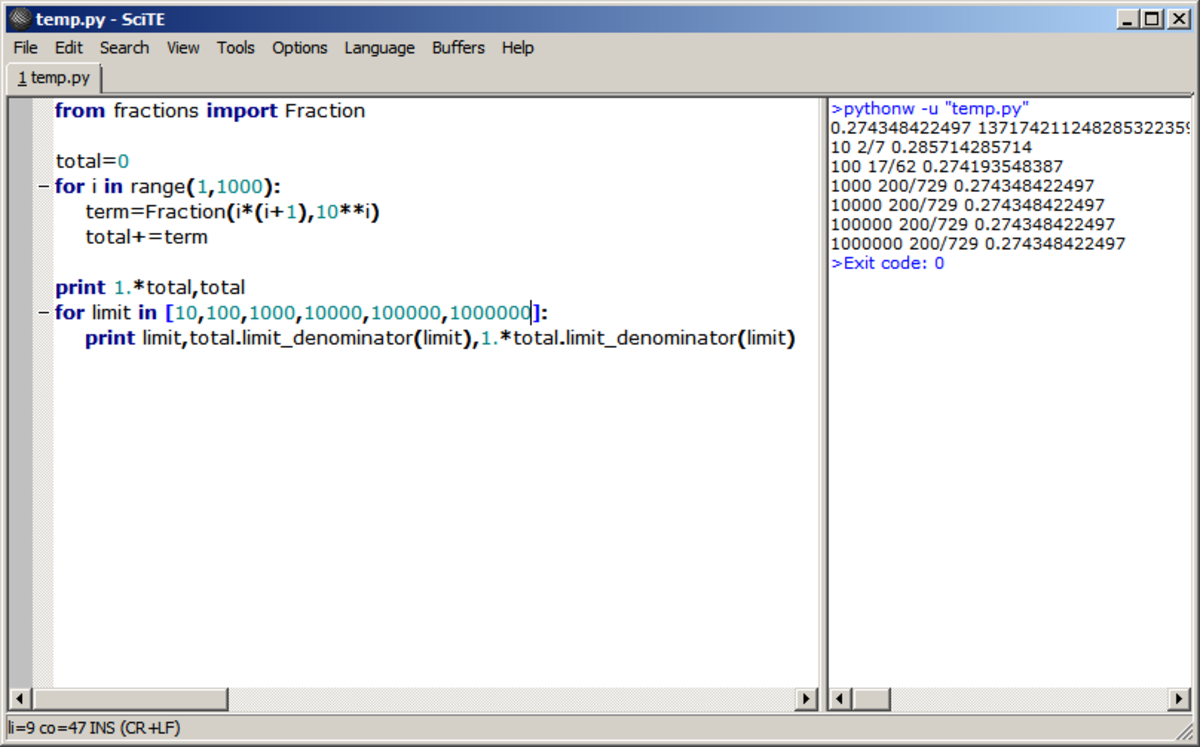
limit_denominator finds the nearest fraction to a given fraction limiting the denominator to the value of its single argument.

Doing by method of shifting of summation

=2×1/10+2×(1+2)/10²+2×(1+2+3)/10³+...=2×((1/10+1/10²+1/10³+...)+2(2/10²+2/10³+2/10⁴+...)+...)= 2×(1/10+1/10²+...)×(1+2/10+3/10²+...)= 2×(1/10+1/10²+...)×(1+1/10+1/10²+...)² =2×1/10×(1+1/10+1/10²+...)³= 1/5*(10/9)³=200/729 So A+B=200+729=929